Содержание
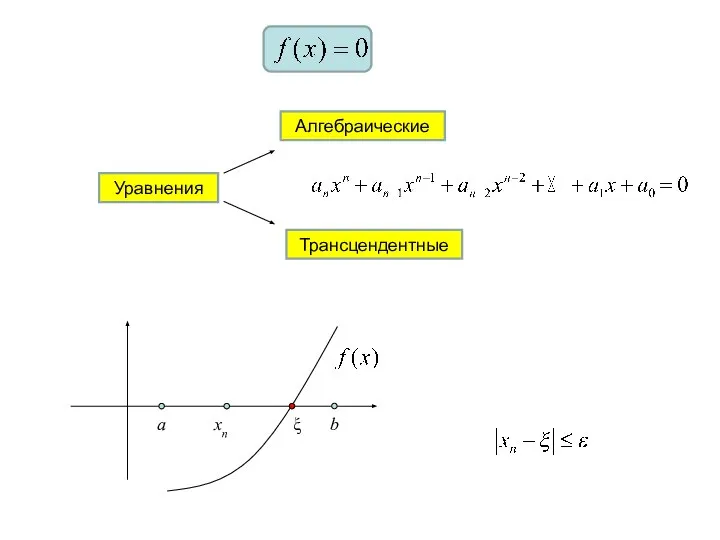
- 2. Уравнения Алгебраические Трансцендентные
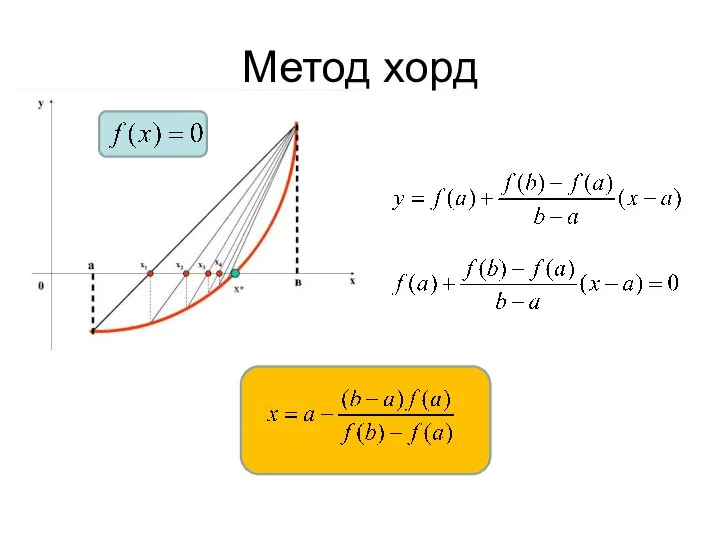
- 3. Метод хорд Метод дихотомии
- 4. Метод хорд Метод хорд
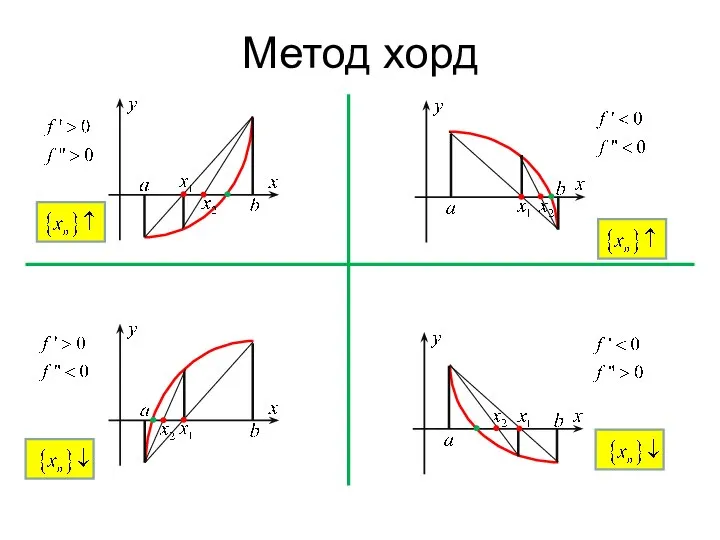
- 5. Метод хорд Метод хорд
- 6. Метод хорд Метод хорд Неподвижная точка в методе хорд – это тот конец отрезка (a или
- 7. Метод хорд Метод хорд
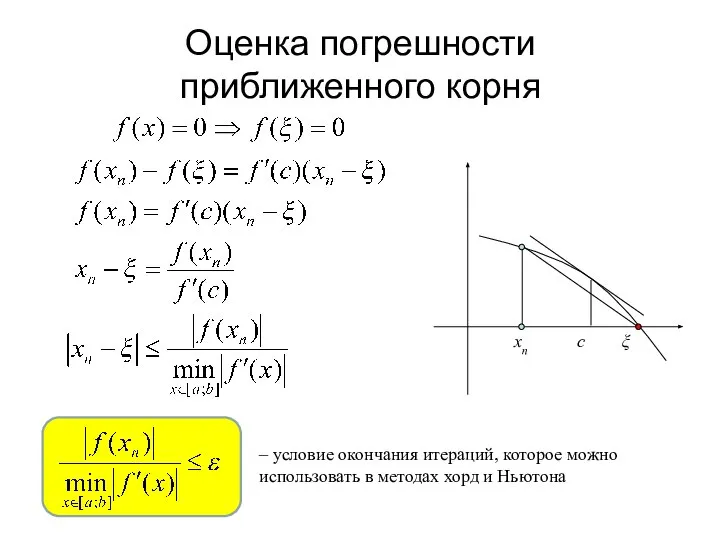
- 8. Оценка погрешности Оценка погрешности приближенного корня – условие окончания итераций, которое можно использовать в методах хорд
- 9. Оценка погрешности Метод хорд оценка погрешности
- 10. Метод хорд (пример) Функция строго возрастает и выпукла вниз на всей числовой прямой. Метод хорд (пример)
- 11. Метод хорд (пример) Метод хорд (пример)
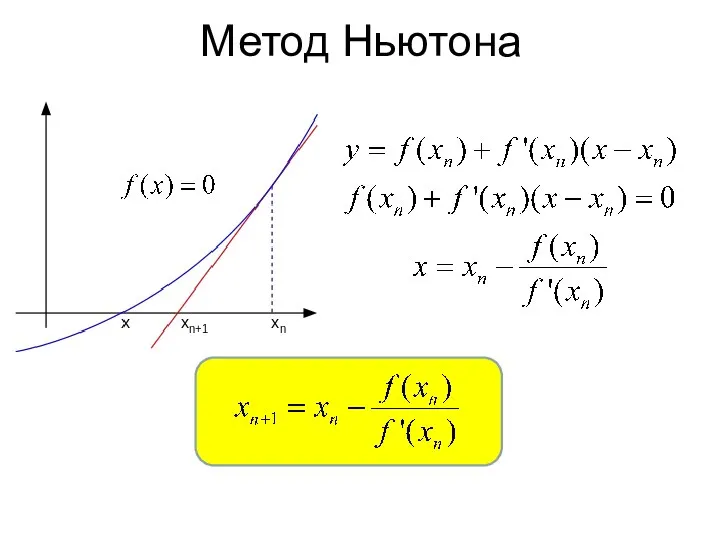
- 12. Метод Ньютона (метод касательных) Метод Ньютона
- 13. Метод Ньютона (метод касательных) Метод Ньютона
- 14. Метод Ньютона (метод касательных) Метод Ньютона
- 15. Оценка погрешности Метод Ньютона
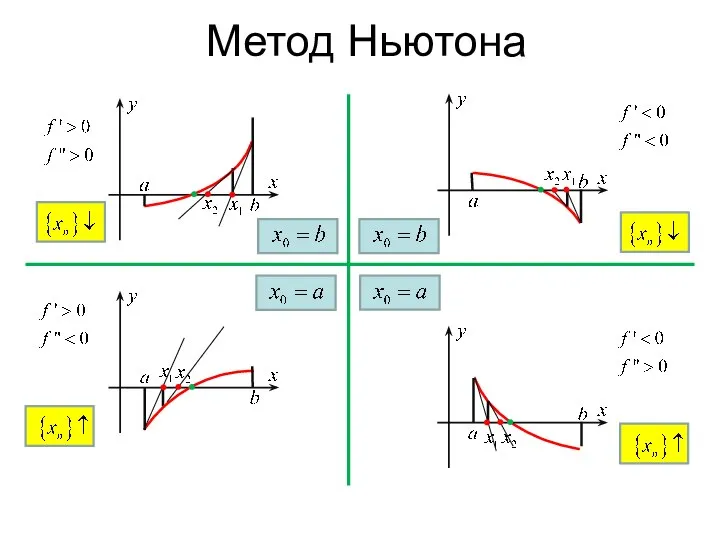
- 16. Метод Ньютона (пример 1) Функция строго возрастает и выпукла вниз на всей числовой прямой. Метод Ньютона
- 17. Метод Ньютона (пример) Метод Ньютона (пример)
- 18. Недостатки: Расходится в тех областях, где 2) если функция f(x) задана таблично, то вычисление затруднено Пути
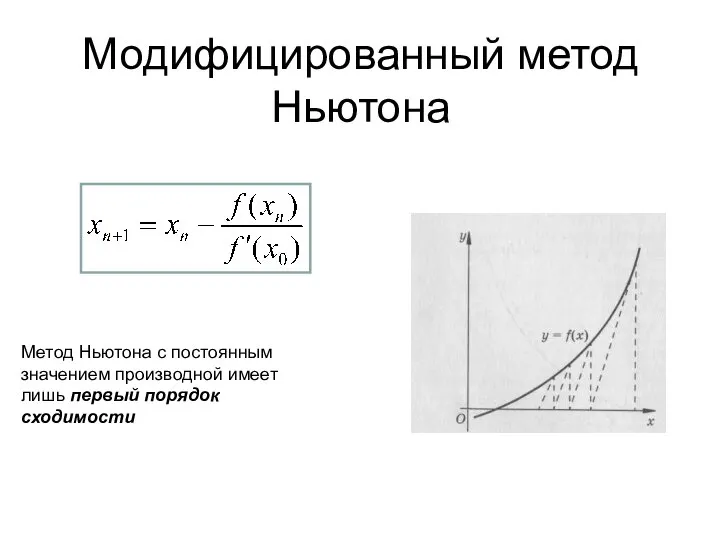
- 19. Метод Ньютона с постоянным значением производной имеет лишь первый порядок сходимости Модифицированный метод Ньютона
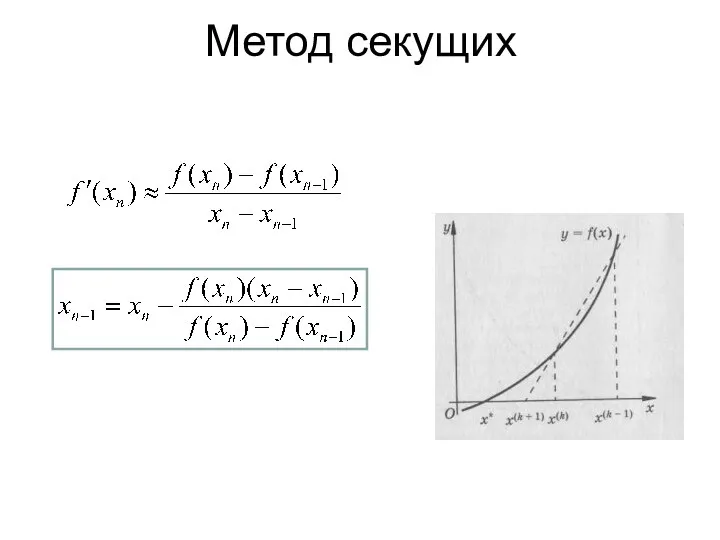
- 20. Метод секущих
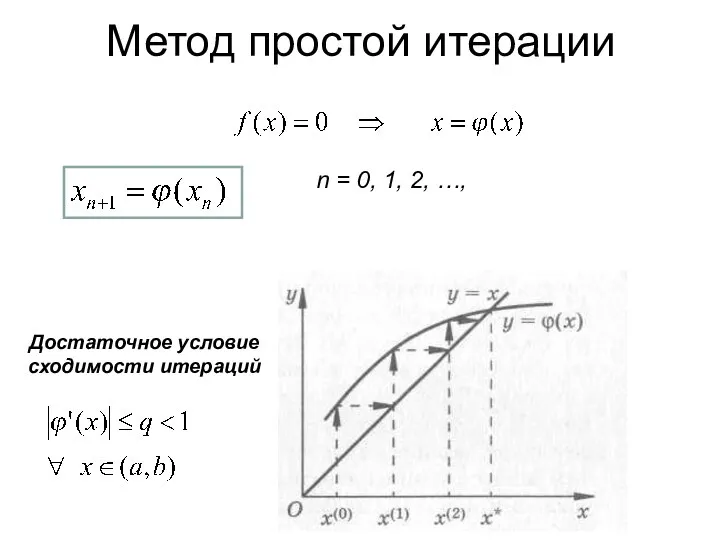
- 21. n = 0, 1, 2, …, Достаточное условие сходимости итераций Метод простой итерации
- 22. Достаточное условие сходимости итераций Метод простой итерации
- 23. Метод простой итерации
- 25. Скачать презентацию













 Решение логических задач с помощью таблиц и метода рассуждений
Решение логических задач с помощью таблиц и метода рассуждений Внеаудиторная самостоятельная работа по теме: Функция, ее свойства и график
Внеаудиторная самостоятельная работа по теме: Функция, ее свойства и график Моделирование. Объекты и их модели. (Тема 10)
Моделирование. Объекты и их модели. (Тема 10) Аттестационная работа. Исследовательская деятельность на уроках математики в 5 классе
Аттестационная работа. Исследовательская деятельность на уроках математики в 5 классе Rinjka liinija
Rinjka liinija Устные приёмы сложения и вычитания в пределах 100. Урок математики во 2 классе
Устные приёмы сложения и вычитания в пределах 100. Урок математики во 2 классе Возведение в куб суммы и разности
Возведение в куб суммы и разности Презентация на тему Статистика и математика
Презентация на тему Статистика и математика  Неравенства. Логарифмические неравенства
Неравенства. Логарифмические неравенства Случайные сигналы и их математические модели
Случайные сигналы и их математические модели Волшебная страна - Геометрия
Волшебная страна - Геометрия Презентация на тему Первообразная 11 класс
Презентация на тему Первообразная 11 класс  Прямоугольный параллелепипед
Прямоугольный параллелепипед Медiана, бiсектриса i висoта трикутника. (7 класс)
Медiана, бiсектриса i висoта трикутника. (7 класс) Карточки-задания по теме Конус. Содержат алгоритм решения
Карточки-задания по теме Конус. Содержат алгоритм решения Теорема, обратная теореме Виета
Теорема, обратная теореме Виета Решение уравнений. Бахчисарайский фонтан
Решение уравнений. Бахчисарайский фонтан Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Деление одночлена на одночлен
Деление одночлена на одночлен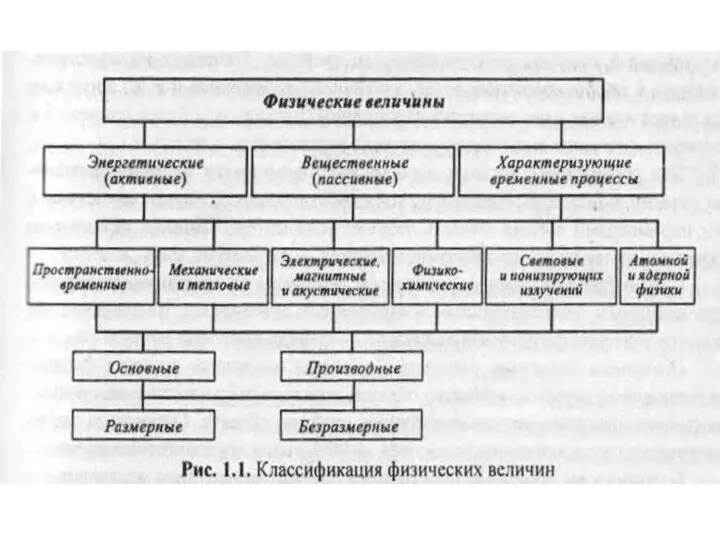 Физические величины
Физические величины Определители матриц
Определители матриц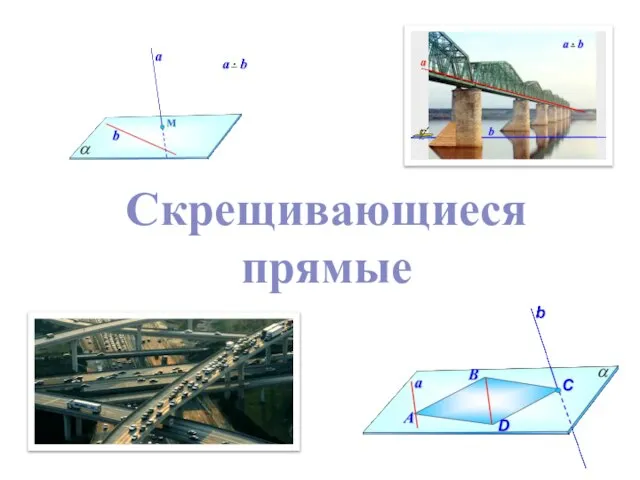 Скрещивающиеся прямые
Скрещивающиеся прямые Алгоритм решения уравнений
Алгоритм решения уравнений Школа волшебников
Школа волшебников Построение фронтальной диметрической и изометрической проекций
Построение фронтальной диметрической и изометрической проекций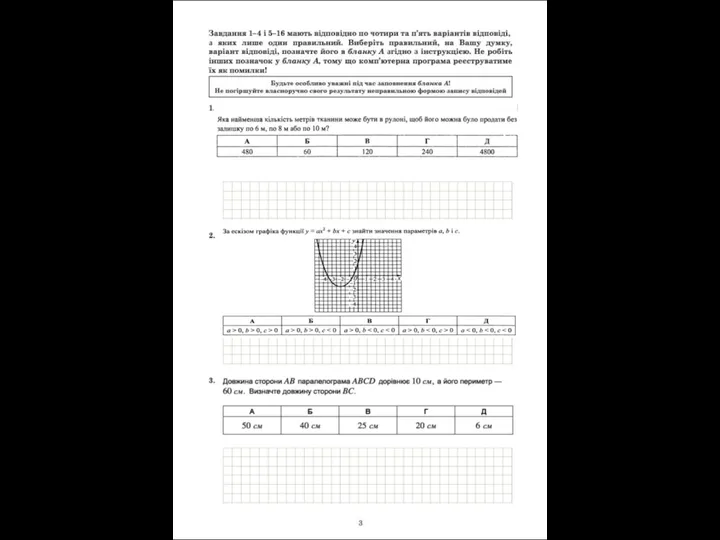 Задания для ЗНО
Задания для ЗНО Число и цифра 9
Число и цифра 9 Точечное оценивание параметров распределений случайных величин
Точечное оценивание параметров распределений случайных величин