Решение систем линейных алгебраических уравнений. Тема 2

Система m линейных уравнений с n переменными имеет вид:
- коэффициенты системы,
- свободные члены.
Решением системы называется такая совокупность значений, при подстановке которых каждое уравнение системы обращается в верное равенство.

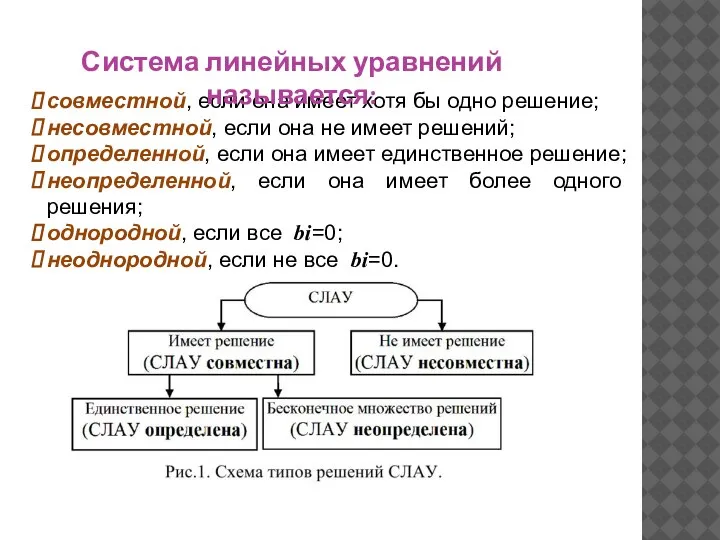
совместной, если она имеет хотя бы одно решение;
несовместной, если она не имеет решений;
определенной, если она имеет единственное решение;
неопределенной, если она имеет более одного решения;
однородной, если все bi=0;
неоднородной, если не все bi=0.
Система линейных уравнений называется:

Рассмотрим систему n линейных уравнений c n неизвестными:
Теорема Крамера:
Пусть Δ - определитель матрицы системы,
Δi - определитель матрицы, получаемой из матрицы A заменой столбца коэффициентов аij при xi столбцом свободных членов.
- формула Крамера.
Тогда, если Δ ≠ 0, то система имеет единственное решение, определяемое по формулам:
Методы решения систем
1. Метод Крамера

Определитель квадратной матрицы – это число, вычисляемое по определённым правилам.
Обозначают: |А|, ΔА, detA .
Вспомним тему: Определители
Боковая
диагональ
Главная
диагональ
Определитель 2-го порядка:

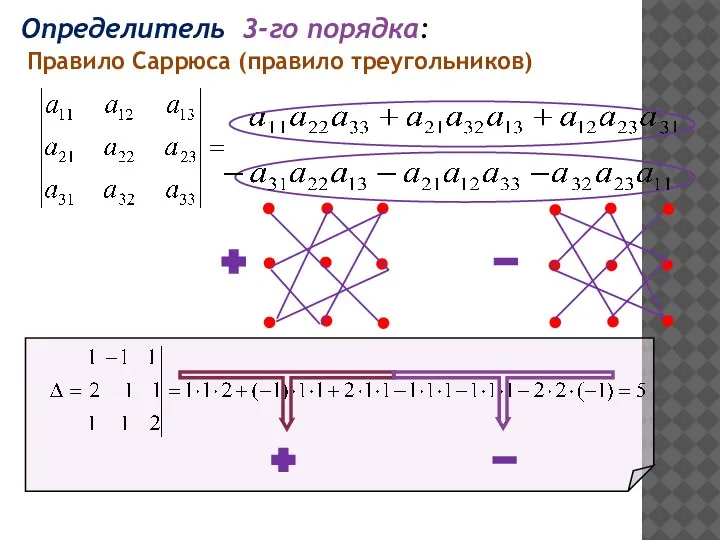
Определитель 3-го порядка:
Правило Саррюса (правило треугольников)

Пример. Решить систему методом Крамера:
3) Подставим полученные значения в формулу Крамера:
Решение. 1)Определитель матрицы системы:
2) Вычислим определители Δ1, Δ2, Δ3 :

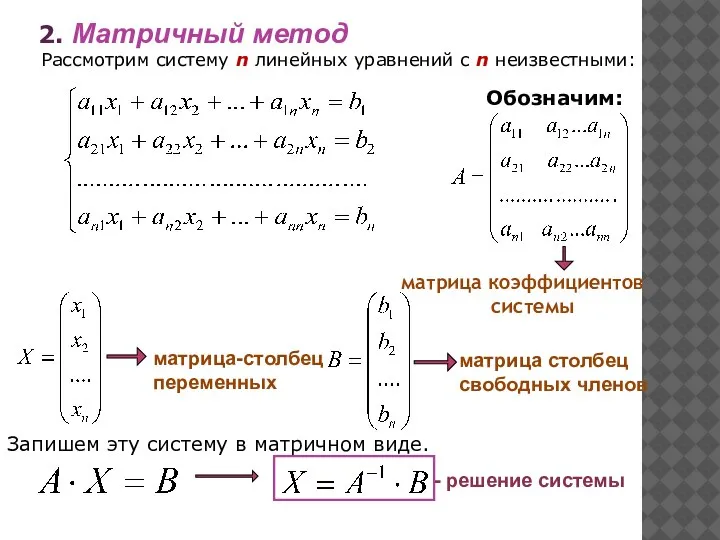
Рассмотрим систему n линейных уравнений c n неизвестными:
матрица коэффициентов
системы
матрица-столбец переменных
матрица столбец свободных членов
решение системы
2. Матричный метод
Запишем эту систему в матричном виде.
Обозначим:

Вывод: число столбцов первого множителя должно
равняться числу строк второго множителя.
Вспомним тему : умножение матриц
Произведением матрицы А размера m x n на матрицу В размера n x k есть матрица С размера m x k , каждый элемент которой вычисляется по формуле:

Пример. Решить систему матричным методом
ОБОЗНАЧИМ
1. Вычислим определитель матрицы

3. Вычисляем обратную матрицу:
4. Проверка:

алгебраические дополнения к элементам строки записаны в столбец
Вспомним тему : Обратная матрица
Матрица А является невырожденной (неособенной), если |А|≠0, иначе матрица называется вырожденной (особенной).
Матрица А-1 называется обратной матрицей к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:

Пример. Найти матрицу обратную к матрице:
Решение.
1. Вычислим определитель матрицы
2. Находим алгебраические дополнения элементов матрицы
определитель матрицы не равен нулю, значит обратная матрица существует

Обратная матрица
2. Найдём алгебраические дополнения элементов матрицы и составим обратную матрицу
3. Решение системы

Рассмотрим систему m линейных уравнений c n неизвестными:
3. Метод Гаусса
- расширенная матрица системы
Цель: с помощью элементарных эквивалентных преобразований получить трапецивидную (треугольную) матрицу

Пример.
Решить систему методом Гаусса
Решение:
Восстановим систему:
Римскими цифрами I, II, III обозначим номера строк системы

ИССЛЕДОВАНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Теорема Кронекера - Капелли. Для того, чтобы система линейных алгебраических уравнений была совместна (имела решение), необходимо и достаточно, чтобы ранг расширенной матрицы системы равнялся рангу матрицы коэффициентов:

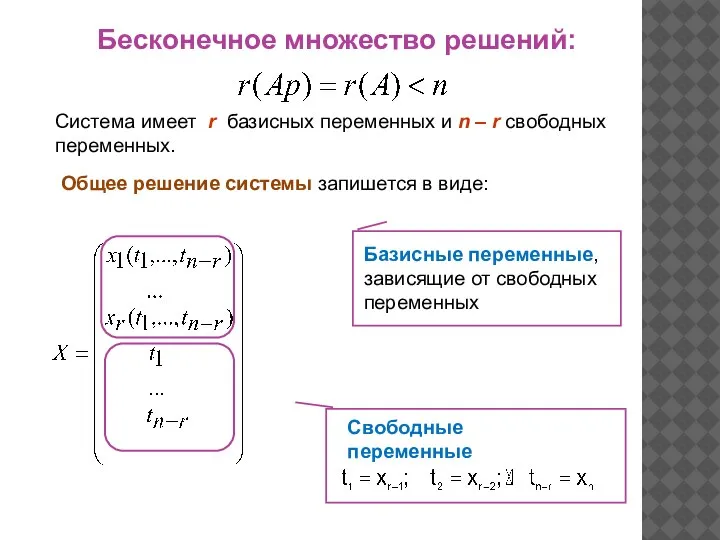
Система имеет r базисных переменных и n – r свободных переменных.
Общее решение системы запишется в виде:
Бесконечное множество решений:

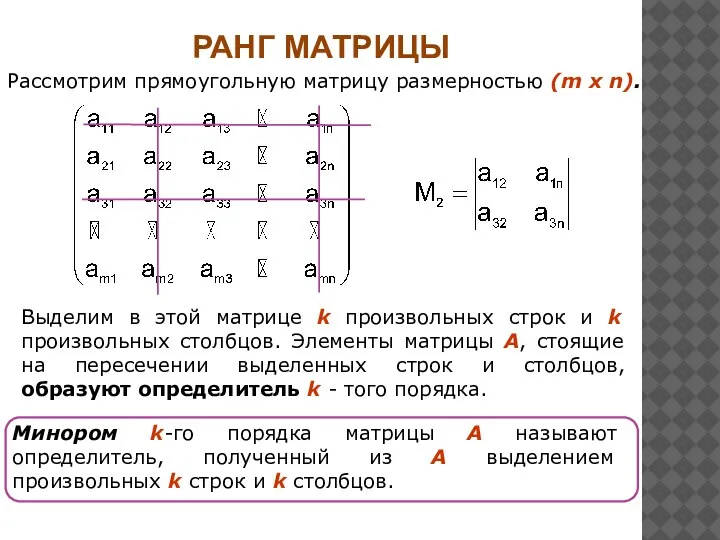
РАНГ МАТРИЦЫ
Рассмотрим прямоугольную матрицу размерностью (m x n).
Выделим в этой матрице k произвольных строк и k произвольных столбцов. Элементы матрицы А, стоящие на пересечении выделенных строк и столбцов, образуют определитель k - того порядка.
Минором k-го порядка матрицы А называют определитель, полученный из А выделением произвольных k строк и k столбцов.

Рангом матрицы называется наибольший порядок отличного от нуля минора этой матрицы.
Матрица А имеет 4 минора 3 - его порядка, например:
18 миноров 2 - го порядка, например:
12 миноров 1 - го порядка – сами элементы.
Наибольший порядок отличного от нуля минора этой матрицы равен 3, поэтому:

Базисным минором называется определитель, порядок которого равен рангу матрицы. Он может быть не единственным.
Теорема.
Эквивалентные преобразования не меняют ранга матрицы.
Умножение или деление элементов одного ряда на одно и то же число, не равное нулю
Перестановка местами двух рядов
Прибавление к элементам ряда элементов другого параллельного ряда, умноженного на произвольный множитель
Эквивалентные преобразования:
Вычеркивание нулевого ряда

Ранг матрицы равен числу ненулевых строк матрицы, приведенной к треугольному виду.
Теорема.
Ранг матрицы равен числу линейно независимых рядов
Два ряда матрицы называются линейно зависимыми, если их линейная комбинация с коэффициентами, не все из которых равны нулю, дает нулевой ряд.
В противном случае ряды называются линейно независимыми.

Решение
совместна
2 базисных переменных, т.к.
неопределенна
1 свободная переменная, т.к.
Восстановим систему:
например,
например,
Пример. Решить систему:

ОДНОРОДНЫЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Однородная система всегда имеет решение:
- тривиальное решение.