Решение уравнений и неравенств заданий С3

МАУ ЗАТО Северск «Ресурсный центр образования»
Консультационный центр по подготовке выпускников к Государственной (итоговой) аттестации
Л.В. Сантьева –учитель математики
Решение уравнений и неравенств
заданий С3
Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа № 196»

МАУ ЗАТО Северск «Ресурсный центр образования»
Спецификация
контрольных измерительных материалов
для проведения в 2013 году единого государственного экзамена по МАТЕМАТИКЕ
Уровень сложности задания С3: П – повышенный
Проверяемые требования (умения): уметь решать уравнения и неравенства
Примерное время выполнения задания учащимся – 30 мин.
Изменения в структуре и содержании экзаменационной работы
2013 г. по сравнению с 2012 г. : без изменения сложности несколько расширена тематика задания С3 – в этом задании может присутствовать система неравенств.
Консультационный центр по подготовке выпускников к Государственной (итоговой) аттестации

МАУ ЗАТО Северск «Ресурсный центр образования»
Консультационный центр по подготовке выпускников к Государственной (итоговой) аттестации
Ответ:
Демонстрационный вариант
контрольных измерительных материалов единого
государственного экзамена 2013 года
по математике
С3 Решите систему неравенств

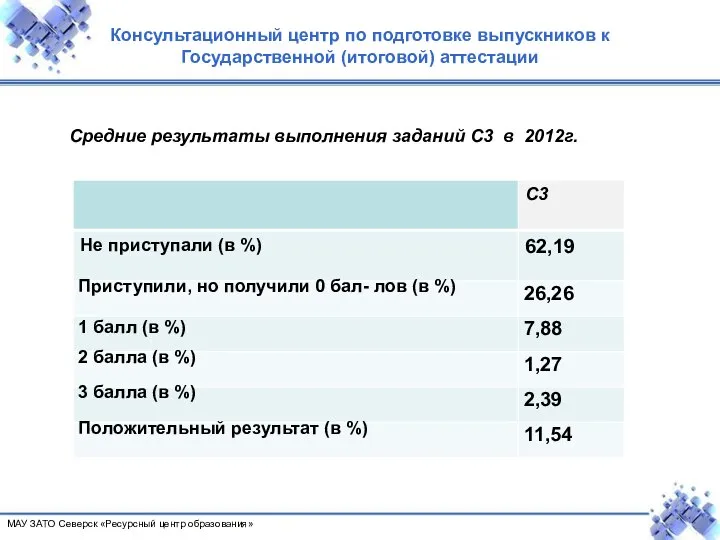
Консультационный центр по подготовке выпускников к Государственной (итоговой) аттестации
МАУ ЗАТО Северск «Ресурсный центр образования»
Средние результаты выполнения заданий С3 в 2012г.

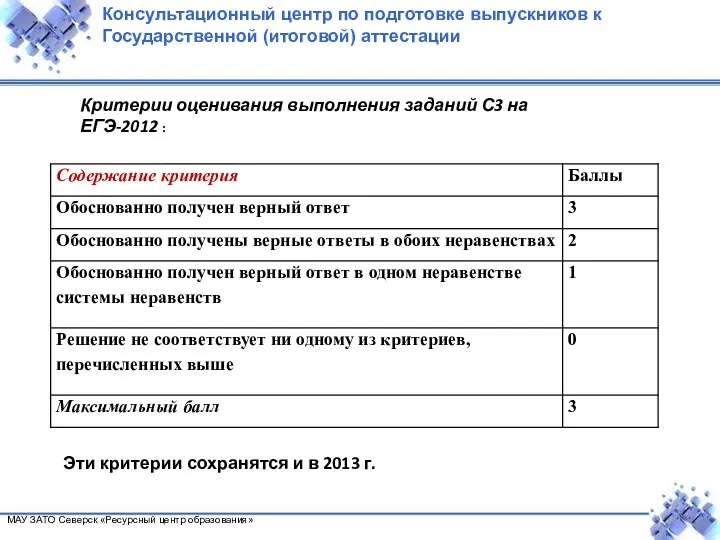
Критерии оценивания выполнения заданий С3 на ЕГЭ-2012 :
Эти критерии сохранятся и в 2013 г.
Консультационный центр по подготовке выпускников к Государственной (итоговой) аттестации
МАУ ЗАТО Северск «Ресурсный центр образования»

Пример 1. С3 Решите систему неравенств
.
Консультационный центр по подготовке выпускников к Государственной (итоговой) аттестации
МАУ ЗАТО Северск «Ресурсный центр образования»

Решение.
Решим первое неравенство системы
Пусть t = , тогда (решений нет) или
Теперь решим неравенство
Итак, решением первого неравенства является множество
Консультационный центр по подготовке выпускников к Государственной (итоговой) аттестации
МАУ ЗАТО Северск «Ресурсный центр образования»

Рассмотрим второе неравенство системы
Найдем ограничения на х:
При следовательно
Для таких значений х рассматриваемое неравенство будет иметь вид:
или
Консультационный центр по подготовке выпускников к Государственной (итоговой) аттестации
МАУ ЗАТО Северск «Ресурсный центр образования»

Пусть , тогда
Решим последнее неравенство методом интервалов. Получим:
т.е.
Решением второго неравенства является множество
Пересечение решений обоих неравенств системы
Ответ:
Консультационный центр по подготовке выпускников к Государственной (итоговой) аттестации
МАУ ЗАТО Северск «Ресурсный центр образования»

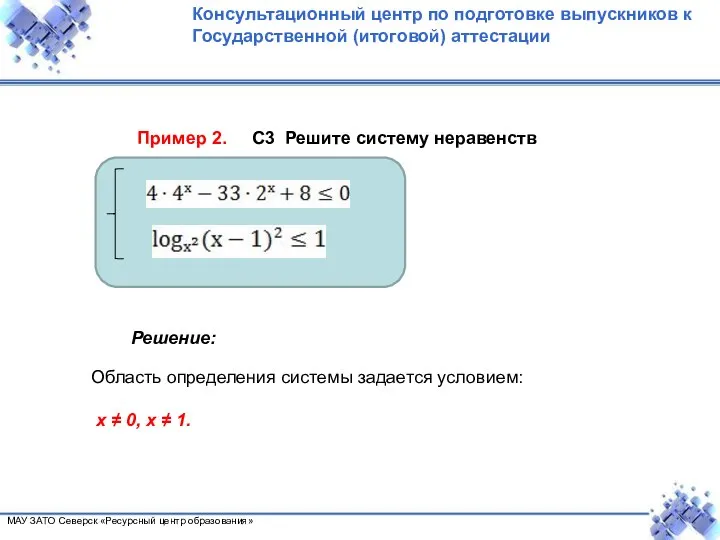
Пример 2. С3 Решите систему неравенств
Решение:
Область определения системы задается условием:
х ≠ 0, х ≠ 1.
Консультационный центр по подготовке выпускников к Государственной (итоговой) аттестации
МАУ ЗАТО Северск «Ресурсный центр образования»

1. Решим первое неравенство системы заменой переменной:
Итак, решением первого неравенства является множество
Консультационный центр по подготовке выпускников к Государственной (итоговой) аттестации
МАУ ЗАТО Северск «Ресурсный центр образования»

2. Рассмотрим второе неравенство
2.1. Пусть
При таком условии исходная система равносильна:
.
Консультационный центр по подготовке выпускников к Государственной (итоговой) аттестации
МАУ ЗАТО Северск «Ресурсный центр образования»

2.2 Пусть .
.
При таком условии исходная система равносильна
3. Объединим решения:
Ответ:
Консультационный центр по подготовке выпускников к Государственной (итоговой) аттестации
МАУ ЗАТО Северск «Ресурсный центр образования»

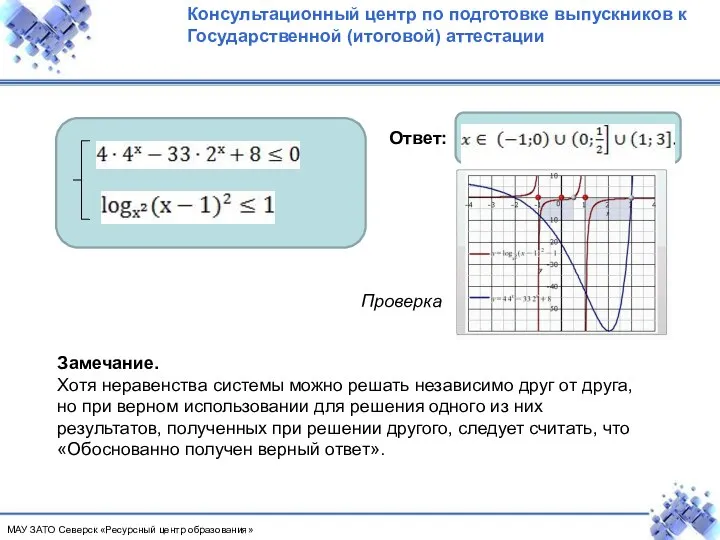
Ответ:
Проверка
Замечание.
Хотя неравенства системы можно решать независимо друг от друга, но при верном использовании для решения одного из них результатов, полученных при решении другого, следует считать, что «Обоснованно получен верный ответ».
Консультационный центр по подготовке выпускников к Государственной (итоговой) аттестации
МАУ ЗАТО Северск «Ресурсный центр образования»

Консультационный центр по подготовке выпускников к Государственной (итоговой) аттестации
Задания для самостоятельного решения:
Ответ:
Ответ :
МАУ ЗАТО Северск «Ресурсный центр образования»