Теория вероятностей и математическая статистика

16.12.2019
Теория вероятностей
Тема 2.
Случайные величины.
Функция распределения и ее свойства. Дискретная случайная величина.
Ряд распределения.
Числовые характеристики.

16.12.2019
Случайные величины
Случайной величиной Х в данном опыте называется переменная величина, которая в результате испытания примет одно из своих возможных значений, но какое именно до проведения опыта неизвестно. Совокупность всех возможных значений случайной величины может быть
Дискретной - все возможные значения случайной величины образуют конечную или бесконечную последовательность (отдельные точечные значения).
Непрерывной - все значения случайной величины заполняют сплошь некоторый промежуток.

16.12.2019
Например,
a) Х - оценка на экзамене
Совокупность значений дискретная -{2,3,4,5}
б) Х - время безотказной работы двигателя (ресурс)
Совокупность значений непрерывная, любое значение из промежутка [0,t] (t - момент отказа двигателя).

16.12.2019
Функция распределения случайной величины
Функцией распределения F(x) случайной величины Х называется вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т.е.
F(x)=P(X
Свойства F(x):
1) область определения F(x) - интервал (-
2) 0 < F(x) ≤ 1,
3) F(-∞)=0, т.к. P(X<- ∞)=P(Θ)=0,
4) F(+∞)=1, т.к. P(X<+ ∞)=P(Ω)=1,
5) F(x)- неубывающая функция.
Будем считать, что F(x) непрерывна слева

16.12.2019
Вероятность попадания случайной величины в промежуток и в точку
Основное свойство функции распределения
Р(α≤X<β)=F(β)-F(α).
Вероятность попадания случайной величины в заданный интервал равна разности значений функции распределения в концах интервала
Следствие:
Р(Х=α) =

16.12.2019
Действительно:

16.12.2019
Дискретная случайная величина
Случайная величина Х называется дискретной, если ее совокупность ее значений дискретна.
Законом (рядом) распределения случайной величины Х называется любая ее вероятностная характеристика, из которой можно получить функцию распределения F(x).

16.12.2019
Законом распределения дискретной случайной величины Х является ряд распределения, т.е. перечисление всех возможных значений Х и их соответствующих вероятностей:
рi=P(X=xi), где i=1;2;...;n;...
Т.к. события (X=x1), (X=x2),...,(X=xn),... образуют полную группу событий и несовместны, то:

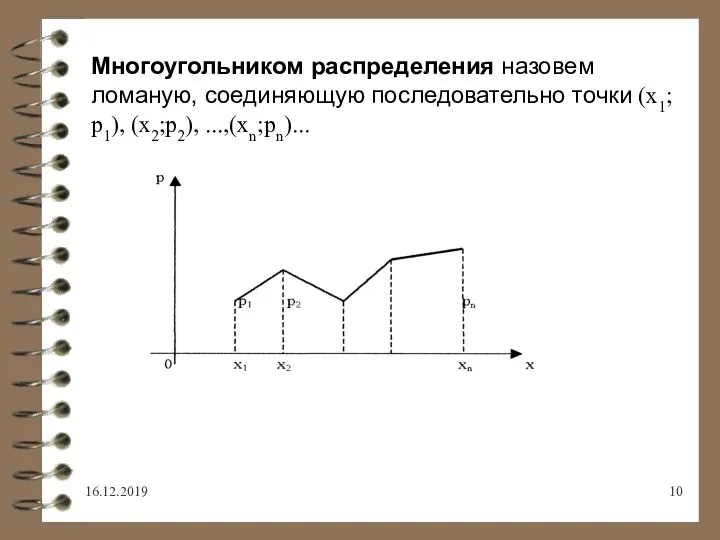
16.12.2019
Многоугольником распределения назовем ломаную, соединяющую последовательно точки (х1;р1), (х2;р2), ...,(хn;рn)...

16.12.2019
Пример 15:
Среди шести микроскопов два изношенных.
Составить ряд распределения случайной величины Х- числа изношенных микроскопов среди трех наудачу отобранных.
Найти функцию распределения F(x) и построить ее график.

16.12.2019
Случайная величина Х может принимать значения: 0;1;2.
Р(Х=0)=
Р(Х=1)=
Р(Х=2)=
Условие нормировки: 0,2+0,6+0,2=1.

16.12.2019
Если x (-∞;0], то F(x)=P(X
если x (0;1], то F(x)=P(X
если x (1;2], то F(x)=P(X
если x (2;+∞), F(x)=P(X
Следовательно,

16.12.2019
Итак,
Зная F(x), можно, например, найти Р(Х=3)=0,
т.к. х=3- точка непрерывности F(x); или найти Р(Х=1)=0,8-0,2=0,6, т.к. х=1- точка разрыва F(x);
или P(-1

16.12.2019
Основные числовые характеристики случайной величины

16.12.2019
Простейшие свойства математического ожидания.
Свойство 1. Математическое ожидание постоянной величины равно самой постоянной, т.е.
М(C)=С.
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания, т.е.
М(СX)=С(MX).
Пример . Дано:
X -3 -1 2
P 0,2 0,5 0,3
Найти М[5X].
Решение.
М[5X]=5M[X], т.к. M[X]=(-3)⋅0,2+(-1)⋅0,5+2⋅0,3=-0,5, то М[5X]=5⋅(-0,5)= -2,5.

16.12.2019

16.12.2019

16.12.2019
Простейшие свойства дисперсии
Свойство 1. Дисперсия постоянной величины равна нулю.
D(C)=0
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат, т.е.
D(СX)=С2(DX).

16.12.2019
Пример . Найти дисперсию случайной величины Х, имеющей следующий закон распределения