Содержание
- 2. Мы уже говорили о том, что различают 3 вида соединений: размещения, перестановки и сочетания. * Логинова
- 3. Как обозначается произведение чисел от 1 до n? Ответ: Произведение всех натуральных чисел от 1 до
- 4. Что называется размещением? По какой формуле вычисляется размещение? Размещениями из n элементов по k называется любой
- 5. На станции 7 запасных путей. Сколькими способами можно расставить на них 4 поезда? * Логинова Н.В.
- 6. Что называется перестановками? Как обозначаются перестановки? По какой формуле вычисляются перестановки? Ответ: Размещения из n элементов
- 7. Что называется сочетаниями? Как обозначаются сочетания и по какой формуле производятся вычисления? Ответ: Сочетаниями из n
- 8. В отличие от размещений в сочетаниях не имеет значения порядок расположения элементов. * Логинова Н.В. МБОУ
- 9. Простейшие комбинации * Логинова Н.В. МБОУ «СОШ №16»
- 10. * Решите задачи: п. 13.5 № 773 Логинова Н.В. МБОУ «СОШ №16»
- 11. В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия
- 12. В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из
- 13. Бригада, занимающаяся ремонтом школы, состоит из 12 маляров и 5 плотников. Из них для ремонта физкультурного
- 14. Задача У одного ученика есть 11 книг по математике, а у другого – 15. Сколькими способами
- 15. Задача У 6 взрослых и 11 детей обнаружены признаки инфекционного заболевания. Чтобы проверить диагноз выбирают 2-х
- 16. Задача В шахматном кружке занимаются 2 девочки и 7 мальчиков. Для участия в соревнованиях необходимо составить
- 17. Задача Сколькими способами можно разбить 10 человек на две баскетбольные команды по 5 человек в каждой?
- 18. Домашнее задание: п. 13.5 № 770, № 774 Задания выполняете к 17.04. * Логинова Н.В. МБОУ
- 20. Скачать презентацию

















 Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях
Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях Методы и приемы решения дробно-рациональных уравнений, содержащих параметр
Методы и приемы решения дробно-рациональных уравнений, содержащих параметр Декартова система координат на плоскости. Математика, 6 класс
Декартова система координат на плоскости. Математика, 6 класс Арифметическая прогрессия в истории
Арифметическая прогрессия в истории Цифровая азбука
Цифровая азбука Теоремы синусов и косинусов
Теоремы синусов и косинусов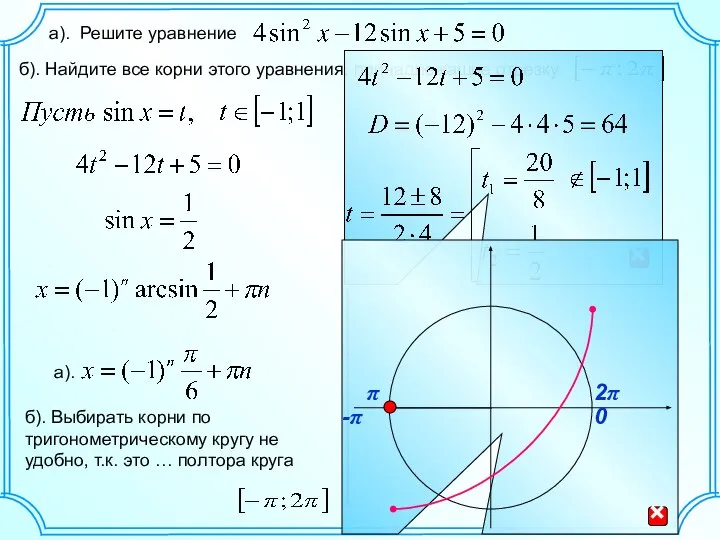 Решение уравнений C 22, по тригонометрии
Решение уравнений C 22, по тригонометрии Закон Ома. Решение задач
Закон Ома. Решение задач Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел
Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел Площадь полной поверхности призмы
Площадь полной поверхности призмы Комбинаторные задачи
Комбинаторные задачи Радианная мера угла
Радианная мера угла Основные тригонометрические тождества. Формулы приведения
Основные тригонометрические тождества. Формулы приведения Vorlesung. Blatt 2
Vorlesung. Blatt 2 Соста числа 11
Соста числа 11 Тригонометрические уравнения
Тригонометрические уравнения Презентация на тему Стандартный вид числа 9 класс
Презентация на тему Стандартный вид числа 9 класс  Лекция 0
Лекция 0 Элементы математической статистики, комбинаторики и теории вероятностей
Элементы математической статистики, комбинаторики и теории вероятностей Презентация на тему Плоскость. Прямая. Луч
Презентация на тему Плоскость. Прямая. Луч  Симметрия. 9 класс
Симметрия. 9 класс Алгоритм Евклида
Алгоритм Евклида Второй и третий признаки равенства треугольников
Второй и третий признаки равенства треугольников Призмы. Виды призм
Призмы. Виды призм Приключения Буратино в Стране Финансов
Приключения Буратино в Стране Финансов Параллелограмм и трапеция. Урок 7
Параллелограмм и трапеция. Урок 7 Периметр и площадь
Периметр и площадь Матрицы и определители
Матрицы и определители