Содержание
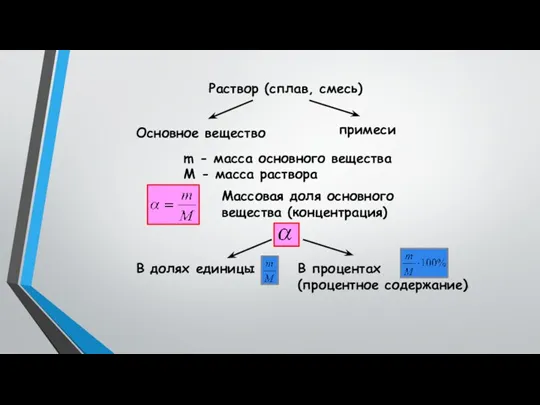
- 2. Раствор (сплав, смесь) Основное вещество примеси m - масса основного вещества M - масса раствора Массовая
- 3. В процессе решения каждой задачи целесообразно действовать по следующей схеме: Изучение условия задачи. Выбор неизвестных величин,
- 4. Решение задач с помощью таблицы.
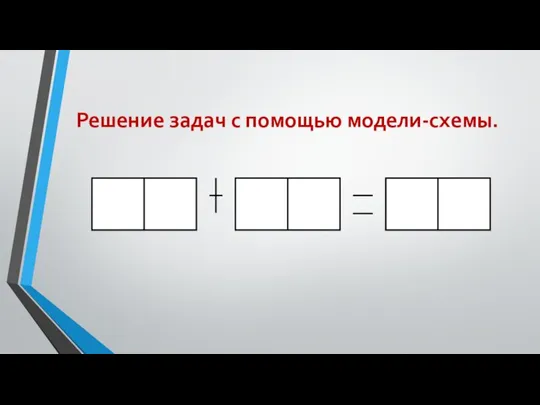
- 5. Решение задач с помощью модели-схемы.
- 6. Метод «рыбки». a, b %- содержание вещества в исходных растворах c % -содержание вещества в искомом
- 7. ЗАДАЧА 1: В емкость, содержащую 12 кг 8%-ного раствора вещества, добавили 4 кг воды. Сколько процентов
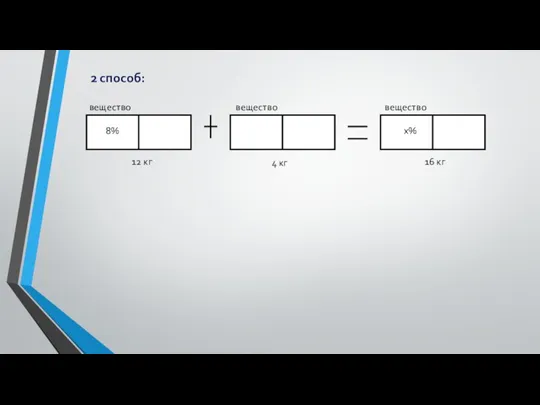
- 8. 2 способ: вещество вещество вещество 8% x% 12 кг 4 кг 16 кг
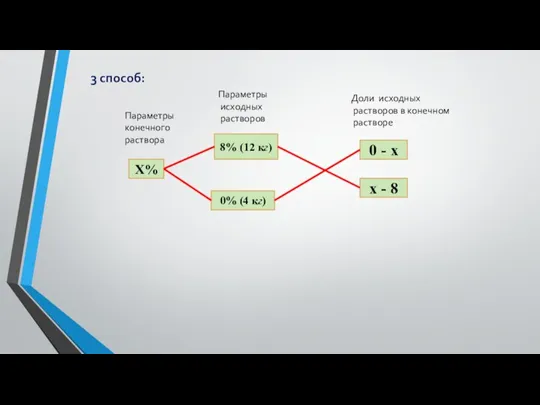
- 9. 3 способ: Параметры конечного раствора Параметры исходных растворов Доли исходных растворов в конечном растворе
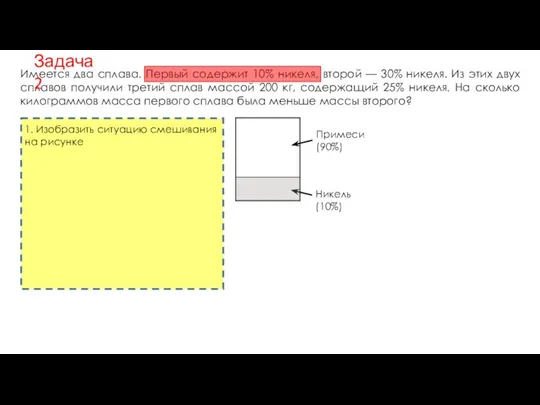
- 10. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили
- 11. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили
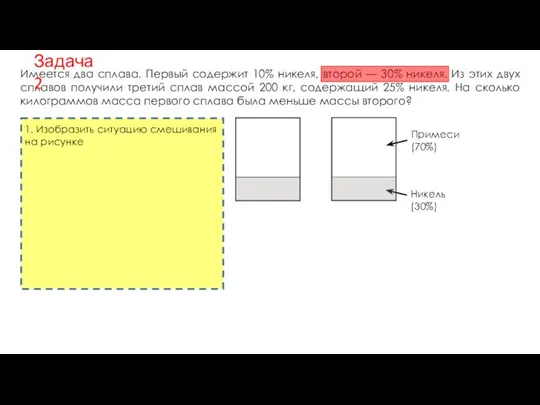
- 12. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили
- 13. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили
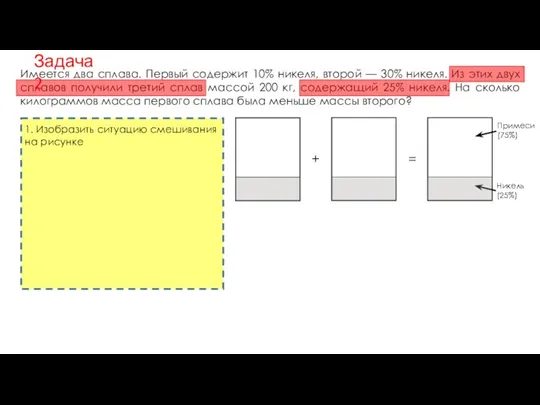
- 14. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили
- 15. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили
- 16. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили
- 17. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили
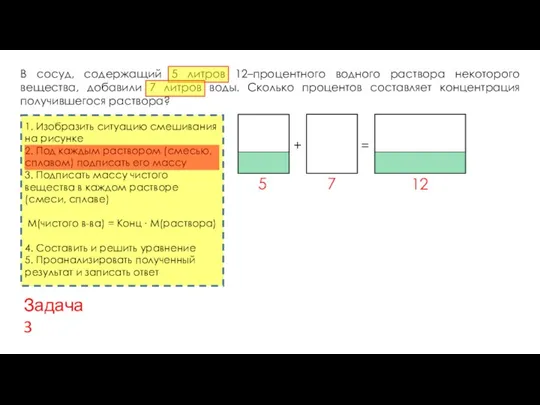
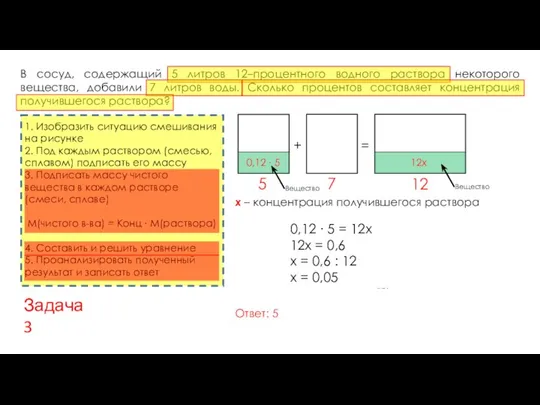
- 18. В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов
- 19. В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов
- 20. В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов
- 22. Скачать презентацию










 Задачи на части
Задачи на части Презентация на тему Круговые диаграммы (5 класс)
Презентация на тему Круговые диаграммы (5 класс)  Угловые измерения. Лекция №6
Угловые измерения. Лекция №6 Решение задач
Решение задач Лабораторные работы по геометрическому материалу
Лабораторные работы по геометрическому материалу Положительные и отрицательные числа. Диагностика
Положительные и отрицательные числа. Диагностика Автоматы и алгоритмы. Комбинационные схемы и конечные автоматы
Автоматы и алгоритмы. Комбинационные схемы и конечные автоматы Математическая логика. Логические выражения
Математическая логика. Логические выражения Вычисление окружности
Вычисление окружности Процент. Знать и уметь находить
Процент. Знать и уметь находить Деятельностный подход при изучении темы Объёмы в 5 и 6 классах
Деятельностный подход при изучении темы Объёмы в 5 и 6 классах Промежуточная аттестация по геометрии
Промежуточная аттестация по геометрии Пифагор Самосский. Теорема Пифагора
Пифагор Самосский. Теорема Пифагора Презентация на тему ГИА 2013. Модуль ГЕОМЕТРИЯ (№13)
Презентация на тему ГИА 2013. Модуль ГЕОМЕТРИЯ (№13)  Решение одной задачи, не лишено здравого смысла
Решение одной задачи, не лишено здравого смысла Прикладная математика. Лекция 1. Геометрический метод решения задачи линейного программирования
Прикладная математика. Лекция 1. Геометрический метод решения задачи линейного программирования Симметрия фигур
Симметрия фигур Геометрические задачи. 10 класс
Геометрические задачи. 10 класс Первый признак равенства треугольников
Первый признак равенства треугольников Неопределенный интеграл
Неопределенный интеграл Сводка и группировка статистических данных
Сводка и группировка статистических данных Вписанная и описанная окружности
Вписанная и описанная окружности Презентация на тему Возникновение измерений в древности
Презентация на тему Возникновение измерений в древности  Нахождение дроби от числа
Нахождение дроби от числа Презентация на тему Решаем задачи (1 класс)
Презентация на тему Решаем задачи (1 класс)  Логарифмы. Свойства логарифмов
Логарифмы. Свойства логарифмов Тренировка интеллекта
Тренировка интеллекта Презентация на тему Число и цифра 3. Состав числа 3 (1 класс)
Презентация на тему Число и цифра 3. Состав числа 3 (1 класс)