Решение задач с использованием теоремы о накрест лежащих углах

Решение задач с использованием
теоремы о накрест лежащих углах

Дано:
m || n
∠3=2∠1
Найти: ∠2, ∠4
Билет № 3
5
6
с

Дано:
m || n
∠3=2∠1
Найти: ∠2, ∠4
Решение:
∠3=∠5 (как вертикальные)
m || n (по условию), с – секущая, значит ∠5=∠4 (н/л углы)
∠1+∠4=1800 (как смежные)
Имеем: ∠4=∠5=∠3=2∠1, тогда
∠1+2∠1=1800
3∠1=1800
∠1=600
∠4=2∠1=1200
∠2=∠1=600 (как соответственные углы при m || n и с – секущей)
Ответ: ∠2=600, ∠4=1200
5
6
с

Билет № 17
Дано:
m || n, с - секущая
∠1 и ∠2 - н/л углы
∠1+∠2=2300
Найти: ∠1, ∠2

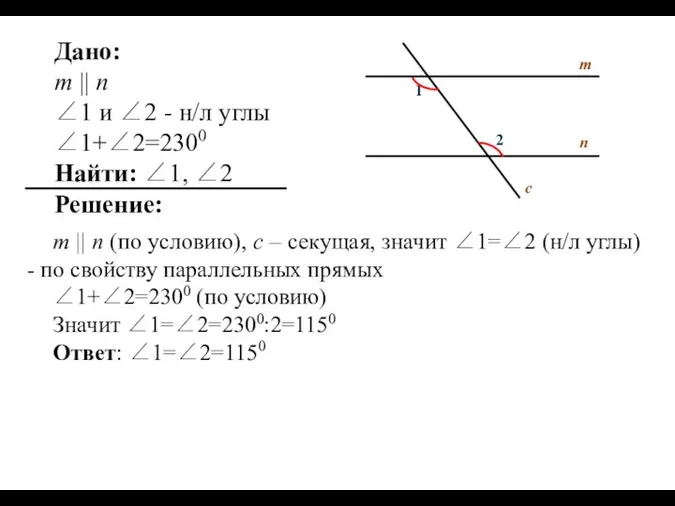
Дано:
m || n
∠1 и ∠2 - н/л углы
∠1+∠2=2300
Найти: ∠1, ∠2
Решение:
m || n (по условию), с – секущая, значит ∠1=∠2 (н/л углы) - по свойству параллельных прямых
∠1+∠2=2300 (по условию)
Значит ∠1=∠2=2300:2=1150
Ответ: ∠1=∠2=1150

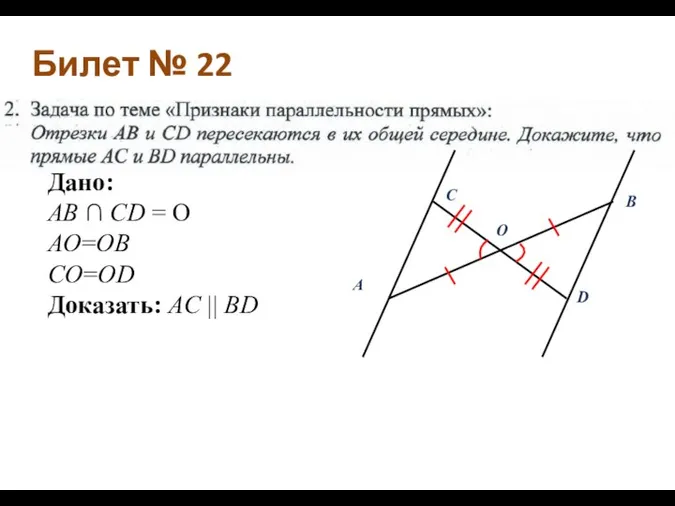
Билет № 22
Дано:
AB ∩ CD = O
AO=OB
CO=OD
Доказать: AC || BD