Предел функции

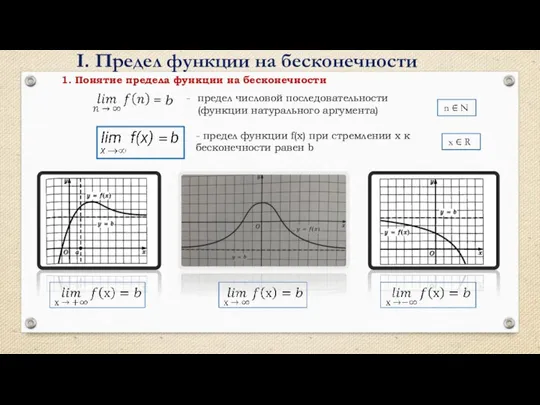
I. Предел функции на бесконечности
- предел функции f(x) при стремлении х к бесконечности равен b
1. Понятие предела функции на бесконечности

I. Предел функции на бесконечности
2. Свойства вычисления пределов функций на бесконечности

Пример 1. Вычислить
Решение.
I. Предел функции на бесконечности

Пример 2. Вычислить
Решение.
II. Предел функции на бесконечности

Пример 3. Вычислить
Решение.
II. Предел функции на бесконечности
6
6

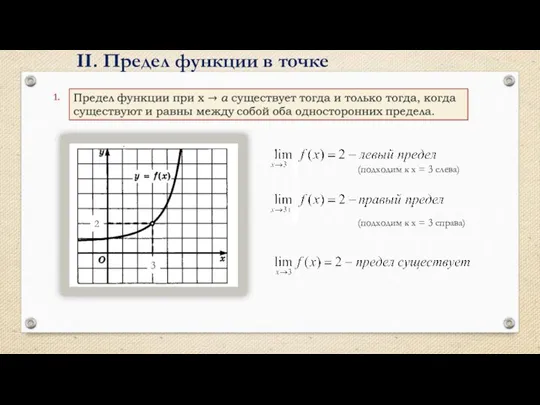
II. Предел функции в точке
(подходим к х = 3 слева)
(подходим к х = 3 справа)
1.

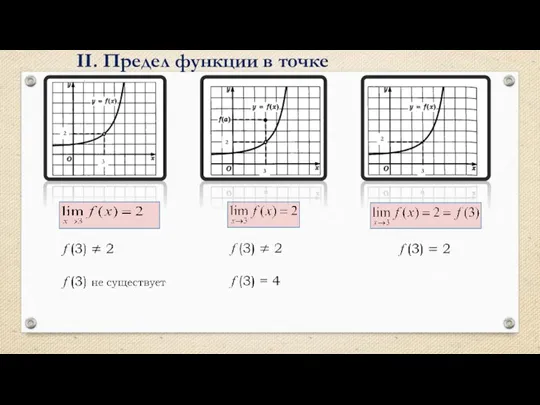
II. Предел функции в точке
3
2
2
2
3
2

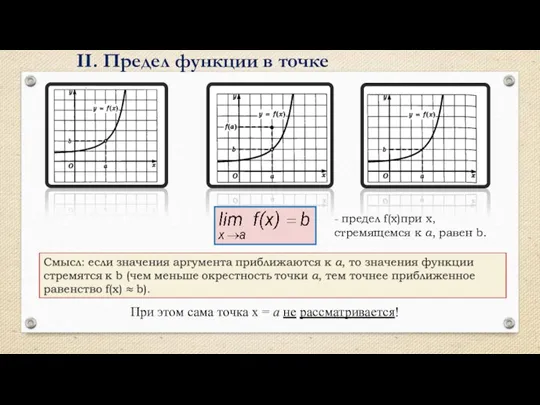
II. Предел функции в точке
При этом сама точка х = а не рассматривается!
- предел f(x)при х, стремящемся к а, равен b.

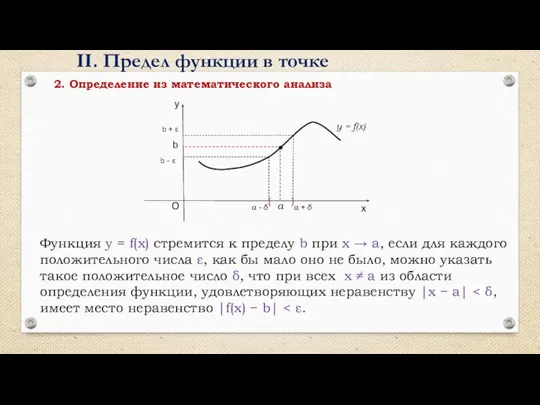
Функция y = f(x) стремится к пределу b при x → a, если для каждого положительного числа ε, как бы мало оно не было, можно указать такое положительное число δ, что при всех x ≠ a из области определения функции, удовлетворяющих неравенству |x − a| < δ, имеет место неравенство |f(x) − b| < ε.
II. Предел функции в точке
2. Определение из математического анализа
у
х
О
а
b
а + δ
а - δ
b + ε
b - ε
y = f(x)

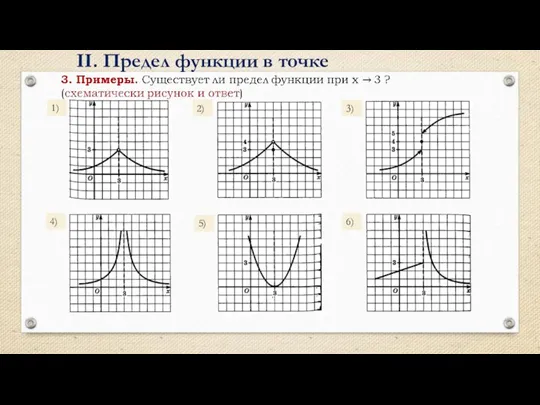
II. Предел функции в точке
1)
2)
3)
4)
5)
6)