07_ ОТС_ Основы теории случайных процессов

Пространство элементарных событий (генеральная совокупность)
Основные понятия теории вероятностей
Все сигналы и все помехи являются случайными, то есть непредсказуемыми.
Математическими моделями случайных сигналов и помех служат случайные процессы.
В основе лежит понятие случайного события
− случайное событие
элементарное событие

Основные понятия теории вероятностей
− случайное событие
− элементарное случайное событие
− вероятностная мера (функция множеств)
− вероятность случайного события
достоверное событие

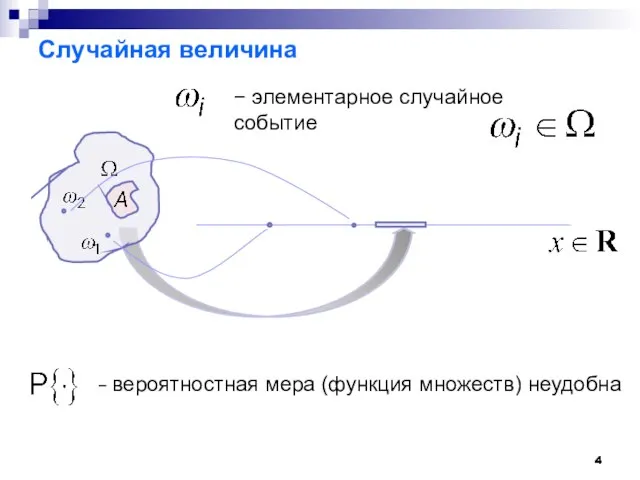
Случайная величина
− элементарное случайное событие
− вероятностная мера (функция множеств) неудобна

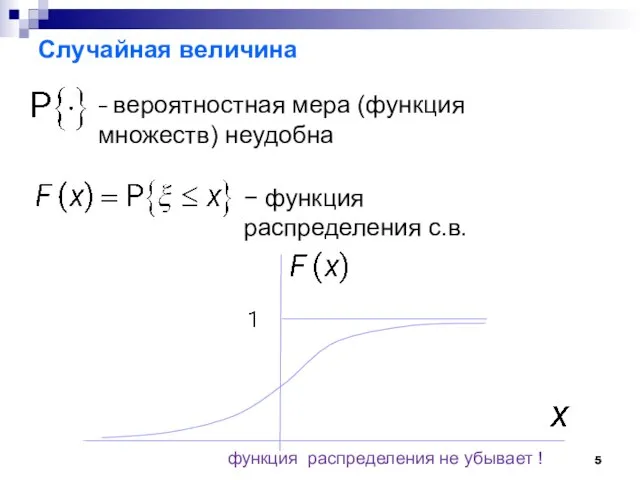
Случайная величина
− вероятностная мера (функция множеств) неудобна
− функция распределения с.в.
функция распределения не убывает !

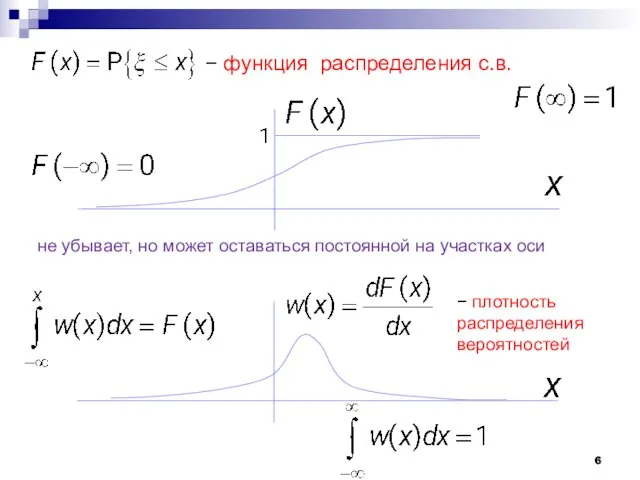
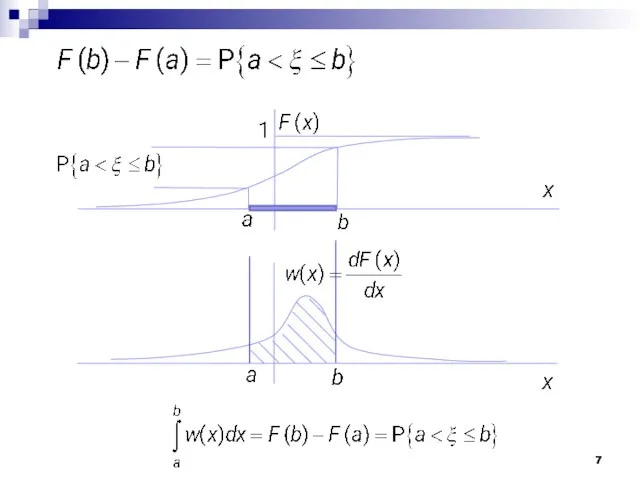
− функция распределения с.в.
не убывает, но может оставаться постоянной на участках оси
− плотность распределения вероятностей

Примеры ФР и ПРВ
равномерное распределение
экспоненциальное распределение

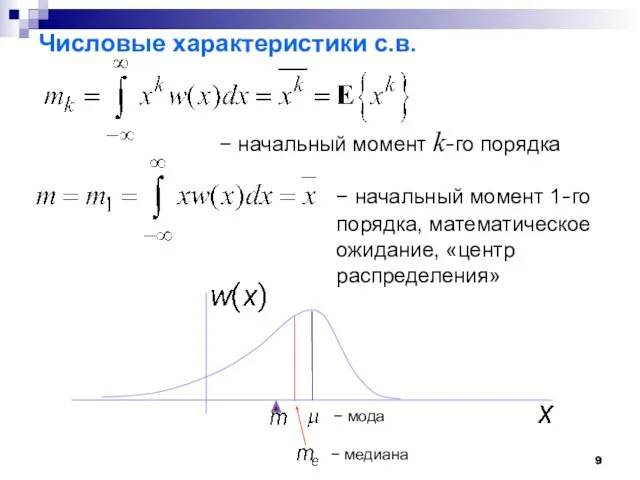
Числовые характеристики с.в.
− начальный момент k-го порядка
− начальный момент 1-го порядка, математическое ожидание, «центр распределения»
− мода
− медиана

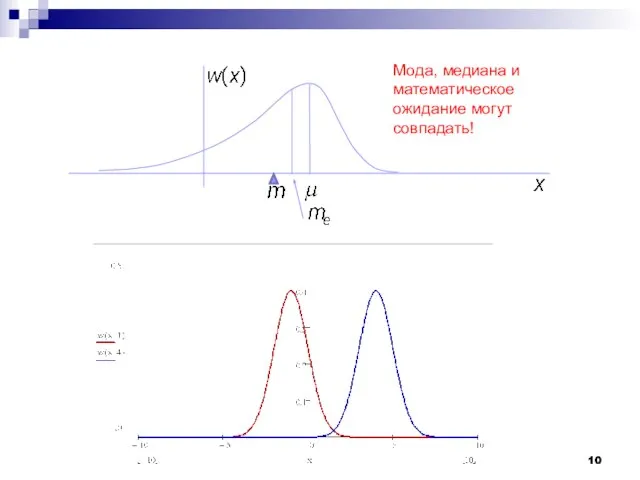
Мода, медиана и математическое ожидание могут совпадать!

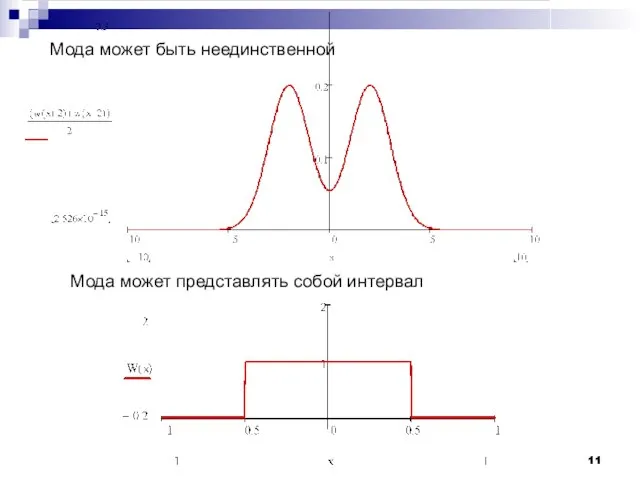
Мода может быть неединственной
Мода может представлять собой интервал

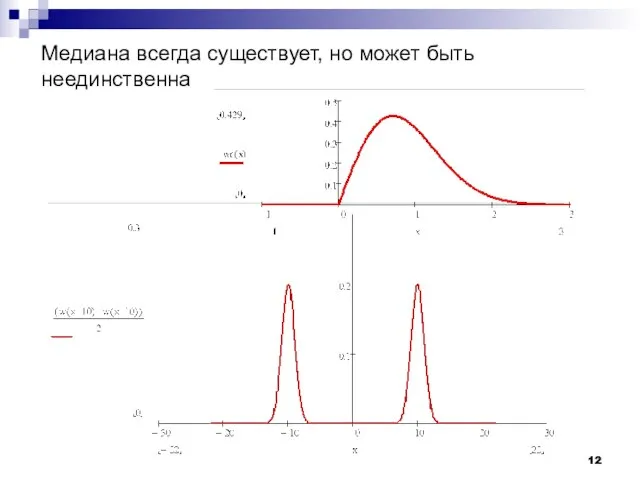
Медиана всегда существует, но может быть неединственна

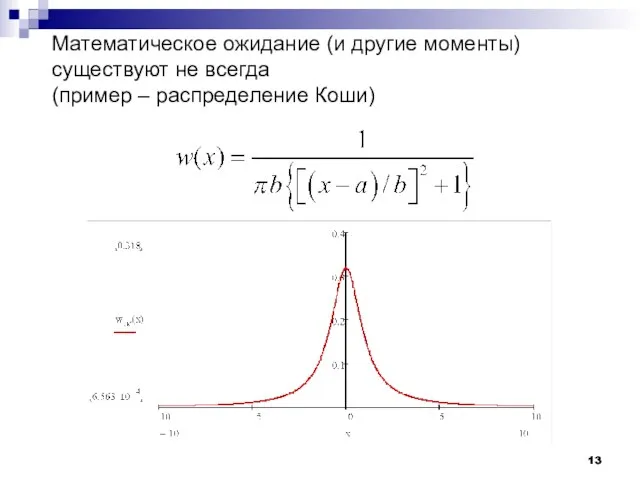
Математическое ожидание (и другие моменты) существуют не всегда
(пример – распределение Коши)

− центральный момент k-го порядка
− центральный момент 2-го порядка (дисперсия)
− среднеквадратическое отклонение (СКО)

− центральный момент 2-го порядка (дисперсия)
− среднеквадратическое отклонение (СКО)
− средний квадрат

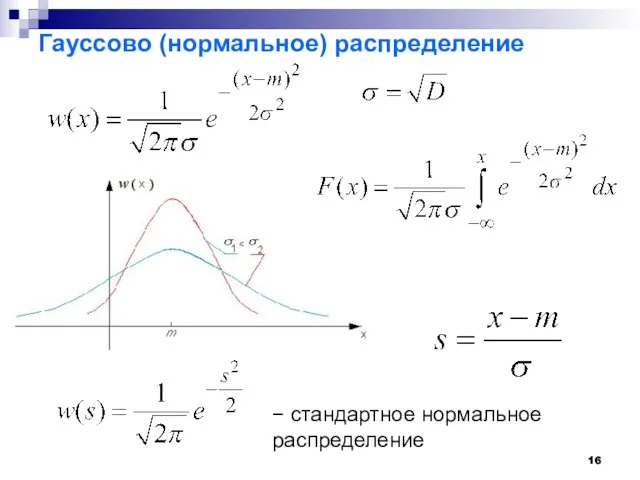
Гауссово (нормальное) распределение
− стандартное нормальное распределение

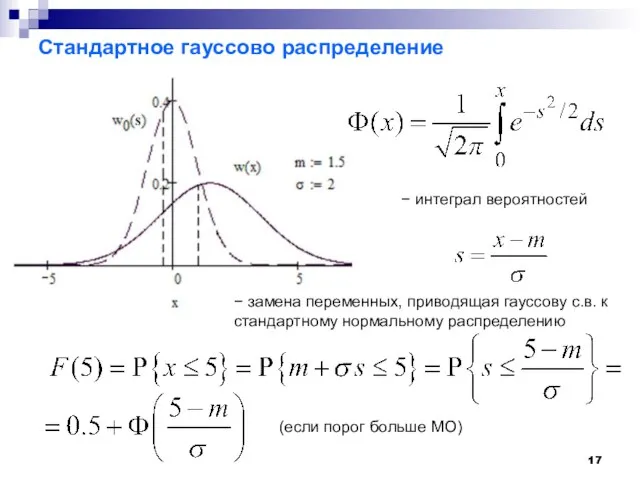
Стандартное гауссово распределение
− интеграл вероятностей
− замена переменных, приводящая гауссову с.в. к стандартному нормальному распределению
(если порог больше МО)

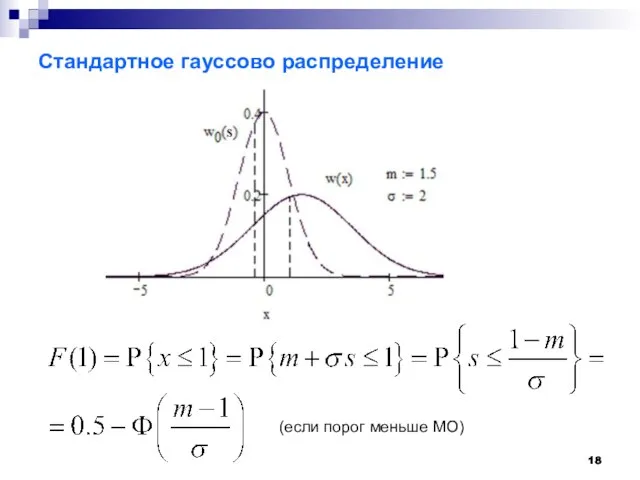
Стандартное гауссово распределение
(если порог меньше МО)

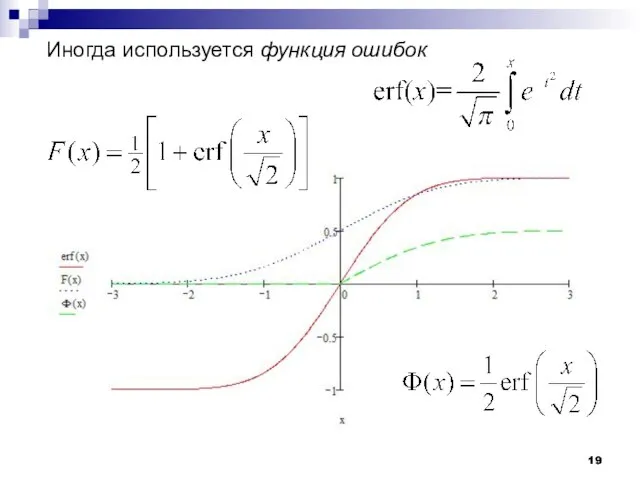
Иногда используется функция ошибок

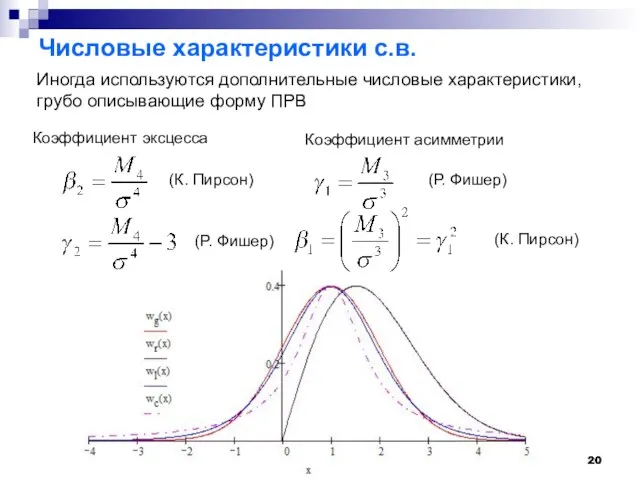
Числовые характеристики с.в.
Иногда используются дополнительные числовые характеристики, грубо описывающие форму ПРВ
Коэффициент эксцесса
Коэффициент асимметрии
(К. Пирсон)
(Р. Фишер)
(Р. Фишер)
(К. Пирсон)

Системы случайных величин
совместная функция распределения
совместная ПРВ

Свойства ФР
не убывает по каждому аргументу
Свойства ПРВ

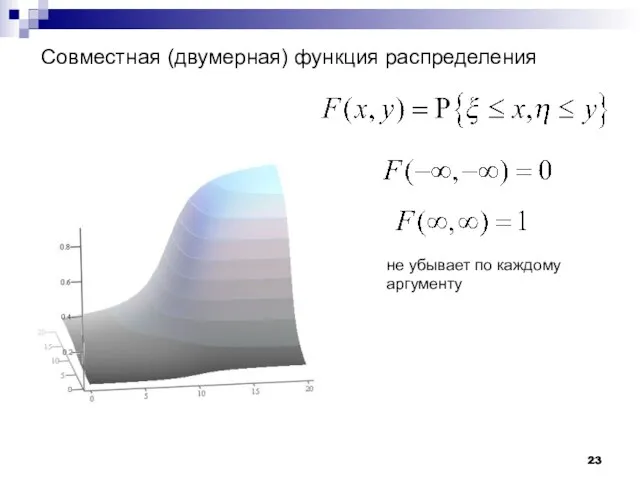
Совместная (двумерная) функция распределения
не убывает по каждому аргументу

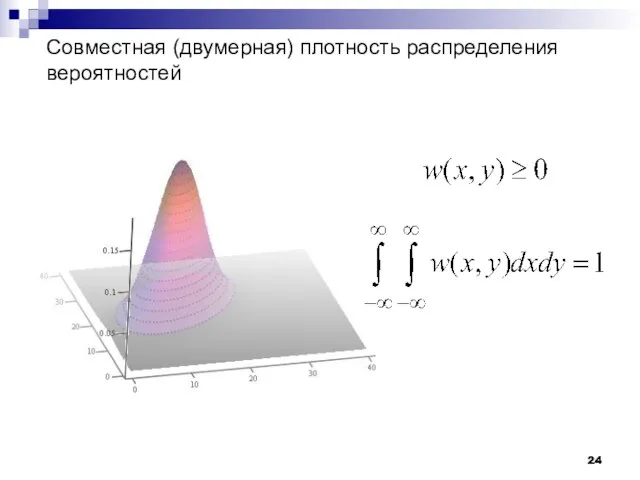
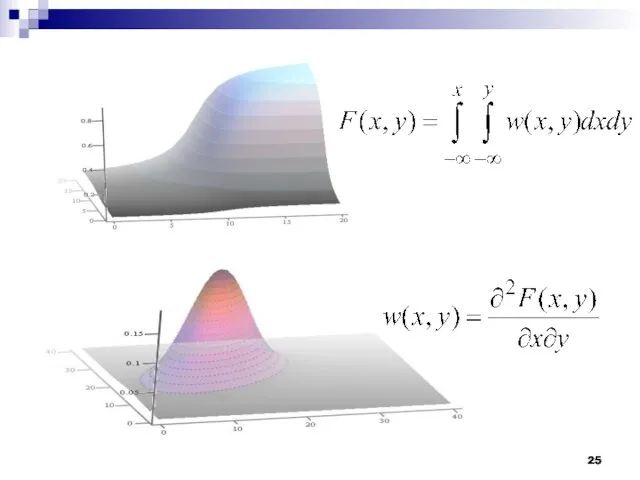
Совместная (двумерная) плотность распределения вероятностей

Числовые характеристики системы 2 случайных величин
Начальные смешанные моменты
Центральные смешанные моменты

ковариационный момент
корреляционный момент

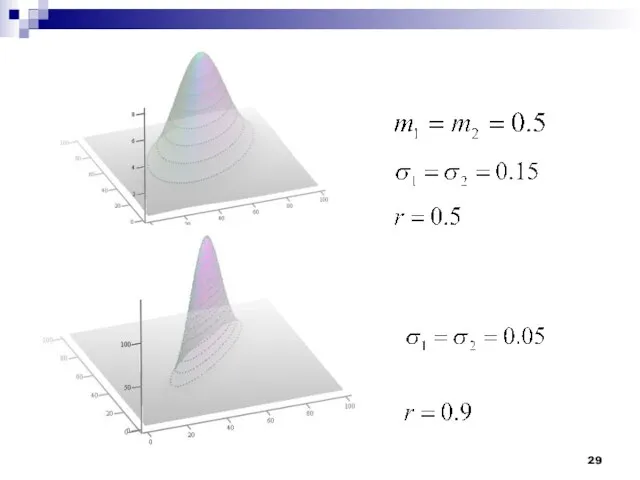
Пример. Пара гауссовских случайных величин
коэффициент корреляции
При нулевом коэффициенте корреляции
Некоррелированные гауссовские с.в. – независимы!