Тригонометрические функции, их свойства и графики

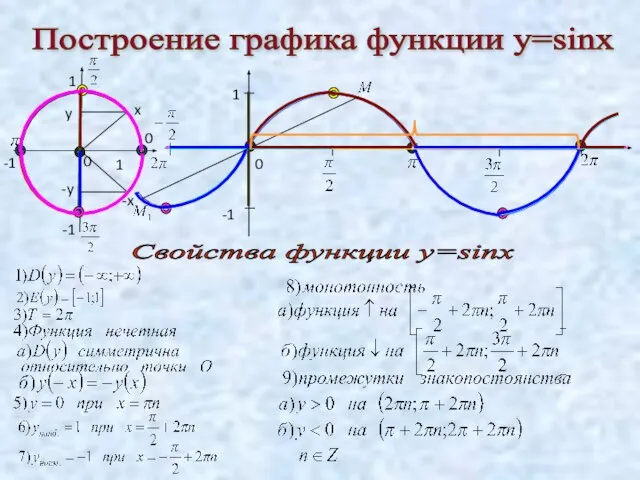
Построение графика функции у=sinx
1
-1
0
0
0
Свойства функции у=sinx
x
-x
y
-y
1
-1
-1
1

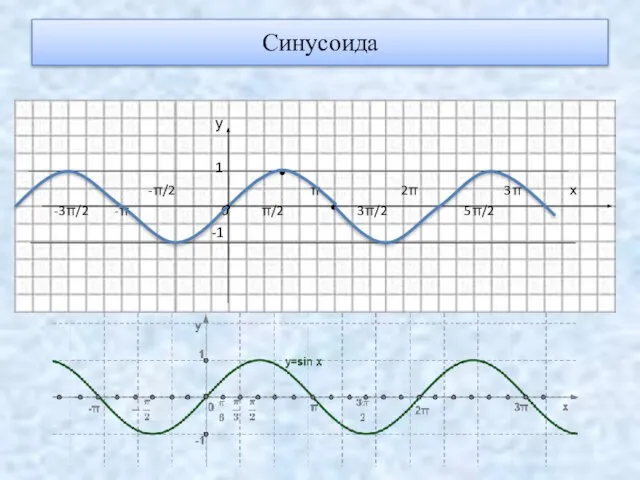
Синусоида
у
1
-π/2 π 2π 3π х
-3π/2 -π 0 π/2 3π/2 5π/2
-1

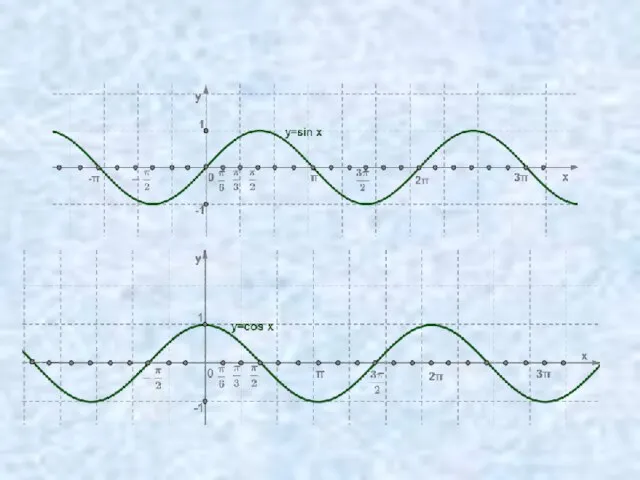
Построение графика функции у=cosx
1
-1
0
0
0
Свойства функции у=cosx
x
-x
1
-1
-1
1
y

Преобразование графиков функций y=sin x и y=cos x
Параллельный перенос вдоль оси Параллельный перенос вдоль оси OY
Параллельный перенос вдоль оси Параллельный перенос вдоль оси OX
Растяжение (сжатие) в Растяжение (сжатие) в k Растяжение (сжатие) в k раз вдоль оси Растяжение (сжатие) в k раз вдоль оси OY
Растяжение (сжатие) в Растяжение (сжатие) в k Растяжение (сжатие) в k раз вдоль оси Растяжение (сжатие) в k раз вдоль оси OX
Симметрия относительно оси абсцисс
Пример построения графика сложной функции

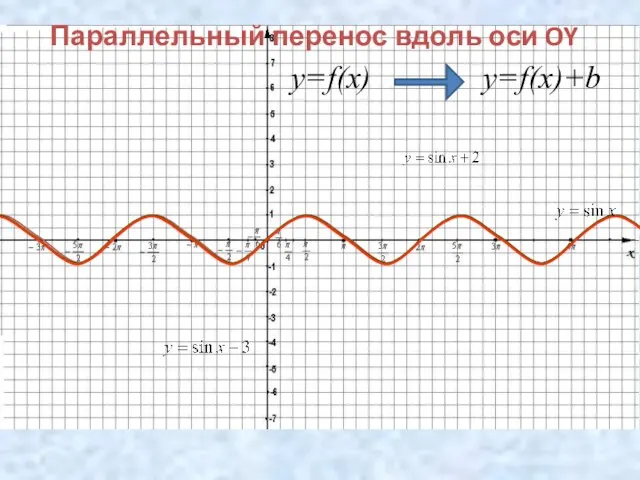
Параллельный перенос вдоль оси OY
y=f(x) y=f(x)+b

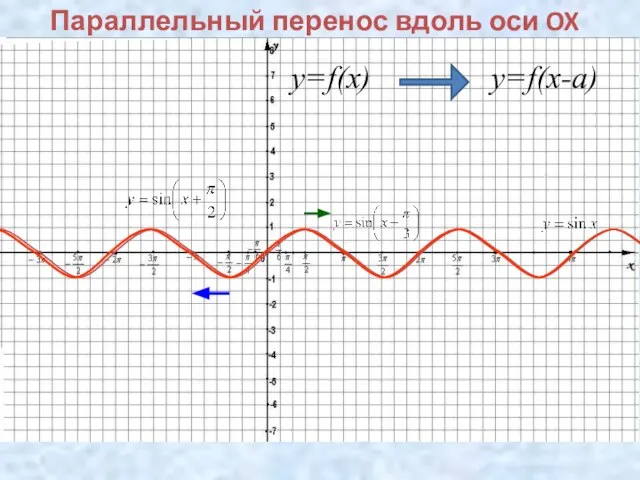
Параллельный перенос вдоль оси OX
y=f(x) y=f(x-a)

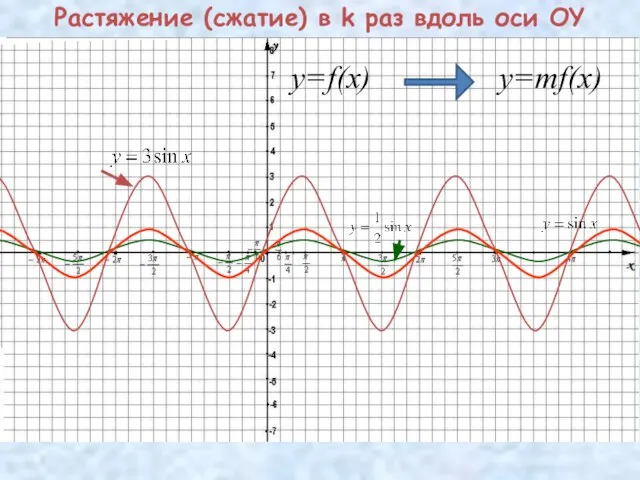
Растяжение (сжатие) в k раз вдоль оси OY
y=f(x) y=mf(x)

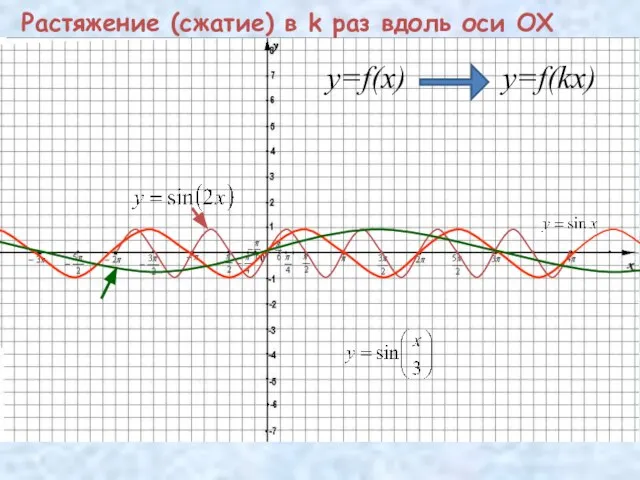
Растяжение (сжатие) в k раз вдоль оси OX
y=f(x) y=f(kx)

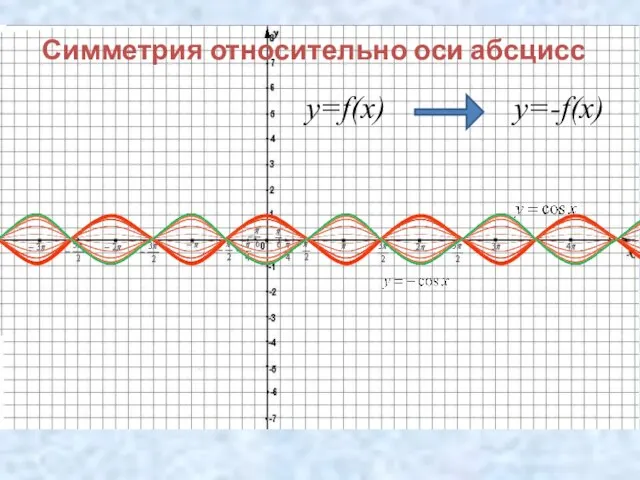
Симметрия относительно оси абсцисс
y=f(x) y=-f(x)

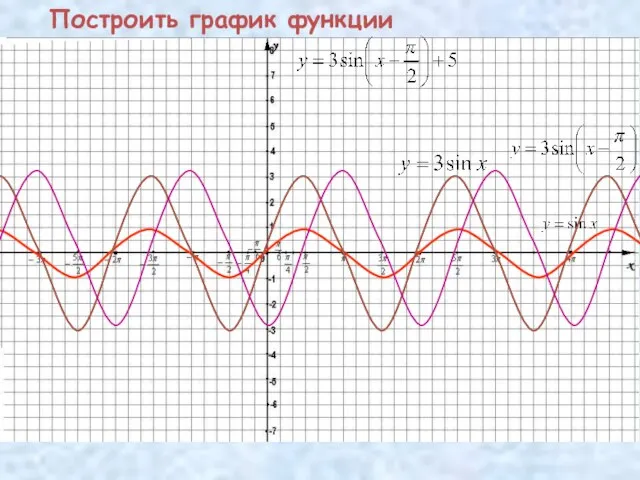
Построить график функции

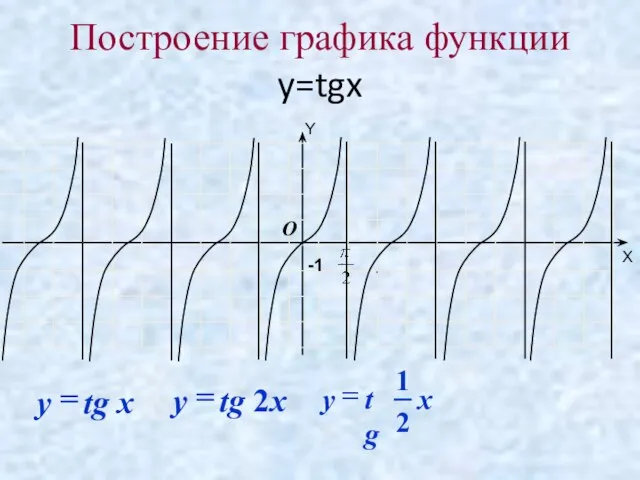
Построение графика функции y=tgx
-1
O
Y
X

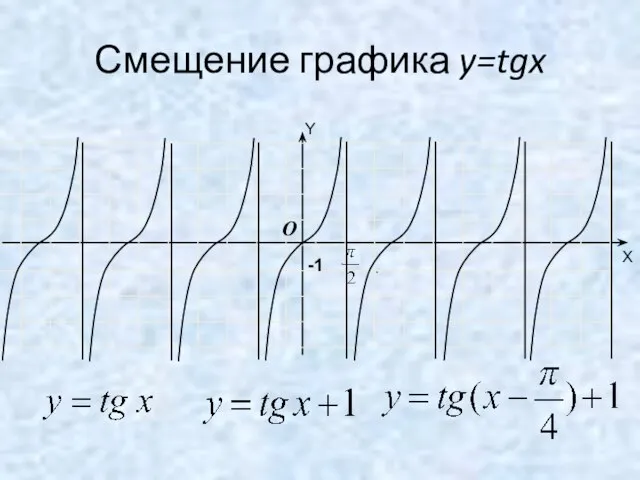
Смещение графика y=tgx
-1
O
Y
X

Свойства графика функции y=tg x
Область определения: x≠π/2+πn, n∈Z
Множество значений: y∈(-∞;∞)
Функция периодическая Т=π
Функция нечетная
y=0, при x=πn, n∈Z
y>0, при x∈(πn; π/2+πn), n∈Z
y<0, при x∈(-π/2+πn; πn), n∈Z
Функция возрастает на интервалах: (-π/2+πn; π/2+πn), n∈Z

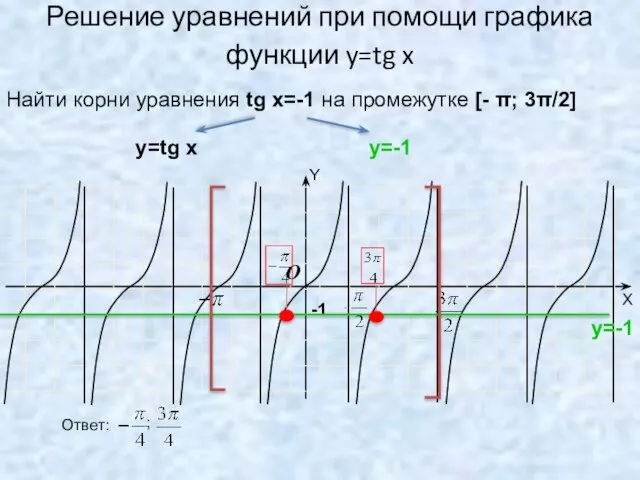
Решение уравнений при помощи графика функции y=tg x
-1
O
Найти корни уравнения tg x=-1 на промежутке [- π; 3π/2]
y=tg x
y=-1
Ответ:
;
Y
X
y=-1

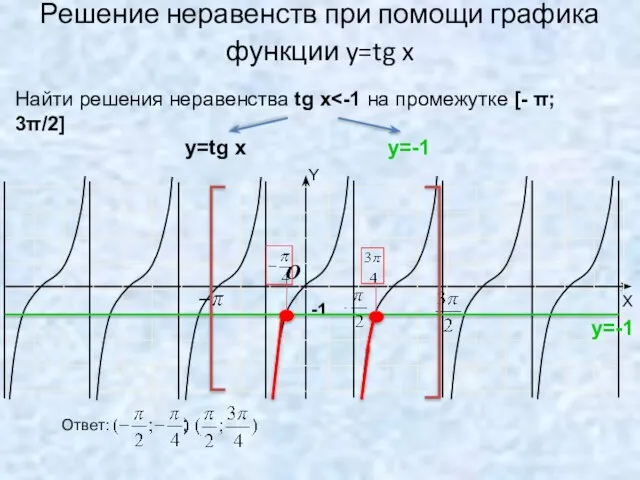
Решение неравенств при помощи графика функции y=tg x
-1
O
Найти решения неравенства tg x<-1 на промежутке [- π; 3π/2]
y=tg x
y=-1
Ответ:
;
Y
X
y=-1

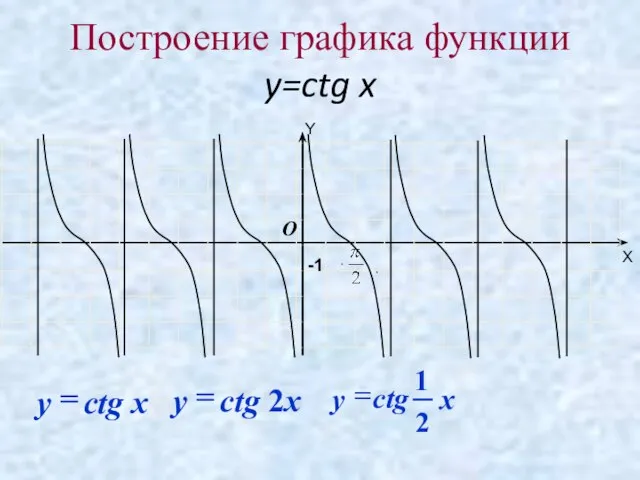
Построение графика функции y=ctg x
-1
O
Y
X

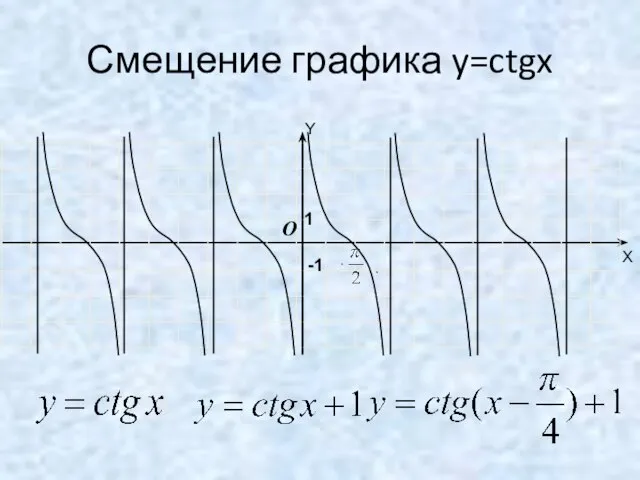
Смещение графика y=ctgx
-1
O
1
Y
X

Свойства графика функции y=ctg x
Область определения: x≠πn, n∈Z
Множество значений: y∈(-∞;∞)
Функция периодическая T=π
Функция нечетная
y=0, при x=π/2+πn, n∈Z
y>0, при x∈(0+πn; π/2+πn), n∈Z
y<0, при x∈(-π/2+πn; 0+πn), n∈Z
Функция убывает на интервалах (πn; π+πn), n∈Z

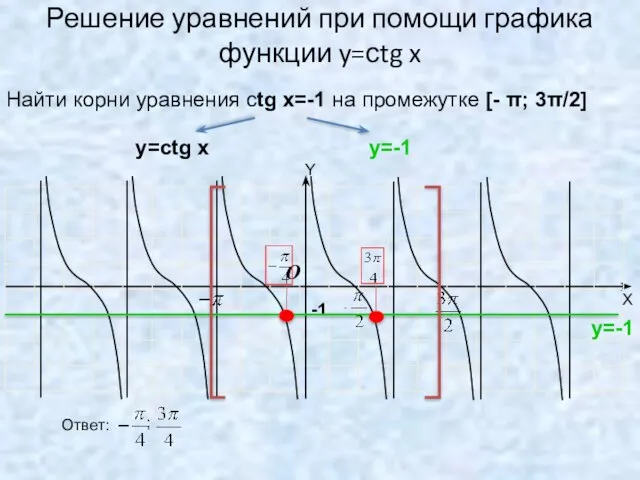
Решение уравнений при помощи графика функции y=сtg x
-1
O
Найти корни уравнения сtg x=-1 на промежутке [- π; 3π/2]
y=сtg x
y=-1
Ответ:
;
Y
X
y=-1

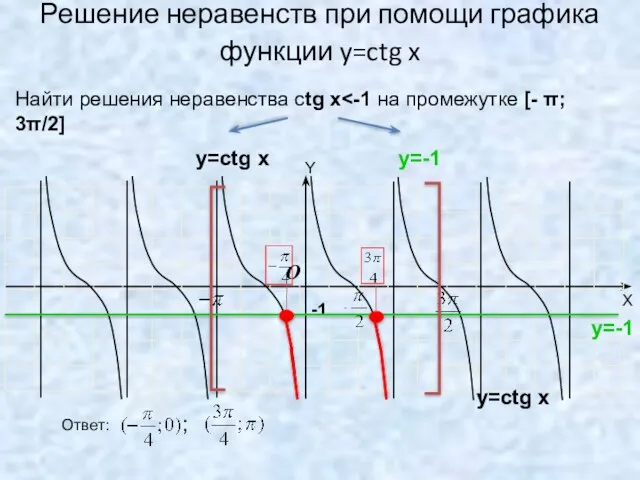
Решение неравенств при помощи графика функции y=ctg x
-1
O
Найти решения неравенства ctg x<-1 на промежутке [- π; 3π/2]
y=сtg x
y=-1
Ответ:
;
Y
X
y=-1
y=сtg x