Окружность.Круг

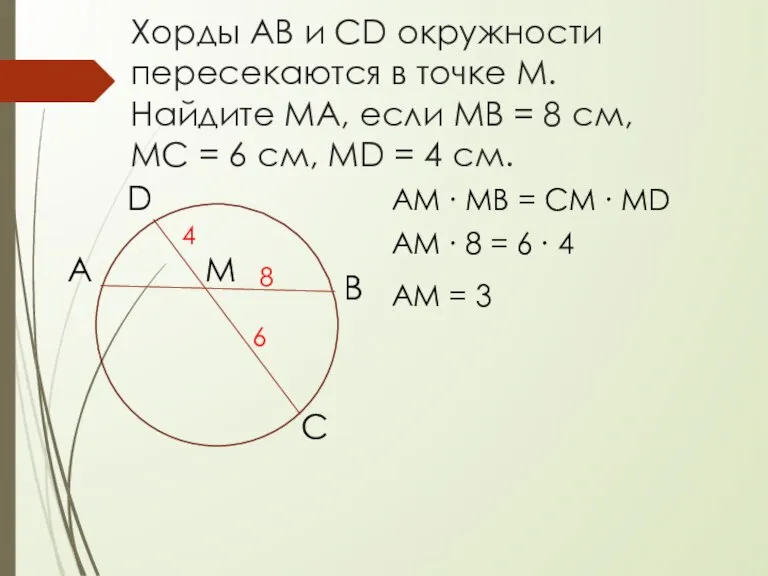
Хорды АВ и CD окружности пересекаются в точке М. Найдите МА, если МВ = 8 см, МС = 6 см, МD = 4 см.
А
В
С
D
M
AМ ∙ МВ = СМ ∙ MD
8
4
6
AМ ∙ 8 = 6 ∙ 4
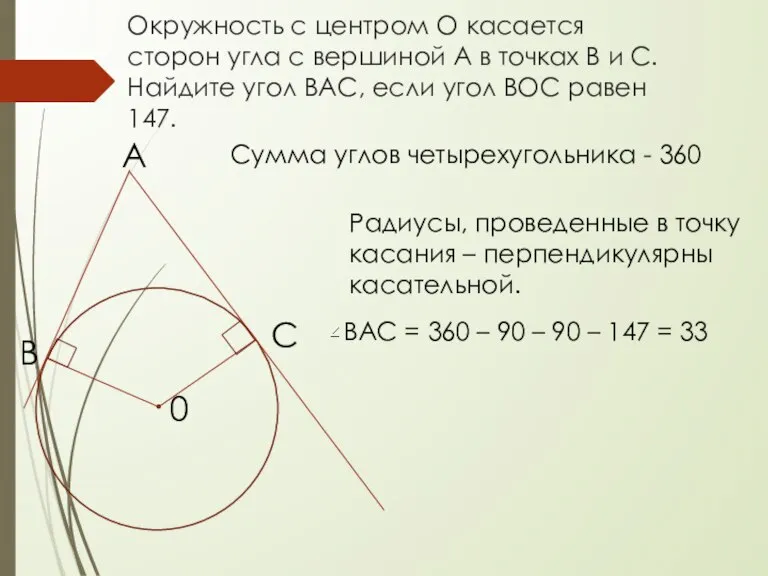
AМ = 3

Окружность с центром О касается сторон угла с вершиной А в точках В и С. Найдите угол ВАС, если угол ВОС равен 147.
А
С
В
0
Сумма углов четырехугольника - 360
Радиусы, проведенные в точку касания – перпендикулярны касательной.
ВАС = 360 – 90 – 90 – 147 = 33

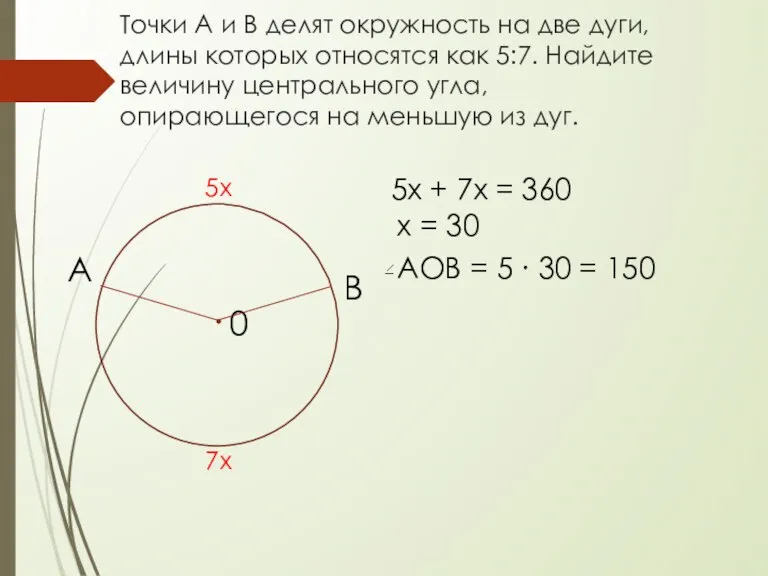
Точки А и В делят окружность на две дуги, длины которых относятся как 5:7. Найдите величину центрального угла, опирающегося на меньшую из дуг.
А
В
5х
7х
0
5х + 7х = 360
х = 30
АОВ = 5 ∙ 30 = 150

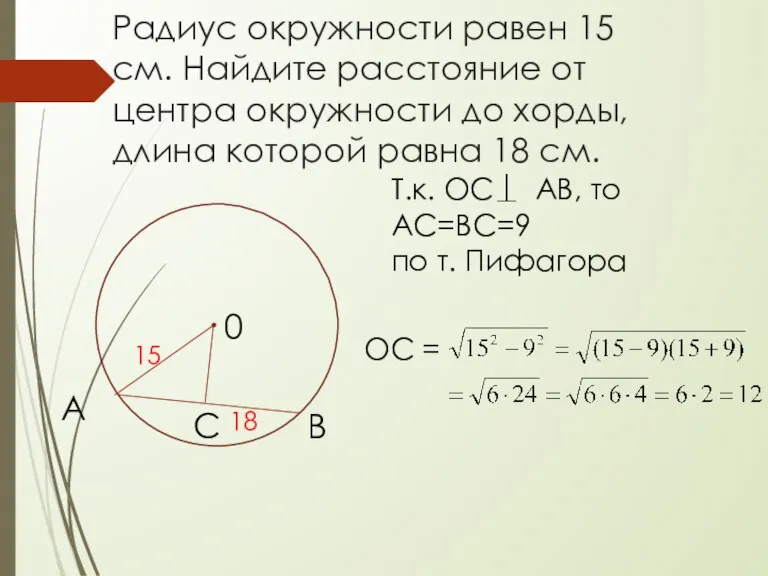
Радиус окружности равен 15 см. Найдите расстояние от центра окружности до хорды, длина которой равна 18 см.
А
В
С
18
15
0
Т.к. ОС АВ, то АС=ВС=9
по т. Пифагора
ОС =

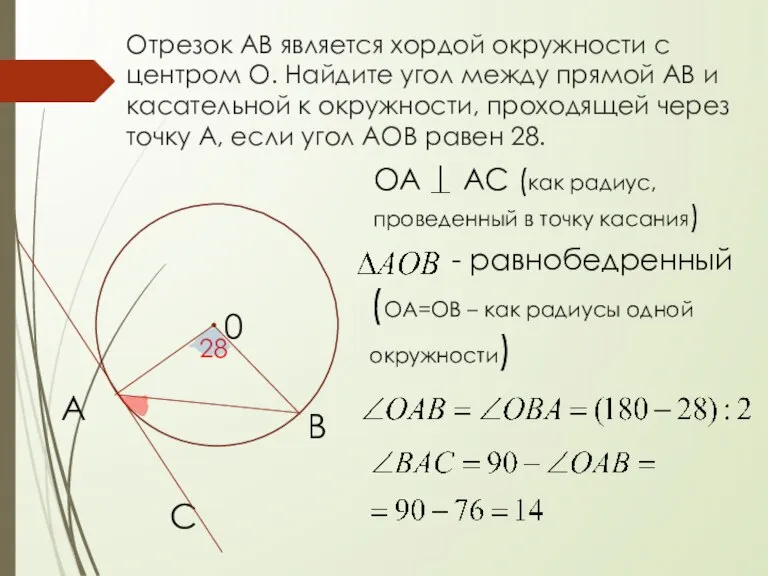
Отрезок АВ является хордой окружности с центром О. Найдите угол между прямой АВ и касательной к окружности, проходящей через точку А, если угол АОВ равен 28.
А
В
С
28
0
ОА АС (как радиус, проведенный в точку касания)
- равнобедренный
(ОА=ОВ – как радиусы одной окружности)

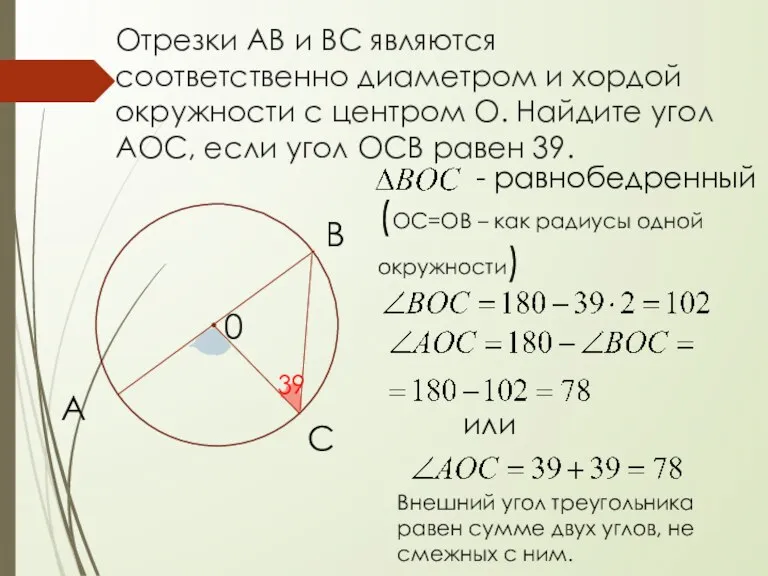
Отрезки АВ и ВС являются соответственно диаметром и хордой окружности с центром О. Найдите угол АОС, если угол ОСВ равен 39.
А
В
39
0
С
- равнобедренный
(ОС=ОВ – как радиусы одной окружности)
или
Внешний угол треугольника равен сумме двух углов, не смежных с ним.

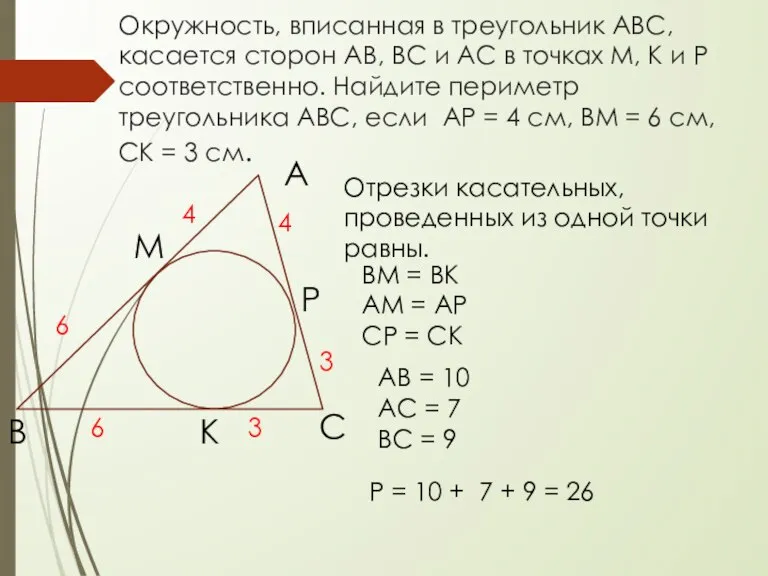
Окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС в точках М, К и Р соответственно. Найдите периметр треугольника АВС, если АР = 4 см, ВМ = 6 см, СК = 3 см.
А
В
С
М
К
Р
4
3
6
Отрезки касательных, проведенных из одной точки равны.
ВМ = ВК
АМ = АР
СР = СК
6
3
4
АВ = 10
АС = 7
ВС = 9
Р = 10 + 7 + 9 = 26

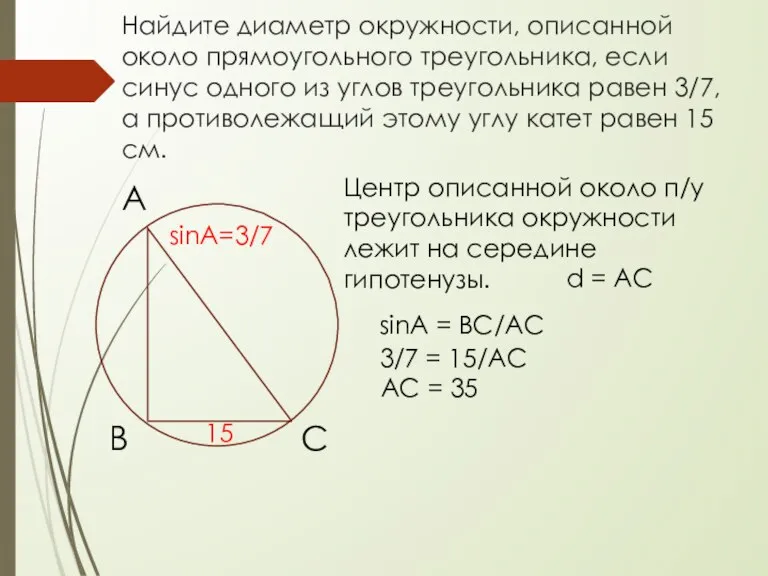
Найдите диаметр окружности, описанной около прямоугольного треугольника, если синус одного из углов треугольника равен 3/7, а противолежащий этому углу катет равен 15 см.
А
В
С
Центр описанной около п/у треугольника окружности лежит на середине гипотенузы.
d = AC
sinA=3/7
15
sinA = ВС/АС
3/7 = 15/АС
АС = 35

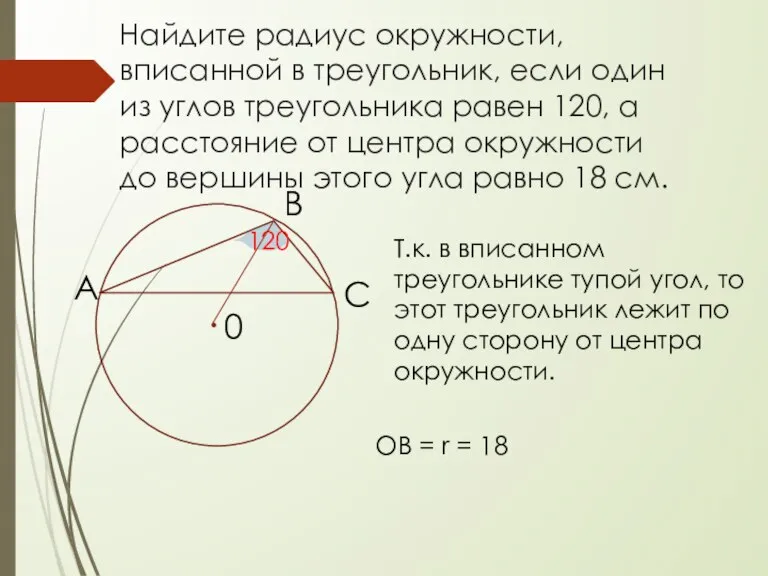
Найдите радиус окружности, вписанной в треугольник, если один из углов треугольника равен 120, а расстояние от центра окружности до вершины этого угла равно 18 см.
0
Т.к. в вписанном треугольнике тупой угол, то этот треугольник лежит по одну сторону от центра окружности.
А
В
С
120
ОВ = r = 18

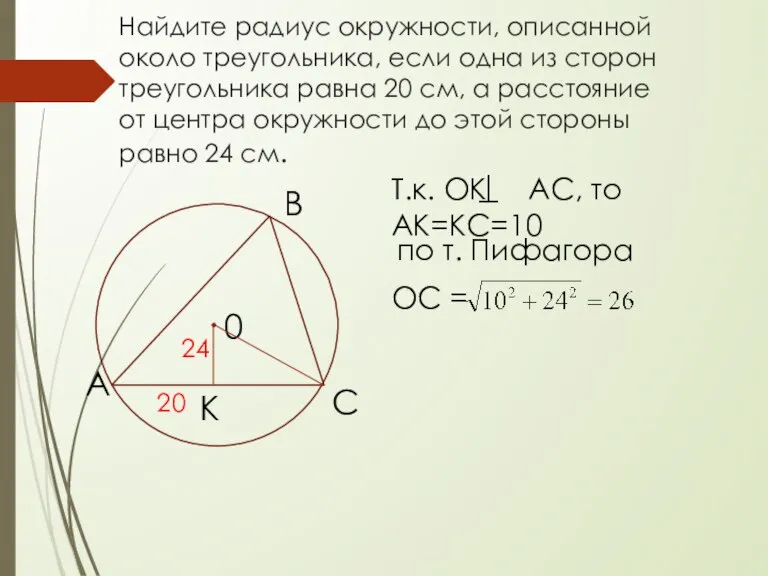
Найдите радиус окружности, описанной около треугольника, если одна из сторон треугольника равна 20 см, а расстояние от центра окружности до этой стороны равно 24 см.
0
А
В
20
С
24
Т.к. ОК АС, то АК=КС=10
К
по т. Пифагора
ОС =

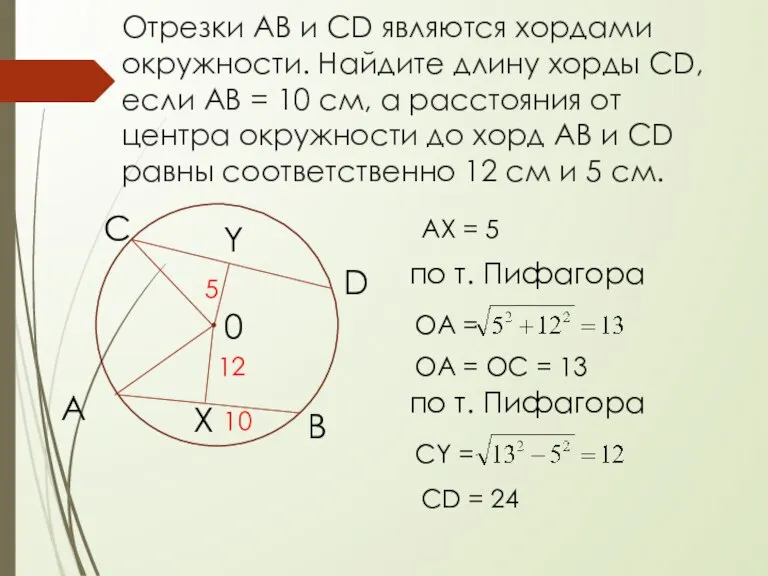
Отрезки АВ и CD являются хордами окружности. Найдите длину хорды CD, если АВ = 10 см, а расстояния от центра окружности до хорд АВ и CD равны соответственно 12 см и 5 см.
А
В
X
12
5
0
C
D
10
Y
АХ = 5
по т. Пифагора
ОА =
ОА = ОС = 13
по т. Пифагора
СY =
CD = 24

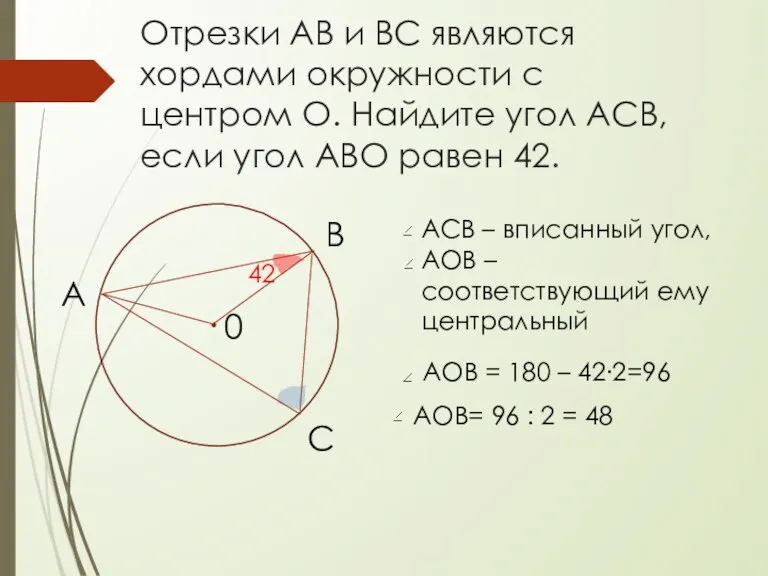
Отрезки АВ и BC являются хордами окружности с центром О. Найдите угол АСВ, если угол АВО равен 42.
А
В
42
0
С
АСВ – вписанный угол,
АОВ – соответствующий ему центральный
АОВ = 180 – 42∙2=96
АОВ= 96 : 2 = 48

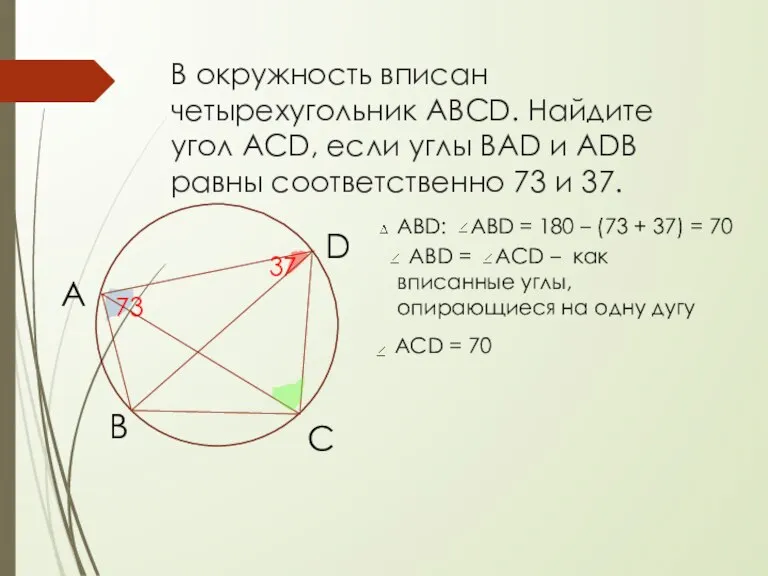
В окружность вписан четырехугольник АВСD. Найдите угол АСD, если углы BAD и ADB равны соответственно 73 и 37.
А
В
37
С
D
73
ABD: ABD = 180 – (73 + 37) = 70
АВD = ACD – как вписанные углы, опирающиеся на одну дугу
AСD = 70

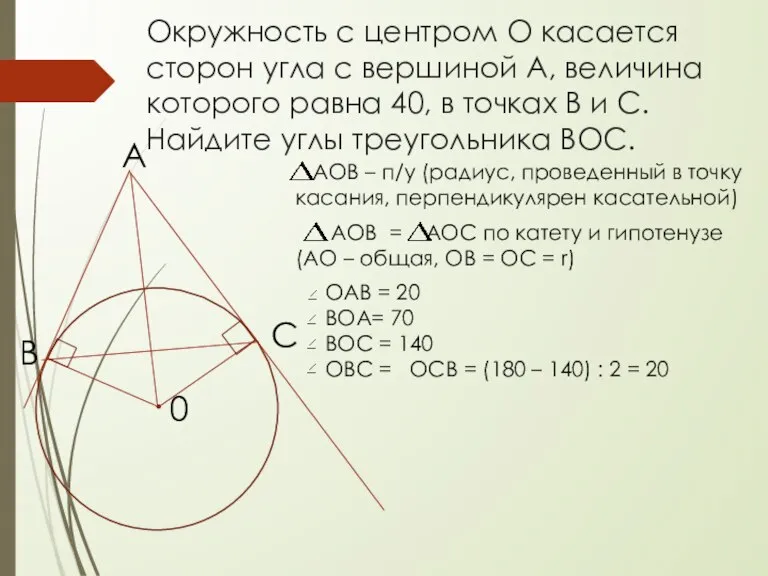
Окружность с центром О касается сторон угла с вершиной А, величина которого равна 40, в точках В и С. Найдите углы треугольника ВОС.
А
С
В
0
АОВ – п/у (радиус, проведенный в точку касания, перпендикулярен касательной)
АОВ = АОС по катету и гипотенузе (АО – общая, ОВ = ОС = r)
ОАВ = 20
ВОА= 70
ВОС = 140
ОВС = ОСВ = (180 – 140) : 2 = 20

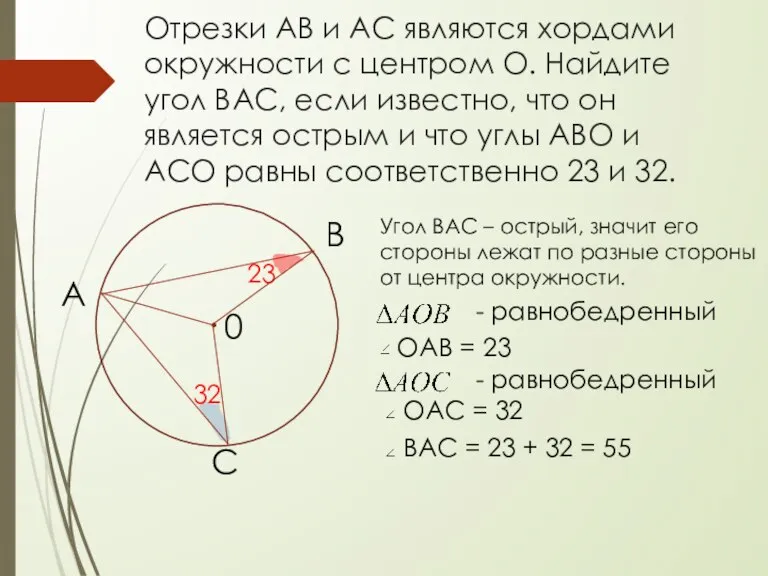
Отрезки АВ и АС являются хордами окружности с центром О. Найдите угол ВАС, если известно, что он является острым и что углы АВО и АСО равны соответственно 23 и 32.
А
В
23
0
С
32
Угол ВАС – острый, значит его стороны лежат по разные стороны от центра окружности.
- равнобедренный
- равнобедренный
ОАВ = 23
ОАС = 32
ВАС = 23 + 32 = 55

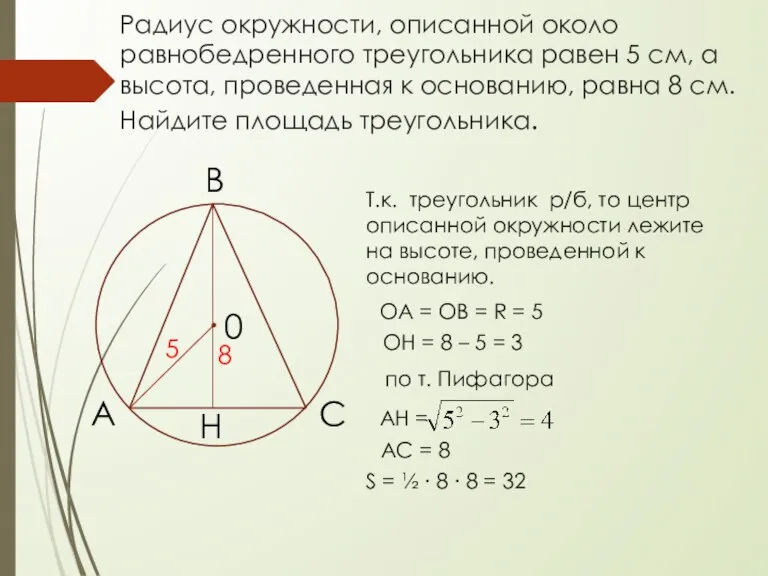
Радиус окружности, описанной около равнобедренного треугольника равен 5 см, а высота, проведенная к основанию, равна 8 см. Найдите площадь треугольника.
0
А
В
С
5
8
Н
Т.к. треугольник р/б, то центр описанной окружности лежите на высоте, проведенной к основанию.
ОА = ОВ = R = 5
ОН = 8 – 5 = 3
по т. Пифагора
АН =
АС = 8
S = ½ ∙ 8 ∙ 8 = 32

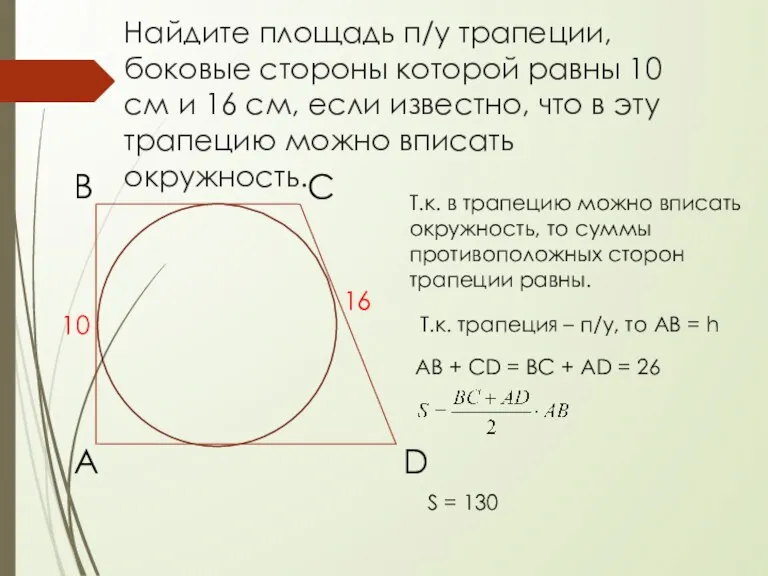
Найдите площадь п/у трапеции, боковые стороны которой равны 10 см и 16 см, если известно, что в эту трапецию можно вписать окружность.
10
16
Т.к. в трапецию можно вписать окружность, то суммы противоположных сторон трапеции равны.
А
В
С
D
АВ + CD = ВС + AD = 26
Т.к. трапеция – п/у, то АВ = h
S = 130

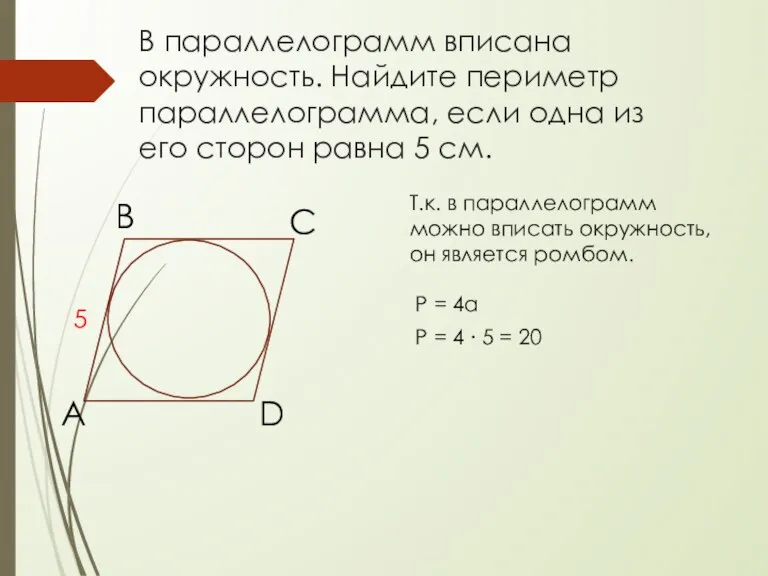
В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 5 см.
5
А
В
D
С
Т.к. в параллелограмм можно вписать окружность, он является ромбом.
Р = 4а
Р = 4 ∙ 5 = 20