- Главная
- Математика
- Базис линейнай прасторы. Каардынаты

Содержание
Слайд 3Тэарэма 1. Маюць месца наступныя сцведжанні для кожнай n – мернай лінейнай
Тэарэма 1. Маюць месца наступныя сцведжанні для кожнай n – мернай лінейнай

прасторы :
1) адвольная сістэма вектараў, у якой іх колькасць большая за n, лінейна залежная;
2) адвольная сістэма з n лінейна незалежных вектараў задае базіс;
3) адвольную лінейна незалежную сістэму вектараў, колькасць вектараў у якой меньшая за n, можна дапоўніць да базісу.
Доказ. 1). Першае сцверджанне вынікае з Тэарэмы аб лінейнай незалежнасці сістэмы вектараў мінулага параграфа.
2). Хай сістэма вектараў a1, a2 ,.., an (1) л.н.з. сістэма вектараў n – мернай лінейнай прасторы, а b – адвольны вектар прасторы. Згодна 1) сістэма вектараў a1, a2 ,.., an, b (2) л.з. Згодна выніку з Тэарэмы аб лінейнай незалежнасці сістэмы вектараў вектар b лінейна выражаецца праз сістэму (1). Значыць, (1) – базіс V.
1) адвольная сістэма вектараў, у якой іх колькасць большая за n, лінейна залежная;
2) адвольная сістэма з n лінейна незалежных вектараў задае базіс;
3) адвольную лінейна незалежную сістэму вектараў, колькасць вектараў у якой меньшая за n, можна дапоўніць да базісу.
Доказ. 1). Першае сцверджанне вынікае з Тэарэмы аб лінейнай незалежнасці сістэмы вектараў мінулага параграфа.
2). Хай сістэма вектараў a1, a2 ,.., an (1) л.н.з. сістэма вектараў n – мернай лінейнай прасторы, а b – адвольны вектар прасторы. Згодна 1) сістэма вектараў a1, a2 ,.., an, b (2) л.з. Згодна выніку з Тэарэмы аб лінейнай незалежнасці сістэмы вектараў вектар b лінейна выражаецца праз сістэму (1). Значыць, (1) – базіс V.
Слайд 5Каардынаты
Каардынаты

- Предыдущая
Изменения в ТК РФСледующая -
Расчет по химическим уравнениям


 Центральная симметрия
Центральная симметрия Логарифмические уравнения
Логарифмические уравнения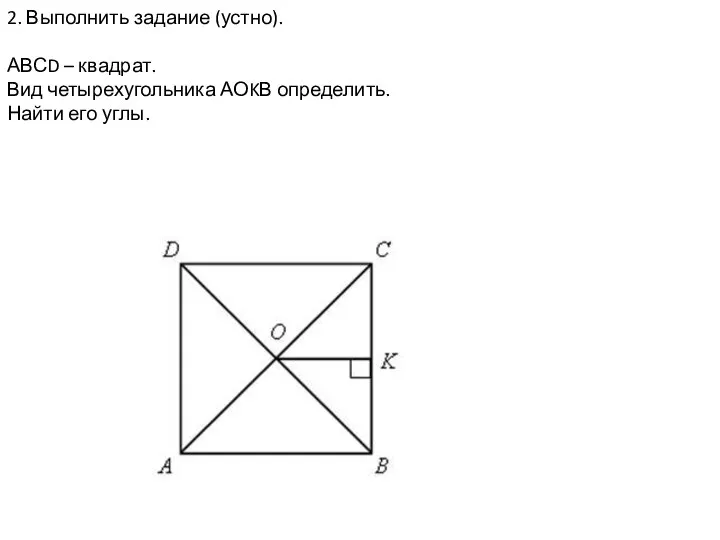 Параллелограмм и трапеция. Урок 7
Параллелограмм и трапеция. Урок 7 Признак существования определенного интеграла. Лекция №7
Признак существования определенного интеграла. Лекция №7 Дифференциальные уравнения I порядка с разделяющимися переменными
Дифференциальные уравнения I порядка с разделяющимися переменными Геометрический конструктор GeoGebra
Геометрический конструктор GeoGebra Степень с рациональным показателем. Преобразование выражений, содержащих степень с рациональным показателем
Степень с рациональным показателем. Преобразование выражений, содержащих степень с рациональным показателем Откуда к нам пришли отрицательные числа? Сказка бабушки Тортилы
Откуда к нам пришли отрицательные числа? Сказка бабушки Тортилы Прямая пропорциональность и ее график
Прямая пропорциональность и ее график Решение задач на кратное сравнение чисел
Решение задач на кратное сравнение чисел Логика. Введение
Логика. Введение Средняя линия треугольника (8 класс)
Средняя линия треугольника (8 класс) Занимательная математика. 2 класс
Занимательная математика. 2 класс Презентация на тему РАЗЛОЖЕНИЕ НА ПРОСТЫЕ МНОЖИТЕЛИ
Презентация на тему РАЗЛОЖЕНИЕ НА ПРОСТЫЕ МНОЖИТЕЛИ  Комплексные числа и действия над ними
Комплексные числа и действия над ними Умножение натуральных чисел 5 класс
Умножение натуральных чисел 5 класс Презентация на тему Единицы массы. Тонна. Центнер (4 класс)
Презентация на тему Единицы массы. Тонна. Центнер (4 класс) 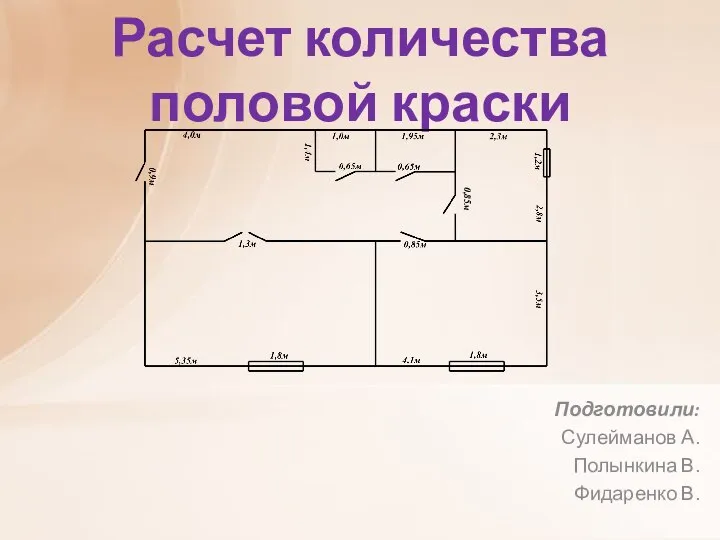 Расчет количества половой краски
Расчет количества половой краски Классическое определение вероятности
Классическое определение вероятности Длина окружности. Площадь круга
Длина окружности. Площадь круга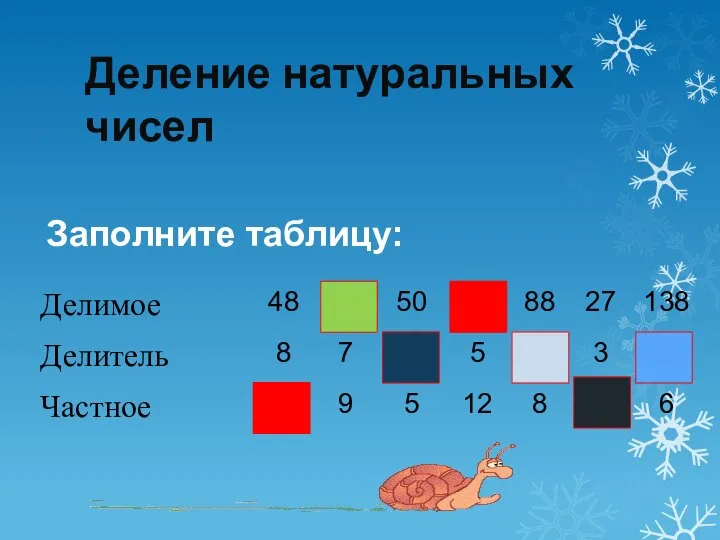 Деление натуральных чисел
Деление натуральных чисел Педагогические приемы включения детей, имеющих нарушения слуха, в образовательное пространство урока математики
Педагогические приемы включения детей, имеющих нарушения слуха, в образовательное пространство урока математики Презентация на тему Разность квадратов
Презентация на тему Разность квадратов  Дроби вокруг нас
Дроби вокруг нас Вычисление интегралов вида R(x, Jax2 + bx+c) dx
Вычисление интегралов вида R(x, Jax2 + bx+c) dx Алгебра логики
Алгебра логики Линейные операции над векторами
Линейные операции над векторами Анализ контрольной работы
Анализ контрольной работы