- Главная
- Математика
- Решение задачи по геометрии

Содержание
Слайд 3Решение
1)MO ┴(ABC),то MO ┴ BD (по определению ┴ прямой и плоскости).
2)MO┴(ABC)
Решение 1)MO ┴(ABC),то MO ┴ BD (по определению ┴ прямой и плоскости). 2)MO┴(ABC)

(ABC)┴(AMC)(по признаку ┴ плоскостей)
MOє(AMC)
3) (ABC)┴(AMC)
(ABC)⋂(AMC)=AC OB┴(AMC) (по св-ву плоскостей).
OB┴AC
4)d(B;(AMC)=OB
BD= √2*AB ; BD=8√2
OB=0,5*BD ; OB=4√2
Ответ: d(B;(AMC))=4√2
Следующая -
Задания к вебинару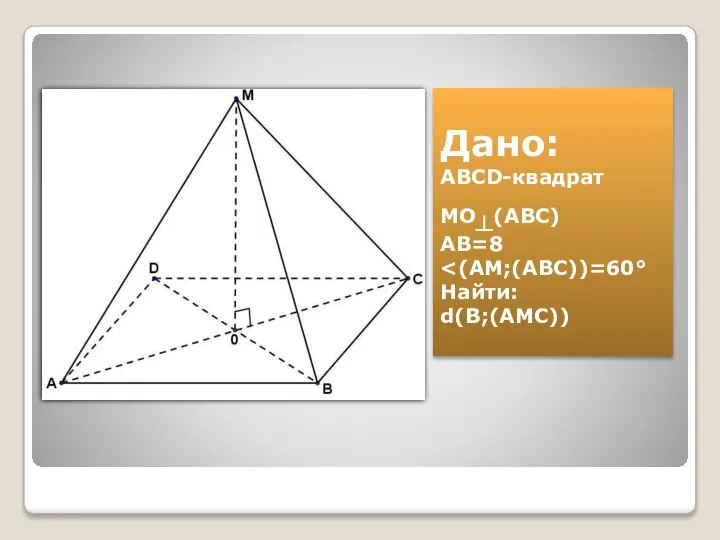
 Стандартный вид одночлена
Стандартный вид одночлена Системы показательных уравнений и неравенств
Системы показательных уравнений и неравенств Функции нескольких переменных
Функции нескольких переменных Геометрические тела и их изображение
Геометрические тела и их изображение Трёхчлен
Трёхчлен Синус, косинус и тангенс острого угла прямоугольного треугольника
Синус, косинус и тангенс острого угла прямоугольного треугольника Однородное уравнение повышенной сложности
Однородное уравнение повышенной сложности Построение перпендикуляра и параллельных прямых
Построение перпендикуляра и параллельных прямых Презентация на тему Графическое решение квадратных уравнений (8 класс)
Презентация на тему Графическое решение квадратных уравнений (8 класс)  Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3
Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3 Цилиндр
Цилиндр Презентация на тему Вклад Пифагора в развитие музыки 7 класс
Презентация на тему Вклад Пифагора в развитие музыки 7 класс  Квадрат. Свойства и признаки квадрата
Квадрат. Свойства и признаки квадрата Решение задач Коши с помощью matlab
Решение задач Коши с помощью matlab Тригонометрия – математическая дисциплина. Синус, косинус, тангенс и котангенс угла (10 класс)
Тригонометрия – математическая дисциплина. Синус, косинус, тангенс и котангенс угла (10 класс) Презентация на тему Начальные геометрические сведения
Презентация на тему Начальные геометрические сведения  Нахождение числа по его части. (6 класс. Тест №15)
Нахождение числа по его части. (6 класс. Тест №15) Равнобедренный треугольник
Равнобедренный треугольник Площадь. Площадь прямоугольника. 5 класс
Площадь. Площадь прямоугольника. 5 класс Геометрический смысл производной
Геометрический смысл производной Окружность. Математика, ЕГЭ
Окружность. Математика, ЕГЭ Загадки о цифрах
Загадки о цифрах Квадратный корень из степени. Подготовка к ОГЭ
Квадратный корень из степени. Подготовка к ОГЭ Статистические гипотезы и их проверка
Статистические гипотезы и их проверка Сокращение дробей. Графический диктант
Сокращение дробей. Графический диктант Арифметический пейзаж
Арифметический пейзаж Векторная алгебра. Векторы на плоскости и в трехмерном пространстве, линейные операции над ними
Векторная алгебра. Векторы на плоскости и в трехмерном пространстве, линейные операции над ними Сечение геометрических тел плоскостями
Сечение геометрических тел плоскостями