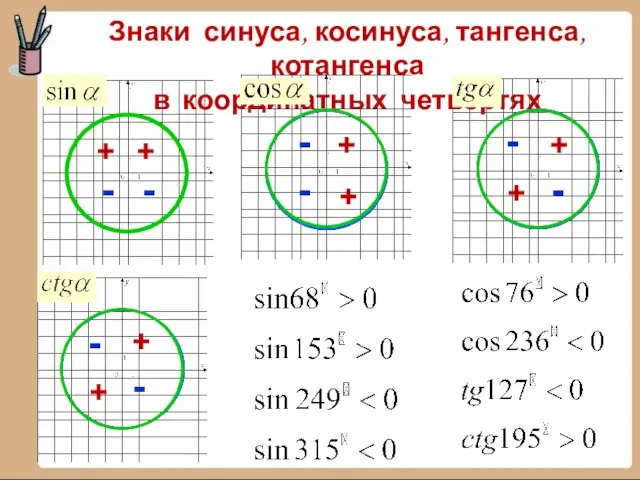
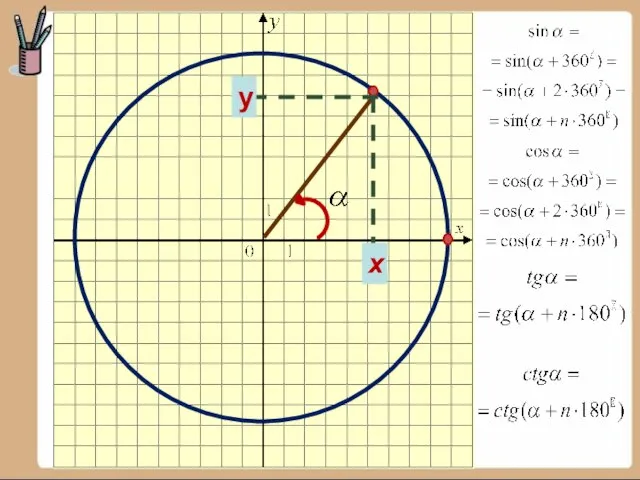
где n – целое число,
0<ά<1800.
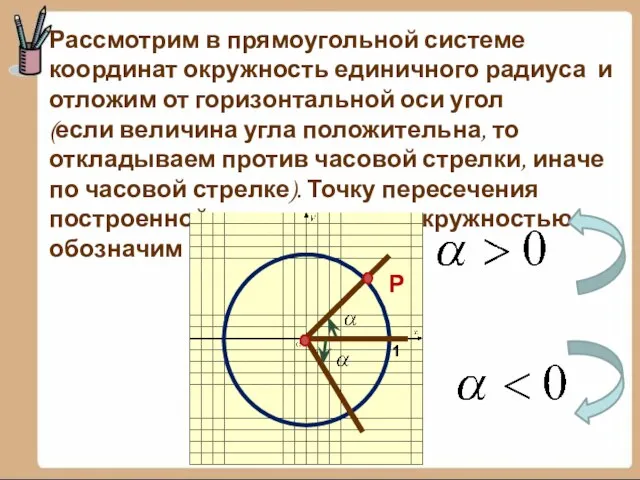
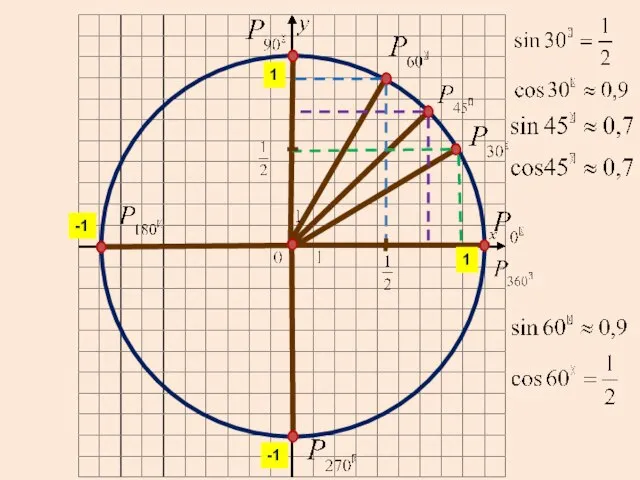
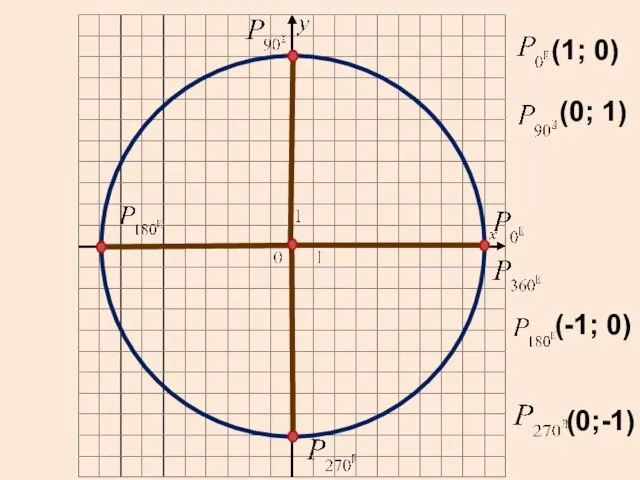
2. Точка Р – конечная точка поворота на 50о. Найдите наименьшее по модулю значение угла β, точки P1, которая получается из точки Р симметрией относительно оси ординат.
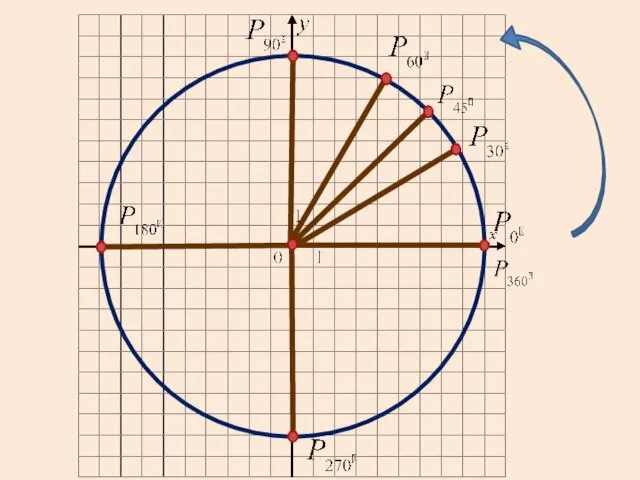
3. Переведите угол 150о из градусной меры в радианную.
4. Переведите угол 1,25π из радианной меры в градусную.
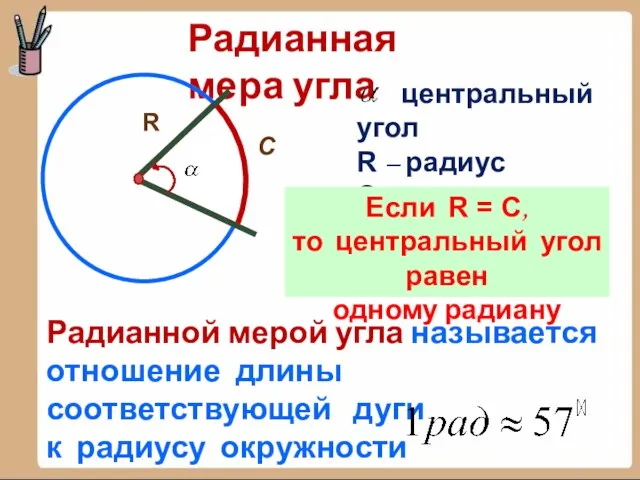
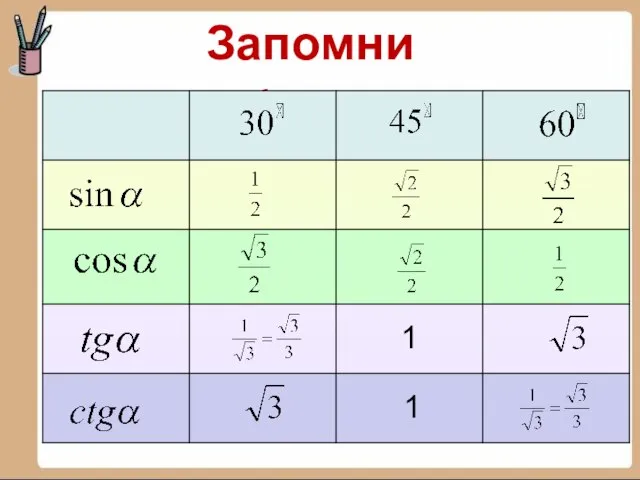
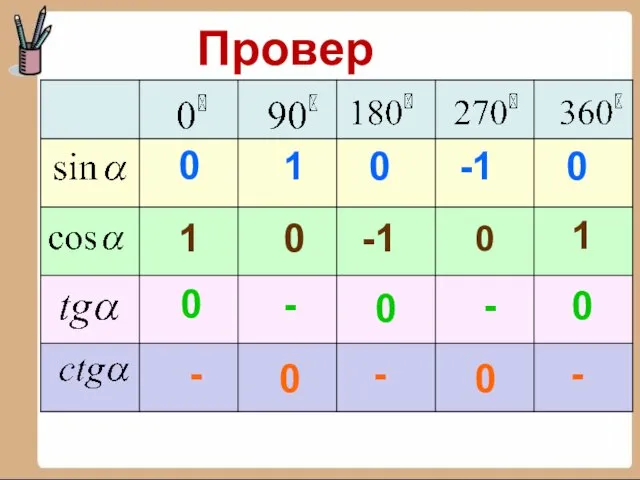
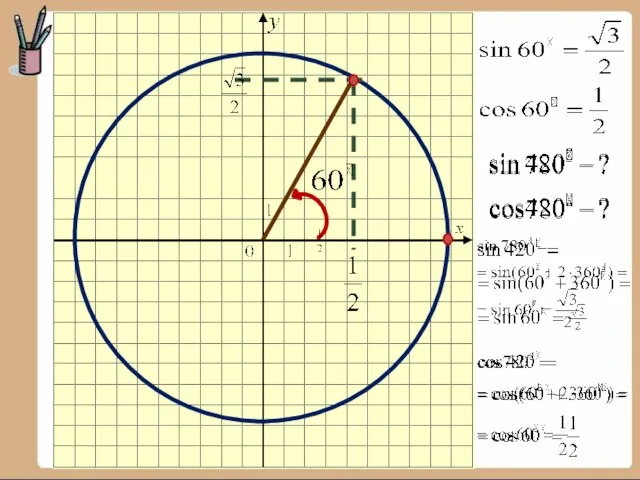
5. Допишите равенство ...0 =
6. Запишите формулу перехода от рад
к градусам.
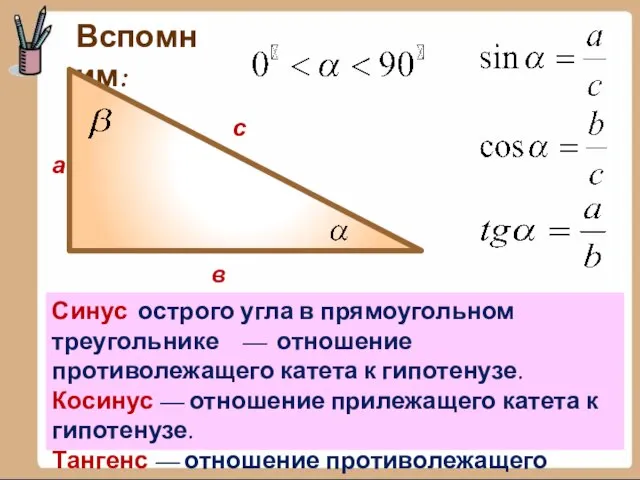
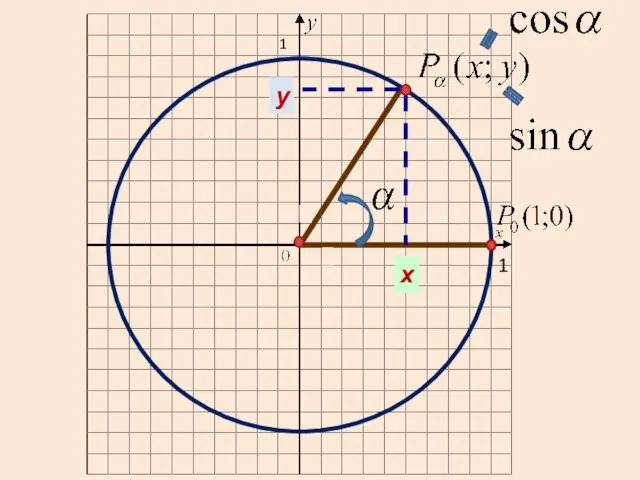
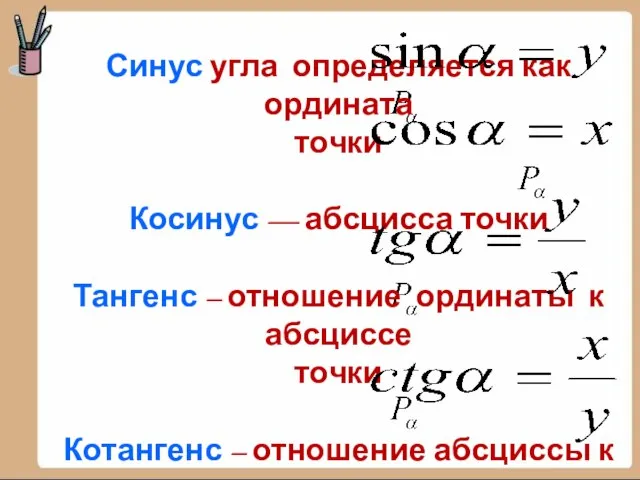
7. Запишите, как найти через стороны треугольника косинус угла ά. (рис)
Вариант 2
Представьте угол –710о в виде a° + 360°n, где n – целое число, 0<ά<180°.
2. Точка Р – конечная точка поворота на 50о. Найдите наименьшее по модулю значение угла β, точки P1 , которая получается из точки Р симметрией относительно оси абсцисс.
3. Переведите угол 135 о из градусной меры в радианную.
4. Переведите угол 2,5π из радианной меры в градусную.
5. Допишите равенство …0 =
6. Запишите формулу перехода от радиан к градусам.
7. Запишите, как найти через стороны треугольника синус угла ά.(рис)


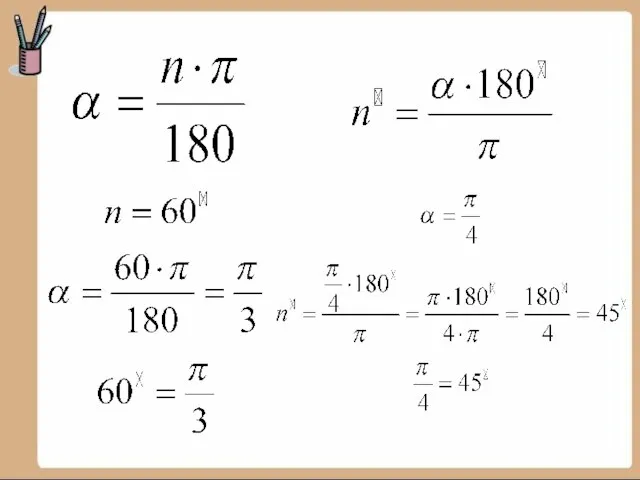








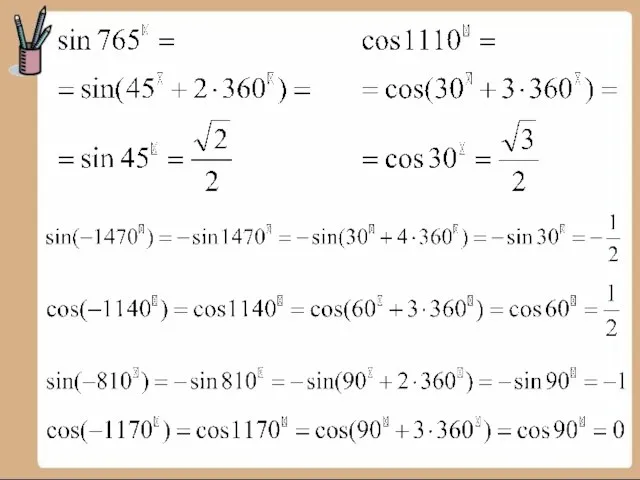
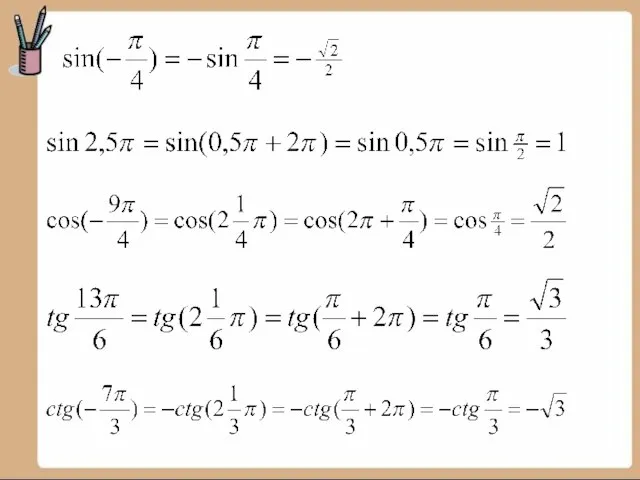

 Решение задач на применение признаков подобия треугольников
Решение задач на применение признаков подобия треугольников Классификация уровней понимания
Классификация уровней понимания Сложение и вычитание в пределах 1000
Сложение и вычитание в пределах 1000 Решение уравнений (урок 3). 6 класс
Решение уравнений (урок 3). 6 класс Деление чисел
Деление чисел Простые и составные числа (дистант)
Простые и составные числа (дистант) Числовой луч (1 класс)
Числовой луч (1 класс) Площадь параллелограмма
Площадь параллелограмма Основы математической статистики
Основы математической статистики Линейные пространства
Линейные пространства По следам телепередач. Поле чудес
По следам телепередач. Поле чудес Степень с отрицательным показателем
Степень с отрицательным показателем Занятие 45. Формулы двойного угла. Формулы половинного угла
Занятие 45. Формулы двойного угла. Формулы половинного угла Координати вектора. Модуль вектора
Координати вектора. Модуль вектора Множество. Элемент множества
Множество. Элемент множества Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ  Классификация треугольников
Классификация треугольников Объёмные фигуры и формулы нахождения объёма
Объёмные фигуры и формулы нахождения объёма Нахождение дроби от числа
Нахождение дроби от числа Сложение вида + 1, вычитание вида -1
Сложение вида + 1, вычитание вида -1 Системы массового обслуживания с отказом
Системы массового обслуживания с отказом Умножение обыкновенных дробей
Умножение обыкновенных дробей Система MatLab/ Методические указания к выполнению лабораторных работ
Система MatLab/ Методические указания к выполнению лабораторных работ Решение составных задач
Решение составных задач Наборы из нулей и единиц. Дискретный анализ. Лекция 2
Наборы из нулей и единиц. Дискретный анализ. Лекция 2 ВПР - 7- 9 класс
ВПР - 7- 9 класс Симметрия в пространстве. Уравнение Сферы
Симметрия в пространстве. Уравнение Сферы Финансовая грамотность
Финансовая грамотность