Робота учасника XVIII обласної математичної олімпіади Гарасюка Дмитра Андрійовича

Задача 1.1.1

1 спосіб
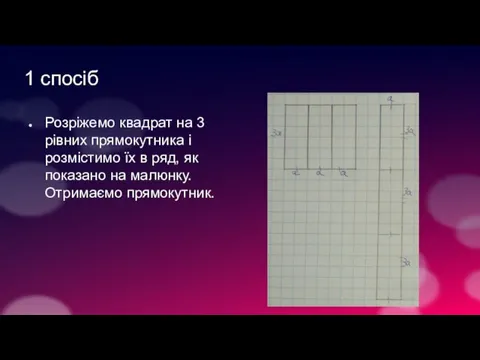
Розріжемо квадрат на 3 рівних прямокутника і розмістимо їх в ряд, як показано на малюнку. Отримаємо прямокутник.

2 спосіб
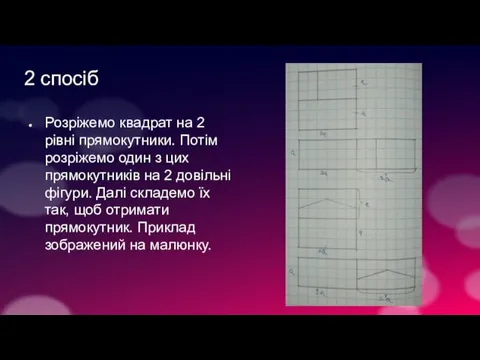
Розріжемо квадрат на 2 рівні прямокутники. Потім розріжемо один з цих прямокутників на 2 довільні фігури. Далі складемо їх так, щоб отримати прямокутник. Приклад зображений на малюнку.

3 спосіб
Проведемо діагональ квадрата. Потім з його 3 кута опустимо перпендикуляр на діагональ. Далі розмістимо фігури так, як на малюнку, і отримаємо прямокутник.

Задача 1.1.2

1 спосіб
Проведемо діагональ квадрата. Потім з протилежних вершин, до яких проведена діагональ, проведемо відрізки до протилежних сторін так, як показано на малюнку. Отримаємо 2 рівних прямокутних трикутника і 2 — тупопокутних.

2 спосіб
Проведемо діагональ квадрата. Потім з однієї з вершин, до яких проведена діагональ, проведемо відрізки до двох сусідніх сторін так, як показано на малюнку. Отримаємо 2 рівних прямокутних трикутника і 2 — тупопокутних.

Задача 1.2.1

1.2.1.2
Потрібно розділити 2 сторони трикутника навпіл, а 3 — на 3 частини у співвідношенні 1:2:1. Далі проводимо відрізки, як на малюнку і складаємо з отриманих фігур квадрат.

1.2.1.1
Ця задача є оберненою до 1.2.1.2, тому виконується аналогічно.

Задача 1.3

Для отримання трьох подібних, але не рівних прямокутника потрібно поділити квадрат так, як на малюнку, а співвідношення сторін ≈1,3247…

Задача 1.6.2

Заповнимо клітинки за таким правилом (приклад на малюнку):
1. Один рядок заповнюємо натуральними числами в порядку зростання справа наліво.
2. Другий рядок заповнюємо зліва направо.
Продовжуємо заповнювати таблицю, поки не залишиться порожньої клітинки. Ця закономірність була знайдена Карлом Гауссом.

Задача 2.1

Від кожної вершини квадрата на однаковій відстані відкладемо точки за часовою стрілкою ( проти часової). Далі сполучимо точки так, як на малюнку. Розглянемо 4 утворені прямокутні трикутники: вони рівні за 2 катетами. Отже, всі сторони утвореного чотирикутника рівні. α + β = 90°. Тоді γ = 180° - 90° = 90°. Отже, утворений чотирикутник- квадрат.