Рыцарский турнир

В начале XI вв. киевский князь создал систему пограничных крепостей на западе и юге своего государства, в том числе Хотин. Ее основным назначением была защита от всевозможных завоевателей.
Хотинская крепость

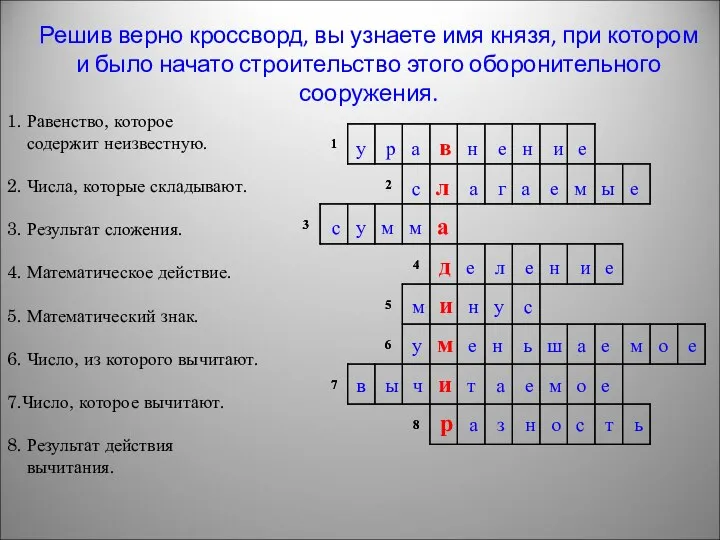
Решив верно кроссворд, вы узнаете имя князя, при котором и было начато строительство этого оборонительного сооружения.
1. Равенство, которое
содержит неизвестную.
2. Числа, которые складывают.
3. Результат сложения.
4. Математическое действие.
5. Математический знак.
6. Число, из которого вычитают.
7.Число, которое вычитают.
8. Результат действия
вычитания.
у р а в н е н и е
с л а г а е м ы е
с у м м а
д е л е н и е
м и н у с
у м е н ь ш а е м о е
в ы ч и т а е м о е
р а з н о с т ь

Именно при правлении князя Владимира Великого около 1000 лет назад для защиты страны от набегов завоевателей была построена Хотинская крепость.
Влади́мир I Святосла́вич (др.-рус. Володимѣръ Свѧтославичь, ок. 960 — 15 июля 1015) — киевский великий князь, при котором произошло крещение Руси.
Известен также как Владимир Святой, Владимир Креститель (в церковной истории) и Владимир Красное Солнышко (в былинах).

Рыцарями могут быть только сильные, ловкие, быстрые.
5
40
60

Заменив многоточие числами и разгадав шифр-код, вы узнаете имя князя, который занимался укреплением этой крепости от набегов монголо-татарских завоевателей
Г
К
Л
И
И
Й
А
Ц

Дании́л Рома́нович Га́лицкий (1201, по др. данным 1204[1] —1264) — князь Волынский (1205—1206, 1215—1231), Галицкий (1205—1206, 1211—1212, 1229—1231, 1233—1235, 1238—1254), 1-й король Галицкой Руси (1254—1264), великий князь Киевский (1240), политический деятель, дипломат и полководец, сын князя Романа Мстиславича, из галицкой ветви рода Рюриковичей.

«Рыцарская» физкультминутка
Посмотри, мой милый друг,
Что находится вокруг:
Небо светло-голубое
Солнце светит золотое,
Ветер листьями играет,
Тучка в небе проплывает.
Поле, речка и трава.
Горы, воздух и листва,
Птицы, звери и леса,
Гром, туманы и роса,
Человек и время года –
это всё вокруг природа.

«Рыцарское лото»
50
3
120
14
10
400
20
Именно такую площадь в 20 га первоначально занимала Хотинская крепость
v = 10 м/с, t = 5 с, s = ?
v = 5 км/ч, s = 15 км, t = ?
а = 6 см, b = 20 см, S = ?
а = 4 см, b = 3 см, P = ?
5. Р = 120 м, а = ?
6. а = 20 м, S = ?
7. а = 20 м, P = ?
80
8. s = 200 м, t = 20 с, v = ?
30

3 0 4
4 5 3
1 2
1
*
*
7
*
6
*
1
заменить звездочки пропущенными цифрами
В 1621 году у стен крепости проис-ходили события знаменитой Хотинской войны, которая просла-вила запорожских казаков.
9 5
7 3
3 9
*
6
*
8
*
7
*
1
Великий российский ученый Михаил Ломоносов, восхищаясь мужеством своих соотечественников, написал «Оду на победу над турками и татарами и на взятие Хотина 1739 года».