Проверка статистических гипотез. Версия 2

Определение
Статистическая гипотеза – утверждение о свойствах распределения вероятностей случайной величины (или случайного вектора).
Гипотеза нуждается в проверке.
Проверка основывается на результатах эксперимента, на наблюдениях.

Напоминание
Что такое функция распределения?
Что такое плотность распределения?

Раздел 1
Зачем проверяют
статистические гипотезы
Обсудим наиболее важные статистические гипотезы.

1. Гипотеза согласия.
Обозначим функцию распределения случайной величины Х.
Пусть - некоторая заданная функция распределения.
Гипотеза : функции распределения совпадают, то есть =
Кому и когда приходится проверять гипотезу согласия?

Пример гипотезы согласия
Гипотеза о нормальности распределения
В этом случае

Почему гипотеза нормальности важна?
1. Нормальное распределение часто встречается
(вспомним центральную предельную теорему).

Почему гипотеза нормальности важна?
2. Когда распределение нормальное, экономим деньги: если
А) распределение можно считать нормальным и
Б) задана необходимая погрешность результата,
то при проведении анализа можно обойтись меньшим числом наблюдений.
Например, опросить меньше покупателей.

Пример гипотезы согласия 2
Гипотеза об экспоненциальности распределения.
В этом случае функция распределения

Почему важна гипотеза экспоненциальности?
Экспоненциальное распределение часто встречается, когда изучается «время ожидания».

Например,
Время до аварии (нужно для расчета страховой премии).
Время обслуживания покупателя кассиром (нужно для определения числа касс в супермаркете).
Время до поломки изделия (нужно для планирования расходов на гарантийный ремонт).

2. Гипотеза однородности.
Обозначим функцию распределения случайной величины Х.
Обозначим функцию распределения случайной величины Y
Гипотеза : функции распределения совпадают
Кому и когда приходится проверять гипотезу согласия?

Например,
Распределение продаж до рекламной акции и после нее.
Если распределение продаж не изменилось, то улучшения нет.
Может сравниваться распределение покупателей по возрасту. Например, если реклама была нацелена на конкретный сегмент, например, на молодых мам.

3. Гипотеза независимости.
Гипотеза : случайные величины X и Y независимы
Кому и когда приходится проверять гипотезу независимости?

Например,
Если возраст покупателей и объем покупки зависимы, то возраст надо учитывать при сегментации покупателей.
Иногда зависимость бывает неочевидной.
Длина волос и рост людей – зависимые переменные.

Вопрос:
наличие балкона влияет на цену квартиры?

На шаг дальше…
В эконометрике редко интересен сам факт зависимости. Обычно идут дальше, пытаются описать зависимость.
Подобные задачи решаются, в частности, методами регрессионного анализа.
Регрессионный анализ – сдедующая тема.

4. Гипотезы о параметре распределения.
Очень часто не так важно распределение случайной величины. Интересна лишь одна характеристика распределения.

Если анализируются продажи магазина, то в первую очередь интересно…
Математическое ожидание
Так как математическое ожидание – вероятностная модель для среднего значения.
В данном случае для средних продаж.

Гипотеза. Математические ожидания случайных величин X и Y одинаковы.
EX = EY

Если сравниваются медианы:
Гипотеза. Медианы случайных величин X и Y одинаковы.
Med(X) = med(Y)

Основные условия применения статистических тестов
Вопрос должен касаться какой-либо характеристики массового явления.
Характеристика меняется случайным образом от наблюдения к наблюдению.
Вопрос должен быть относительно простым и четко сформулированным

Пример 1
В обычных условиях зафиксирован некоторый уровень продаж. Затем была проведена рекламная акция.
Руководству фирмы надо оценить результат.
Для этого нужно выяснить, было ли существенное увеличение продаж. В частности, окупились ли затраты на рекламу.

Основная проблема:
Увеличение продаж могло быть вызвано случайными факторами.
Продажи все время меняются, случайным образом отклоняются от заданного значения.
Статистически значимое отклонение должно превышать эти случайные отклонения.

Пример 2
Разработан новый варианта упаковки товара.
Требуется проверить предположение, что товар в новой упаковке имеет в данном регионе больший уровень продаж, чем вариант в старой упаковке.

Пример 3
Верно ли, что основной конкурент действует на том же сегменте рынка, что и фирма «Х»?
При ответе на этот вопрос может потребоваться проверить, одинаково ли распределение по возрасту у покупателей товаров фирмы «Х» и ее основного конкурента.

Пример 4
Фирма изучает постоянных покупателей своей продукции, чтобы увеличить их лояльность и количество.
В рамках этой задачи аналитик проверяет, зависит ли лояльность потребителя от его пола, возраста, уровня образования.

Пример 4. Часть 2
Статистическая формулировка: проверить гипотезы о независимости уровня лояльности и
а) пола покупателя;
б) возраста покупателя;
в) уровня образования покупателя.
Далее, можно проверить, различаются ли средние значения изучаемых показателей у лояльных и не лояльных покупателей.

Раздел 2
Технологии проверки статистических гипотез
Основные понятия

Выбираем из двух гипотез!
Гипотеза принимается или отвергается
Так неудобно
Надо: выбираем между двумя статистическими гипотезами.

Определение
Проверку гипотез на основе выборочных статистических данных называют статистической проверкой гипотез.

Основная и альтернативная гипотезы
Одну из гипотез называют основной и обозначают, как правило, Н, а другую — альтернативной (конкурирующей) и обозначают К.
Если не уточняется, о какой гипотеза идет речь, то имеется в виду основная гипотеза.
Чаще всего (но не всегда) одна гипотеза утверждает, что предположение верно, другая – что нет.

Неточно говорить «…выбрана основная гипотеза…» или «…выбрана альтернативная гипотеза…»,
Неточно говорить
«…основная гипотеза принята…» или «основная гипотеза отвергнута…».

Важное уточнение.
Правильно говорить
«основная гипотеза отвергнута…» и
«основная гипотеза не отвергнута…».
Так как обычно проверяют лишь достаточное условие.

Комментарий 1:
Гипотеза: число делится на 6 нацело.
Фактически проверяем, делится ли число на 2 нацело.

Комментарий 2:
Часто случается, что у аналитика недостаточно данных, чтобы проявился изучаемый эффект.
Например,
фармацевтическая компания выпускает лекарство, аналогичное уже существующему, так называемый "дженерик" (generic) вместо оригинального, производимого разработчиком ("brand-named").
Компания проводит исследование, проверяющее, что лекарство-аналог эквивалентно уже существующему.

Отвергнуть гипотезу недостаточно
Основная гипотеза при анализе: отличия между лекарствами нет.
Дело касается здоровья людей, и не отвергнуть гипотезу недостаточно.
Необходимы более жесткие требования к процедуре. Надо проверить еще и побочные эффекты у лиц страдающих заболеванием «х1», «х2», и так далее…

Вывод
Хотя часто можно услышать, что (основная) гипотеза принята, такое выражение неточно.
Точнее говорить, что (основная) гипотеза не отвергнута

Ошибки первого и второго рода
Ошибка первого рода состоит в том, что отвергается основная гипотеза, когда на самом деле она верна.
Ошибка второго рода состоит в том, что отвергается конкурирующая гипотеза, когда она верна.

Аналогия
В больнице врач принимает решение, направлять пациента на операцию, или нет.

Когда врач делает ошибку первого рода?
Когда врач делает ошибку второго рода?

Гипотеза: нужна срочная операция

Может ли врач свести частоту (вероятность) ошибок первого рода к нулю?
Может ли врач свести частоту (вероятность) ошибок второго рода к нулю?

Есть исключения
Например,
если мы будем вакцинацию считать операцией,
то получается, что врачи предпочитают делать маленькую "превентивную" операцию всем, чтобы исключить ошибки первого рода.

Последствия ошибок могут быть различными
Ошибка первого рода (обычно) опаснее, но полностью избежать ее не удастся.
При проверке статистических гипотез исходят именно из этой предпосылки

Уровень значимости
Долю ошибок первого рода ограничивают сверху числом, называемым уровень значимости.
Исторически сложилось так, что в качестве уровня значимости чаще всего выбирают одно из чисел 0.005, 0.01, 0.05.
То есть аналитик допускает, что (в среднем) одна проверка из 200, 100, 20 будет давать неверный результат.

Для новичков!
Чаще всего уровень значимости равен 0,05
На самом деле выбор уровня значимости – большая проблема! Зависит, например, от числа наблюдений!
Смотрите литературу

«медицинский» пример
На что влияет выбор уровня значимости?
Проектирование атомной электростанции
Трелевочный трактор

Ошибка второго рода и мощность
Как добиться того, чтобы вероятность ошибки второго рода была малой?
Очень сложно.
Состоятельные критерии.
Ошибку можно уменьшить, если увеличить число анализируемых наблюдений.
Необходимы большие выборки.

Дополнительно
Если выборка маленькая (часто границей между большой и маленькой выборкой рекомендуют считать 30 наблюдений), проверить гипотезу по малой выборке удастся.
Но
Платой за малый размер будет неприемлемо большая вероятность ошибки второго рода.
Большинство практиков игнорируют ошибку второго рода.
Это неверно.
Профессиональные статистики в таких ситуациях часто увеличивают уровень значимости (например до 0.15 или 0.2), чтобы сделать вероятности ошибок сопоставимыми.

Задача.
Вместо врача рассмотрим банковского служащего, принимающего решение, выдавать заем или нет.
Как будут интерпретироваться статистические понятия в этом случае?

Алгоритм проверки статистических гипотез
1. Имеются n наблюдений , то есть n чисел, полученных, например, в результате опроса.
2. Заранее задан уровень значимости α. Обычно это одно из чисел 0.005, 0.01, 0.05.

3. Задан статистический критерий, то есть функция от наблюдений .
4. Найдено p-значение (p-value).
Иногда переводится как значимость (Significance).

5. Проверяются все условия, при которых критерий будет работать.
Условия – Из учебника или справочника.
Несколько важных критериев будет рассмотрено далее

6.
Если p< α - гипотезу отвергаем, если p> α - не отвергаем.
Напомним:
α – уровень значимости
p - p-value.

Комментарии
Наблюдения не обязательно являются числами.
Выбор того статистического критерия, который подходит для задачи – важная и сложная задача

Проверка условий применимости
Например, для применения t – критерия Стьюдента или для проверка гипотезы независимости с помощью критерия Пирсона надо проверить близость распределения переменных к нормальному.

Статистика критерия или
тестовая статистикой
Иногда используют статистику критерия или тестовую статистику.
Изредка она важна сама по себе (например, коэффициент корреляции), в таких конкретных случаях мы будем ее указывать.

Интерпретация статистики критерия
Значение статистики критерия (обычно) измеряет, насколько данные согласуются с гипотезой.

"Маленькие" значения статистики критерия указывают, что данные «ведут себя» в соответствии с гипотезой.
В этом случае гипотеза не отвергается.

"Большие" значения статистики критерия указывают, что данные не соответствуют гипотезе, противоречат ей.
Гипотеза отвергается.

Пример
Нормальное распределение с дисперсией 1
Имеется n наблюдений
Основная гипотеза: математическое ожидание равно 11
Альтернативная гипотеза: математическое ожидание равно 12

Напоминание из теории вероятностей
Среднее арифметическое n независимых одинаково распределенных случайных величин с общим нормальным распределением N(a, b) имеет нормальное распределение N(a, b/n)

Вопрос:
Где на графике ошибка первого рода, где ошибка второго рода?

Интерпретация статистики критерия
В статистике существует традиция, что именно задавать в качестве основной гипотезы.
Примеры.

Раздел 3
Важные частные случаи

Проверка гипотезы о нормальности распределения случайной величины

Статистическая формулировка
Гипотеза: Случайная величина имеет нормальное распределение, значения параметров распределения заранее не известны.
Конкурирующая гипотеза: Распределение случайной величины отличается от нормального.

Критерий Шапиро-Уилка
Критерий Шапиро-Уилка.
shapiro.test(data)
От 3 до 5000 наблюдений

Package "nortest"
Критерий Anderson-Darling
library(nortest)
ad.test(data)
Критерий Lilliefors (Kolmogorov-Smirnov)
library(nortest)
lillie.test(x)

Число наблюдений
Если анализируется меньше 60 (2000) наблюдений, рекомендуется использовать критерий Шапиро-Уилка
если больше 60, то критерий Колмогорова-Смирнова.

А нужно ли проверять гипотезу нормальности?

Как оказалось, для тех методов, которые рассматриваются в курсе, требование нормальности распределения можно заметно ослабить.
Эти методы работают не только когда переменные имеют нормальное распределение, но и когда, как говорят, «распределение данных несущественно отличается от нормального».

допустим известно, что распределение случайной величины не нормальное.
В каком случае отклонение от нормальности не существенное?

Итак,
гипотеза о нормальности распределения изучаемой переменной уже отвергнута.

Существенные отклонения
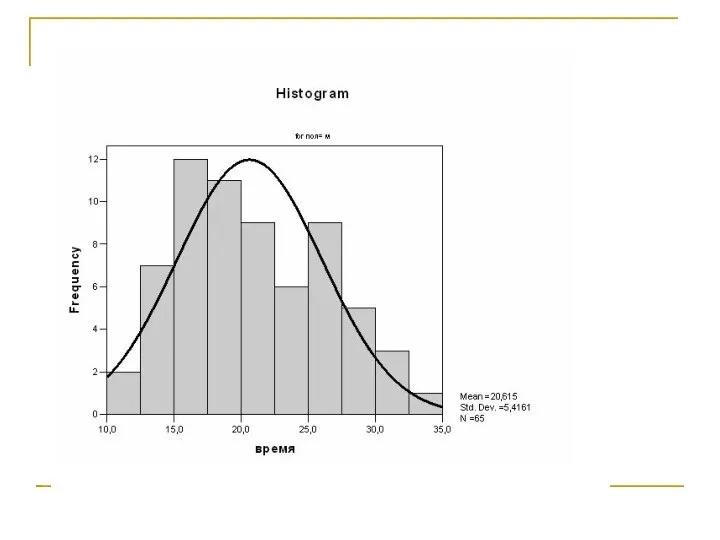
1. Наличие выбросов в данных.
2. Явная асимметрия гистограммы.
3. Очень сильное отклонение формы гистограммы от колоколообразной формы.

Рекомендуется
строго относиться к присутствию выбросов,
снисходительно к отклонениям от симметрии.
Наше отношение к колоколообразной форме гистограммы зависит от числа наблюдений. Если имеется меньше 30 наблюдений, наше отношение в высшей степени либерально, если число наблюдений находится между 30 и 150, мы относимся к отклонениям снисходительно, если имеется больше 150 наблюдений – строго.

Лекарство
Иногда оно опаснее болезни...
Выбросы — удаляем (осторожно!)
Асимметрия — преобразуем данные (например, логарифмируем, или преобразование Бокса-Кокса)
Бимодальность — разбиваем выборку на подвыборки

Пример 1
Население городов России в 1959 году
Исходные данные
Логарифм населения

Пример 2
Альбукерк – продажи домов

Сравнение центров распределений

Сравнение центров распределений
Центр распределения - то одно единственное число, которое описывало, характеризовало бы выборку.
В качестве центра чаще всего используют среднее арифметическое, медиану или усеченное среднее.

Другие методы
оценки центра распределения
Andrews; Bickel; Hampel; Huber; Rogers, Tukey.
Robust estimates of location: survey and advances.
1972 Princeton University Press

Среднее арифметическое или медиана?
Если распределение хотя бы одной из выборок существенно отличается от нормального, в качестве центра предлагается использовать медиану.
В остальных случаях, то есть если распределение каждой выборки можно считать нормальным или несущественно отличающимся от нормального, в качестве центра предлагается использовать среднее арифметическое.

Выбор центра распределения
Если центром распределения выбрана медиана, центры сравниваются с помощью критерия Манна – Уитни-Вилкоксона.
Если центром распределения выбрано среднее арифметическое, центры сравниваются с помощью одной из версий критерия Стьюдента.

Примеры
Обучение менеджеров
Магазины

Парные и независимые выборки
В случае парных выборок имеются пары наблюдений (измерений) одного и того же объекта.
Вариант: пары измерений делались в один и тот же момент.

Независимые выборки
В случае независимых выборок каждое наблюдение соответствует отдельному объекту, т.е. измеряются разные объекты.
Принадлежность объектов выборкам определяется по значениям дополнительной группирующей переменной.

Независимые и парные выборки
Если выборки парные, используется опция paired = TRUE.
Если выборки независимые, используется опция paired = FALSE.

Примеры
Время в магазинах
Альбукерк

Сравнение медиан выборок
Гипотеза: Медианы равны.
Альтернативная гипотеза: Медианы различаются.

Статистика критерия Манна-Уитни U
U1 = n1*n2 + {n1 * (n1 + 1)/2} — T1
U2 = n1*n2 + {n2 * (n2 + 1)/2} — T2
U = min(U1, U2)
Ti — сумма рангов в объединенной выборке наблюдений из выборки i
n1 и n2 — размеры выборок

Статистика критерия Манна-Уитни
идея метода
Обозначим одну выборку x, другую y.
Для каждого наблюдения из выборки x сосчитаем число тех наблюдений в выборке y, которые меньше его. (Для нагладности, пока считаем, что совпадений нет).
Сложим все полученные числа.

Важно!
Критерий Манна-Уитни проверяет не равенство медиан, а другое утверждение.
Имеются две выборки наблюдений случайных величин Х и Y.
Гипотеза: Случайные величины X и Y таковы, что P{X>Y}=1/2.
Альтернативная гипотеза: Случайные величины X и Y таковы, что P{X>Y}≠1/2.
Для практических целей различие, тем не менее, несущественно

Under more strict assumptions than those above, e.g., if the responses are assumed to be continuous and the alternative is restricted to a shift in location (i.e. F1(x) = F2(x + δ)), we can interpret a significant MWW test as showing a difference in medians.

Критерий
Манна-Уитни-Вилкоксона
wilcox.test(x, y,
alternative = "two.sided",
paired = FALSE, exact = TRUE,
correct = FALSE)

Примеры
Время в магазинах
Альбукерк

Сравнение средних значений выборок
Гипотеза: Математические ожидания равны.
Альтернативная гипотеза: Математические ожидания различны.

T-критерий Стьюдента
t.test(x, y, alternative = "two.sided", paired = FALSE, var.equal = FALSE)

Выбор статистического критерия
Если выборки парные, рекомендуется использовать парный t-критерий Стьюдента.
Если выборки независимые, рекомендуется использовать t-критерий Стьюдента для 2-х независимых выборок.

Надо еще сравнить дисперсии - 1
Метод 1
F-test of equality of variances
Не рекомендуется, слишком чувствителен к отклонениям от нормальности. См.
http://en.wikipedia.org/wiki/F-test_of_equality_of_variances
var.test(x, y)

Надо еще сравнить дисперсии - 2
Метод 2
Bartlett's test
Если данные нормально распределены, лучший вариант.
Не рекомендуется: чувствителен к отклонениям от нормальности;
Если данные не нормальны, часто дает "false positive" результат.

Надо еще сравнить дисперсии - 2
Метод 2
Bartlett's test
bartlett.test(x, g, data=data.table)
bartlett.test(x~g, data=data.table)

Надо еще сравнить дисперсии - 3
Levene's test
Критерий Ливиня/Левена
Содержится в пакете car

Надо еще сравнить дисперсии - 3
Levene's test
library(car)
leveneTest(x~g, data=data.table)

Надо еще сравнить дисперсии - 4
Fligner-Killeen test
Робастный, рекомендуется.
Хотя есть еще Brown-Forsythe test, возможно он еще лучше...

Надо еще сравнить дисперсии - 4
Fligner-Killeen test
fligner.test(x~g, data=data.table)

Примеры
Время в магазинах
Альбукерк

Гипотеза независимости
Основная гипотеза:
Случайные величины X и Y независимы
Альтернативная гипотеза:
Случайные величины X и Y зависимы

На практике:
Отвечаем на вопрос: переменная X влияет на переменную Y?

Комментарий
Если неизвестно, что на что влияет:
X на Y или
Y на X
статистический критерий не поможет!

Пример Бернарда Шоу

Диаграмма рассеивания
Иногда пишут - диаграмма рассеяния
Пример – швейцарские банкноты.

Зависимость -1
X – в количественной шкале
Y – в количественной шкале
Применяется коэффициент корреляции Пирсона
Или Спирмена
Иногда - Кендалла

Функциональная зависимость

Статистическая зависимость
двух переменных
Обобщение функциональной зависимости.
Одному и тому же значению x могут соответствовать разные значения y.
Например, один и тот же товар (например, телефон) может продаваться в разных магазинах по разной цене, то есть одному и тому же товару соответствуют разные цены.

статистическая зависимость
Определение статистическая зависимость – это функциональная зависимость СРЕДНЕГО значения переменной y от значения переменной x.
Откуда появляется среднее значение? Проводятся эксперименты (или наблюдается явление) при одном и том же значении x, при этом регистрируются разные значения y, затем эти значения усредняются.
На практике не всегда заметно, что одному и тому же значению переменной x может соответствовать много значений y, например когда повторные наблюдения при одном значении x не делались.

среднее значение переменной y равно натуральному логарифму значения x.

среднее значение переменной y равно натуральному логарифму значения x.

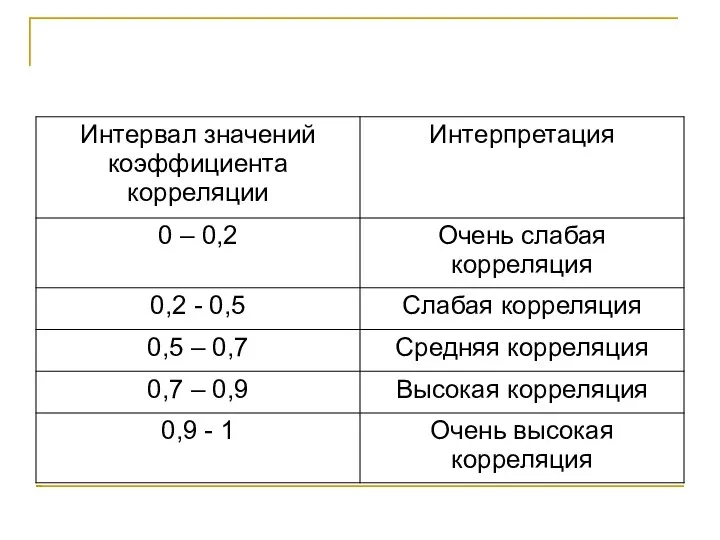
Коэффициент корреляции как «градусник», измеряющий степень зависимости
Формула для коэффициента корреляции

Выбор коэффициента
Если распределение каждой переменной несущественно отличается от нормального, применяется коэффициент корреляции Пирсона
В остальных случаях - коэффициент корреляции Спирмена
Вместо коэффициента корреляции Спирмена используют коэффициент корреляции Кендалла

Как проявляется зависимость на диаграмме рассеивания

Коэффициент корреляции равен 1

Коэффициент корреляции равен 0.9

Коэффициент корреляции равен 0.8

Коэффициент корреляции равен 0.6

Коэффициент корреляции равен 0.4

Коэффициент корреляции равен 0.2

Коэффициент корреляции равен 0.

Проблемы и ошибки при использовании коэффициента корреляции

Данные без выброса
коэффициент корреляции равен -0.81

Добавлен выброс в точке (10,10). Коэффициент корреляции упал до -0,55.

Выброс сдвинут в точку (18,5, 18,5) Коэффициент равен 0

Выброс сдвинут в точку (53, 53). Корреляция равна +0,81

Ложная корреляция

Зависимость -2
X – в количественной шкале
Y – в номинальной шкале
Сравниваем средние или медианы в группах
Или перекодируем количественную переменную, переводим ее в номинальную шкалу

Зависимость -3
X – в порядковой шкале
Y – в порядковой шкале
Используем коэффициент корреляции Спирмена
Или Кендалла

Зависимость -4
X – в номинальной шкале
Y – в номинальной шкале
Таблица сопряженности и критерий χ²

Критерий хи-квадрат
Формула для статистики

Статистика хи-квадрат как коэффициент корреляции
Коэффициент Пирсона
Коэффициент Чупрова

Примеры типичных ошибок при использовании критерия хи-квадрат

Пример 1
Действительно ли использование Internet связано с полом?
Все опрошенные пользуются Интернетом. Тех из них, кто использует Интернет пять часов в месяц или меньше, отнесли к мало пользующимся, остальных – к активным пользователям.

Пример 1
sex = пол.
Кодировка: "1" – мужчина, "0" – женщина.
internet = использование Internet.
Кодировка: "0" – использует мало, "1" – использует активно.
Имеется 30 наблюдений (опрошенных).

Пример 1

Пример 2
В результате изучения связи между покупкой модной одежды и семейным положением получены, среди прочих, следующие данные.
Имеется 1000 наблюдений (опрошенных).

Пример 2
Переменные.
sex = пол.
Кодировка: "1" – мужчина, "0" – женщина.
marriage = семейное положение.
Кодировка: "1" – женат/замужем, "0" – не женат/не замужем.
fashion = покупка модной одежды.
Кодировка: "0" – покупает мало, "1" – покупает много.

Пример 2

Пример 2

Пример 2

Пример 3
Маркетолог проводит исследование для рекламного агентства, разрабатывающего рекламу для автомобилей стоимостью свыше 30 тысяч долларов.
Он пытается проанализировать факторы, влияющие на владение дорогими автомобилями.

Пример 3
Переменные.
high_edu = образование.
Кодировка: "1" – высшее образование, "0" – нет высшего образования.
expe_car = наличие дорогого автомобиля.
Кодировка: "0" – дорогого автомобиля нет, "1" – дорогой автомобиль есть.
income = доход.
Кодировка: "0" – низкий доход, "1" – высокий доход.
Имеется 1000 наблюдений (опрошенных).

Пример 3

Пример 3

Пример 3

Пример 4
Маркетолог, исследующий сферу туристических поездок за границу, предположил, что на желание путешествовать влияет возраст.
Имеющиеся в его распоряжении данные содержат, среди прочего, следующую информацию.

Пример 4
Переменные.
desire = желание совершить путешествие за границу.
Кодировка: "1" – желание есть, "0" – желания нет.
sex = пол.
Кодировка: "0" – женщина, "1" – мужчина.
age = возраст.
Кодировка: "0" –до 45 лет, "1" – 45 лет или старше.
Имеется 1000 наблюдений (опрошенных).

Пример 4

Пример 4

Пример 4

Пример 4

Пример 5
Результаты анкетирования о проведении семейного досуга содержат, среди прочего, следующую информацию.
Переменные.
fastfood = частота посещения ресторанов быстрого питания.
Кодировка: "1" – часто, "0" – редко.
income = доход семьи.
Кодировка: "1" – высокий, "0" – низкий.
family = размер семьи.
Кодировка: "1" – большая семья, "0" – малая семья.

Пример 5

Пример 5