Слайд 2Повторение:
Расстояние – это длина от одного пункта до другого.
Большие расстояния, в основном, измеряются в

метрах и километрах.
Расстояние обозначается латинской буквой S.
Чтобы найти расстояние, надо скорость умножить на время движения:
S = v ∙ t
Слайд 3Повторение:
Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается

1 час, 1 минута или 1 секунда.
Скорость обозначается латинской буквой v.
Чтобы найти скорость, нужно расстояние разделить на время движения:
v = S : t
Слайд 4Повторение:
Время – это продолжительность каких-то действий, событий.
Время движения обозначается маленькой латинской буквой t.
Чтобы найти

время, нужно расстояние разделить на скорость движения:
t = S : v
Слайд 5Задача 1
Собственная скорость теплохода 27км/ч, скорость течения реки 3 км/ч. Сколько времени

затратит теплоход на путь по течению реки между двумя причалами, если расстояние между ними 120 км?
Слайд 6Решение:
1) v по течению= v собственная + v течения
27 + 3

= 30 (км/ч).
2) t по течению= s : v по течению
120 : 30 = 4 (ч.)
Ответ: 4 часа
Слайд 7Задача 2
Катер, имеющий собственную скорость 15 км/ч, проплыл 2 часа по течению

реки и 3часа против течения. Какое расстояние проплыл катер за все время, если скорость течения реки 2 км/ч?
Слайд 8Решение:
v по течению = v собственная + v течения
15 + 2

= 17 (км/ч.)
2) v против течения = v собственная – v течения
15 – 2 = 13 (км/ч.)
3) s по течению = v по течения · t по течения
17 · 2 = 34 (км)
4) s против течению = v против течения · t против течения
13 · 3 = 39 (км)
5) s = s по течению + s против течения
34 + 39 = 73 (км)
Ответ: 73 км
Слайд 9Вопросы:
Что такое собственная скорость катера?
Что такое скорость течения?
Как определяется

скорость катера по течению реки?
Как определяется скорость катера против течения?
Как определяется скорость движения плота по реке?
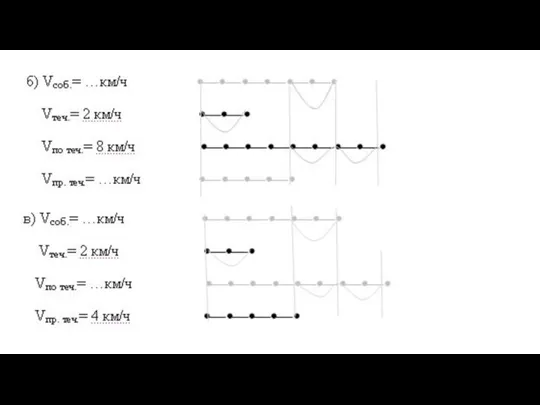
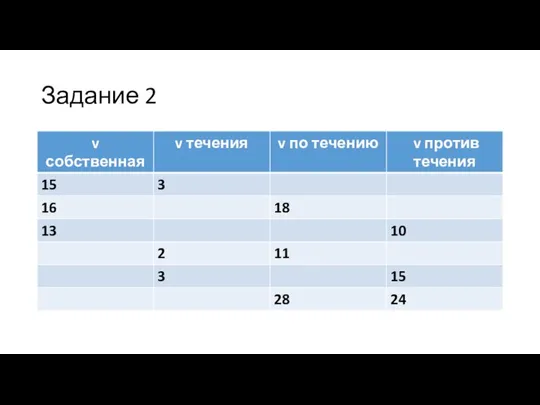
Слайд 10Задание 1
Из четырех скоростей (v собственная, v по течению, v против течения,

v течения) две заданы и изображены отрезком. Вычислите две другие скорости и изобразите их отрезками:
Слайд 14Задача 3
Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки.

Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?
Слайд 15Скорость сближения
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за

единицу времени.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Слайд 16Скорость удаления
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя

объектами, двигающимися в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Слайд 17Задача 4
Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость

первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
Слайд 18Задача 5
С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость

теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?
Слайд 19Задача 6
Из города в одном и том же направлении выехали легковой автомобиль

и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?
Слайд 20Задача 7
Пусть на одной улице имеется дом, школа и аттракцион. Дом находится

на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?

















 Число 8
Число 8 be798f8c4ede43fcabd1090e739d523d
be798f8c4ede43fcabd1090e739d523d Классическая формула подсчета результатов
Классическая формула подсчета результатов Формулы для радиусов вписанной и описанной окружностей треугольника
Формулы для радиусов вписанной и описанной окружностей треугольника Возведение двучлена в любую натуральную степень
Возведение двучлена в любую натуральную степень Роберт Гук
Роберт Гук Деление обыкновенных дробей
Деление обыкновенных дробей Выражение F
Выражение F 6a639551ce27612e
6a639551ce27612e Высшая математика. Глава 1. Элементы линейной алгебры. Лекция 1
Высшая математика. Глава 1. Элементы линейной алгебры. Лекция 1 Окружность и круг
Окружность и круг Решение треугольников
Решение треугольников Приемы решения экономических задач в ЕГЭ
Приемы решения экономических задач в ЕГЭ Таблица сложения
Таблица сложения Тригонометрия. ЕГЭ, задание 7
Тригонометрия. ЕГЭ, задание 7 Чтение дробей
Чтение дробей График функции
График функции Восстановить цепочку вычислений
Восстановить цепочку вычислений Решение систем неравенств
Решение систем неравенств Одночлен. 7 класс
Одночлен. 7 класс Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление
Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление Несобственные интегралы
Несобственные интегралы Задание № 15. Эксперт ЕГЭ
Задание № 15. Эксперт ЕГЭ Сложение и вычитание с переходом через десяток в пределах 10. Интерактивная игра-тренажер по математике Смешарики
Сложение и вычитание с переходом через десяток в пределах 10. Интерактивная игра-тренажер по математике Смешарики подготовка к входной кр 07.09.2022
подготовка к входной кр 07.09.2022 Тела вращения
Тела вращения Системы линейных уравнений. Метод Гаусса
Системы линейных уравнений. Метод Гаусса Понятие. Отношения между понятиями
Понятие. Отношения между понятиями