Содержание
- 2. 1. Задача 1 Два основных метода построения асимптотик: 1) метод итераций 2) метод асимптотических разложений
- 3. 2. Итерации Ocновной шаг метода – такая переформулировка исходной задачи, которая будет базисом итерационного процесса Итерационный
- 4. 3. Асимптотическое разложение Полагаем и находим невозмущенные корни Ищем разложение вблизи в виде ряда по степеням
- 5. 4. Важный момент Когда мы приравниваем коэффициенты при различных степенях к нулю, мы на самом деле
- 6. Ищем разложение в виде ряда по степеням Подставляем разложение в исходное уравнение Сравниваем коэффициенты при различных
- 7. 6. Задача 2: сингулярность У квадратного уравнения два корня. Куда делся второй? Он убежал на бесконечность.
- 8. 7. Задача 2: балансы в уравнении Вычисляя , мы по существу заявили, что главными членами в
- 9. Ищем разложение в виде ряда по степеням Подставляем разложение в исходное уравнение Сравниваем коэффициенты при различных
- 10. 9. Важные моменты Стандартная процедура начинается с нахождения доминирующих членов, определяющих баланс в уравнении. После того
- 11. 10. Еще раз о перенормировках Как найти все полезные перенормировки? Найти все возможные балансы! б) дает
- 12. 11. Задача 3: Нецелые степени ? Причина трудности: Надо было раскладывать по дробным степеням
- 13. 12. Задача 3: Правильное ФАР
- 14. 13. Задача 3: Поиск верного ФАР то Невозможно т.к. то то Невозможно т.к.
- 15. 14. Важный момент В ряде случаев структура ФАР не может задаваться заранее, но должна определяться в
- 16. 15. Итерации: задача 2 Переформулировка Итерационный процесс и начальное приближение 1-я итерация 2-я итерация Переформулировка Итерационный
- 17. 16. Итерации: задача 3 1-я итерация 2-я итерация Переформулировка
- 18. 17. Итерации: почему это работает? - исходное уравнение Итерации будут уменьшать ошибку при Задача 3 -
- 20. Скачать презентацию

















 urok TViMS NSV
urok TViMS NSV Проект по математике. Цифра 5. 1 класс
Проект по математике. Цифра 5. 1 класс Презентация на тему Математика 3 класс Виды треугольников
Презентация на тему Математика 3 класс Виды треугольников  Логарифм числа. Свойства логарифмов
Логарифм числа. Свойства логарифмов Решение задач
Решение задач Диаметр линии второго порядка
Диаметр линии второго порядка Функции
Функции Применение инверсии при построении графиков
Применение инверсии при построении графиков Информатика. Вероятность
Информатика. Вероятность Преемственность в формировании УПК младших школьников и учащихся 5-6 классов на уроках математики посредством интеграции
Преемственность в формировании УПК младших школьников и учащихся 5-6 классов на уроках математики посредством интеграции Несобственные интегралы второго рода
Несобственные интегралы второго рода Методика изучения площади
Методика изучения площади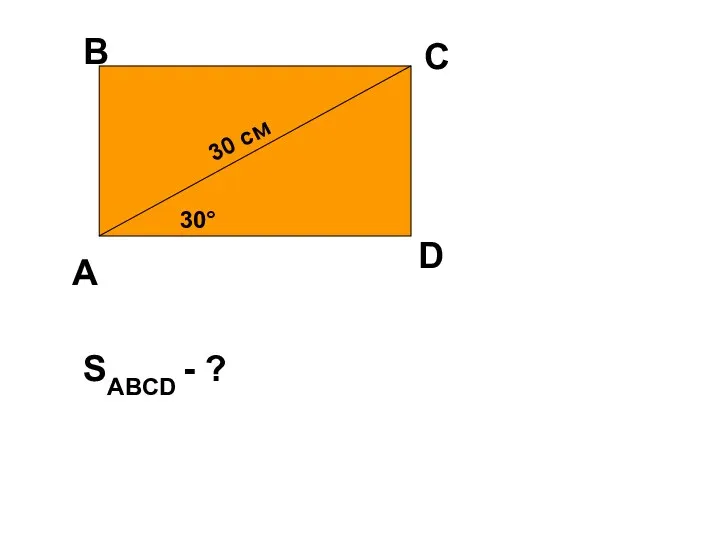 Параметры четырехугольника
Параметры четырехугольника Векторы
Векторы Применение производной к исследованию функции
Применение производной к исследованию функции Задания на развитие логики
Задания на развитие логики Элементы комбинаторики
Элементы комбинаторики Геометрический конструктор: Развивающая игра Танграм
Геометрический конструктор: Развивающая игра Танграм Интеграл, интеграция, интегрирование. Решение задач
Интеграл, интеграция, интегрирование. Решение задач Конус. Решение задач по готовым чертежам
Конус. Решение задач по готовым чертежам Урок – творческий проект по математике Мастерская игрушек
Урок – творческий проект по математике Мастерская игрушек Контрольная работа. Геометрия
Контрольная работа. Геометрия Треугольники. Геометрия, 7 класс
Треугольники. Геометрия, 7 класс Закрепление знания изученных таблиц сложения и вычитания
Закрепление знания изученных таблиц сложения и вычитания окружность — повторение
окружность — повторение Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе
Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе Отрицательные числа
Отрицательные числа Как может математика помочь быть здоровым?
Как может математика помочь быть здоровым?