полукруга по диаметру AB, а каждый полукруг – на одно и то же число равных секторов. Прорези между секторами делают не до конца, чтобы они расходились друг от друга, но не распадались совсем. Секторы одного из полукругов закрашивают. Полукруги ACB и ADB «распрямляют» (насколько это возможно) и закрашенные секторы вставляют между белыми. Получают фигуру близкую по форме к параллелограмму. При достаточно большом числе разбиений на секторы можно с незначительной погрешностью считать высоту получившейся фигуры равной радиусу исходного круга, а длину её основания – равной длине полуокружности.
1 1
2 2
3 3
4 4
5 5
6 6
4
4
3
3
2
2
5
1
1
6
5
6
Площадь круга
Таким образом, площадь круга можно вычислить, умножив длину его полуокружности (2πR/2)на радиус R: S= π R2







 Знакомство с линиями чертежа. Наклонная
Знакомство с линиями чертежа. Наклонная Презентация на тему Начальные понятия планиметрии. Прямая и отрезок. Луч и угол
Презентация на тему Начальные понятия планиметрии. Прямая и отрезок. Луч и угол  Прямоугольник, ромб, квадрат. Решение задач
Прямоугольник, ромб, квадрат. Решение задач Задачи на части
Задачи на части Четырехугольники
Четырехугольники Основные методы решения показательных уравнений, 11 класс, подготовка к ЕГЭ
Основные методы решения показательных уравнений, 11 класс, подготовка к ЕГЭ Четырехугольники. Параллелограмм
Четырехугольники. Параллелограмм Графики функций
Графики функций Булевы выражения. Глава 2
Булевы выражения. Глава 2 Устный счет на уроках математики в 9 классе по подготовке к экзаменам в форме ОГЭ
Устный счет на уроках математики в 9 классе по подготовке к экзаменам в форме ОГЭ Нахождение дроби от числа
Нахождение дроби от числа Презентация на тему Решение уравнений графическим способом
Презентация на тему Решение уравнений графическим способом  Построение графика функции
Построение графика функции Тригонометрия. Математика с Д.А. Власовым
Тригонометрия. Математика с Д.А. Власовым Веселая математика
Веселая математика Образец решения уравнения х2=а
Образец решения уравнения х2=а Квадратная решетка, координатная плоскость
Квадратная решетка, координатная плоскость Прямоугольник
Прямоугольник Равнобедренный треугольник
Равнобедренный треугольник Предметы геометрической формы. Логические задания
Предметы геометрической формы. Логические задания Симметрия. Виды симметрии
Симметрия. Виды симметрии Треугольники. Основные определения
Треугольники. Основные определения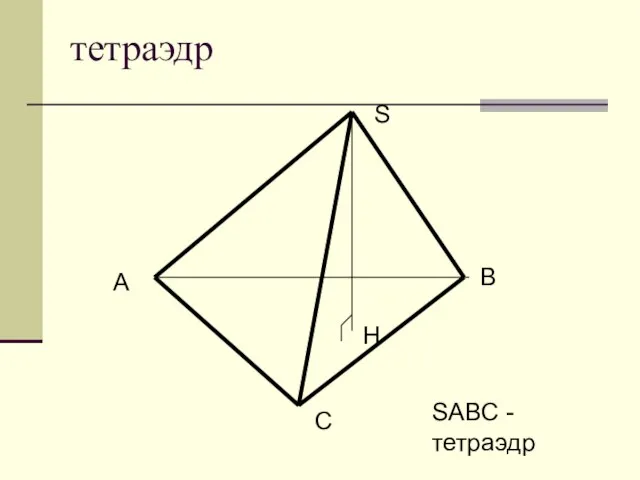 Пирамида. Применение логических законов в решении логических содержательных задач
Пирамида. Применение логических законов в решении логических содержательных задач Арифметические выражения
Арифметические выражения Алгебра событий
Алгебра событий Распределительное свойства умножения
Распределительное свойства умножения Тригонометрические уравнения
Тригонометрические уравнения Деление на 3
Деление на 3