Система нелинейных уравнений (СНУ)

и проверяем условие окончания итерационного процесса
где ε заданная точность
На каждой итерации вычисляем вектор
Решить СНУ с точностью ε=0.1
Преобразуем каждое уравнение

Итерационный процесс расходится.
Попробуем, по другому осуществить преобразование.

Процесс сходится к решению.
2. Общий подход получения эквивалентной системы нелинейных уравнений
Если не удаётся преобразовать исходную СНУ к эквивалентному виду, который будет сходится, то можно воспользоваться общим приемом.
Итерационную формулу запишем
где матрицу
можно представить диагональной, а подбором значений элементов, можно добиться сходимость итерационного процесса.

Метод Ньютона-Рафсона
Пусть известно некоторое приближение
к решению
Запишем исходную систему в виде
где
Разложим функцию в ряд Тейлора и ограничимся линейными членами.
Это система линейных уравнений относительно

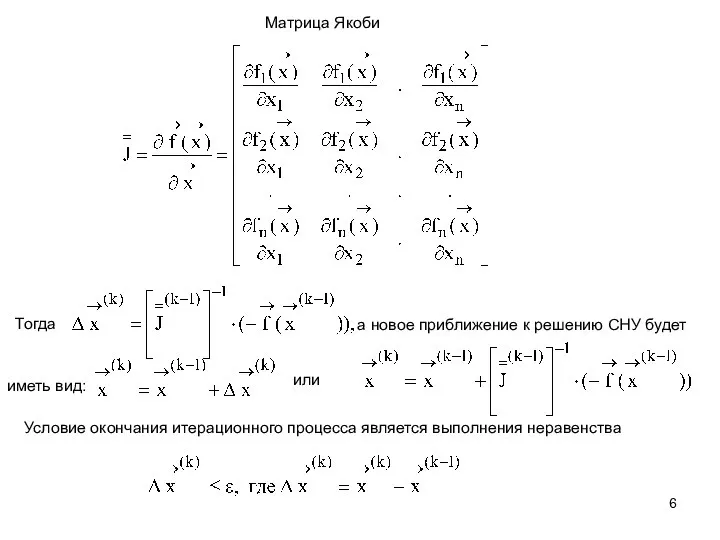
Матрица Якоби
Тогда
иметь вид:
или
а новое приближение к решению СНУ будет
Условие окончания итерационного процесса является выполнения неравенства

Решить приведенный выше пример ε=0.1