Содержание
- 2. Оценки экстремума
- 3. Оценки экстремума т.е. погрешность решения задачи, невозможно. Возможность получения оценок экстремума по конечному числу испытаний зависит
- 4. Оценки экстремума для унимодальных функций Пример. Унимодальная функция на отрезке [0,8].
- 5. Оценки экстремума для унимодальных функций Пусть теперь в общем случае проведено k испытаний в точках и
- 6. Оценки экстремума для липшицевых функций Другим важным классом функций, допускающим построение оценок экстремума по конечному числу
- 7. Рассмотрим одномерную задачу Является ли непрерывная функция липшицевой? Является ли липшицева функция дифференцируемой? Является ли дифференцируемая
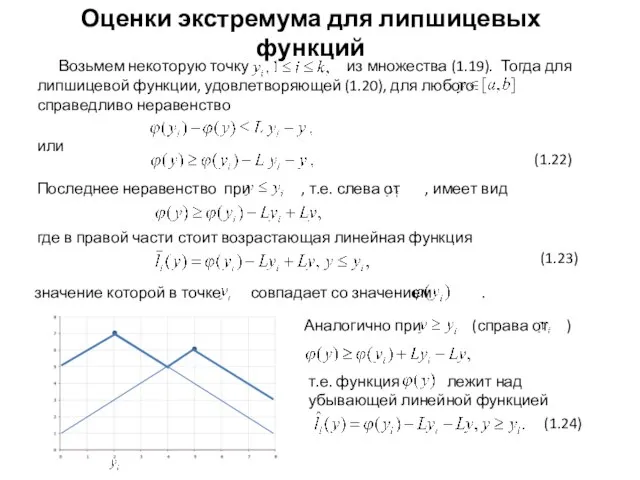
- 8. Возьмем некоторую точку из множества (1.19). Тогда для липшицевой функции, удовлетворяющей (1.20), для любого справедливо неравенство
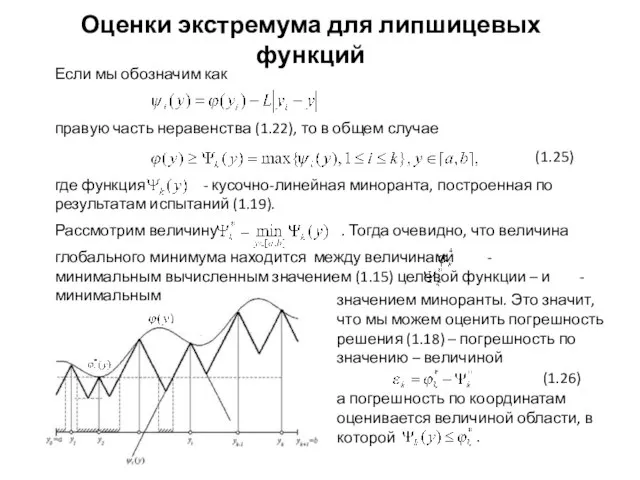
- 9. Если мы обозначим как правую часть неравенства (1.22), то в общем случае значением миноранты. Это значит,
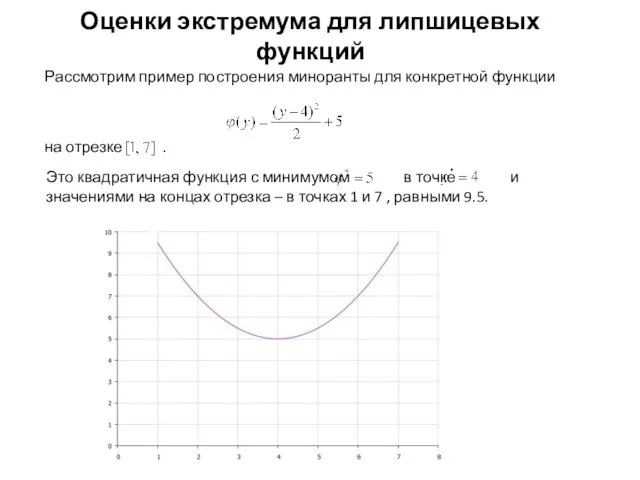
- 10. Оценки экстремума для липшицевых функций Рассмотрим пример построения миноранты для конкретной функции Это квадратичная функция с
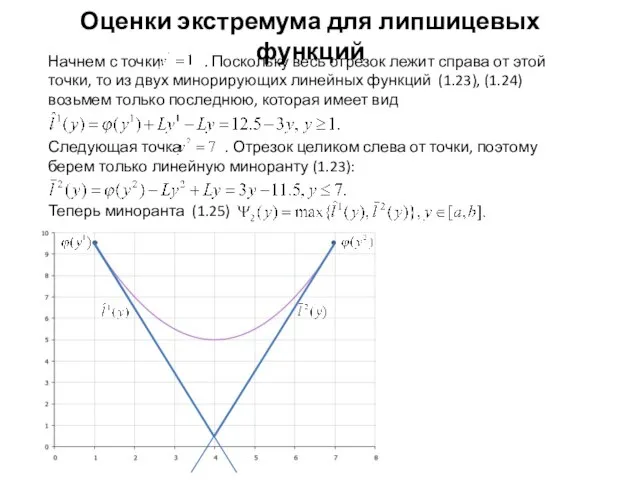
- 11. Оценки экстремума для липшицевых функций Построим последовательно миноранту по 4 точкам:
- 12. Оценки экстремума для липшицевых функций
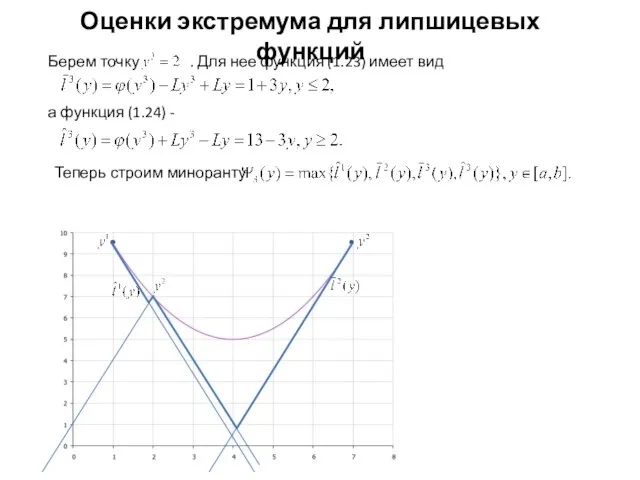
- 13. Оценки экстремума для липшицевых функций Берем точку . Для нее функция (1.23) имеет вид а функция
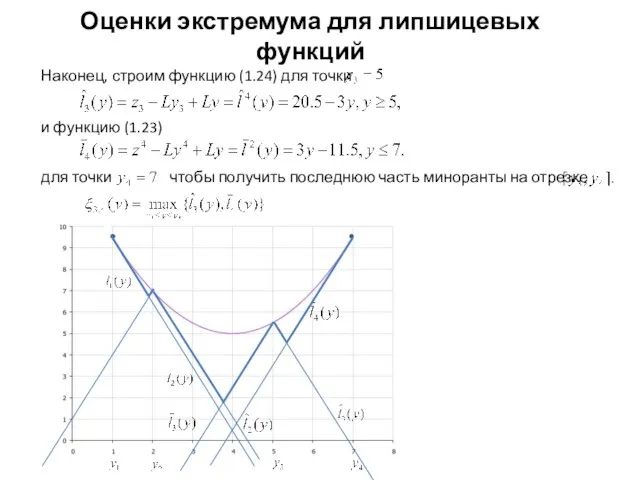
- 14. Оценки экстремума для липшицевых функций а функция (1.24) Конструируем миноранту
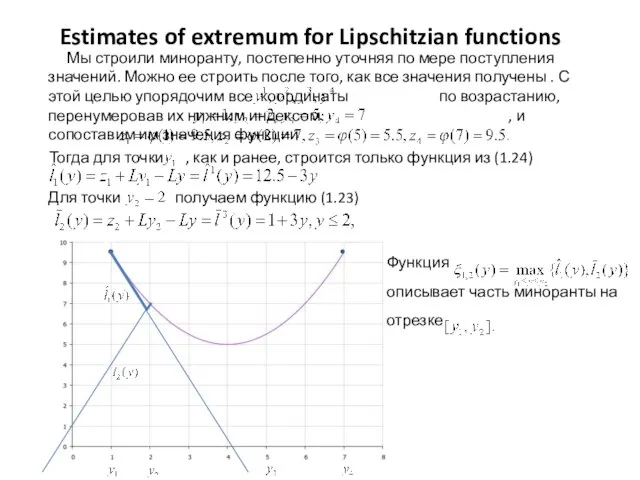
- 15. Estimates of extremum for Lipschitzian functions
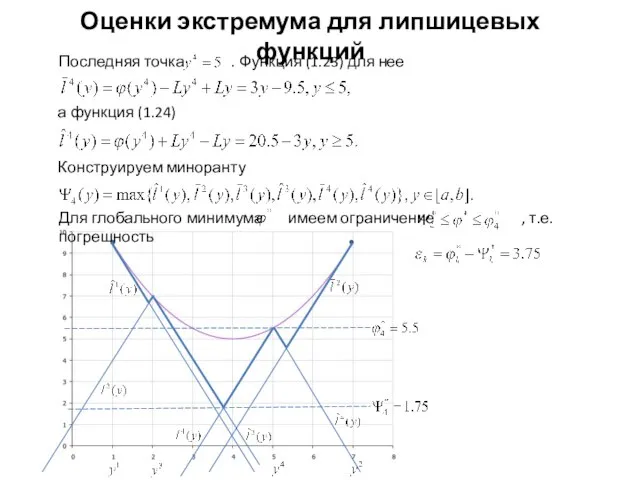
- 16. Оценки экстремума для липшицевых функций
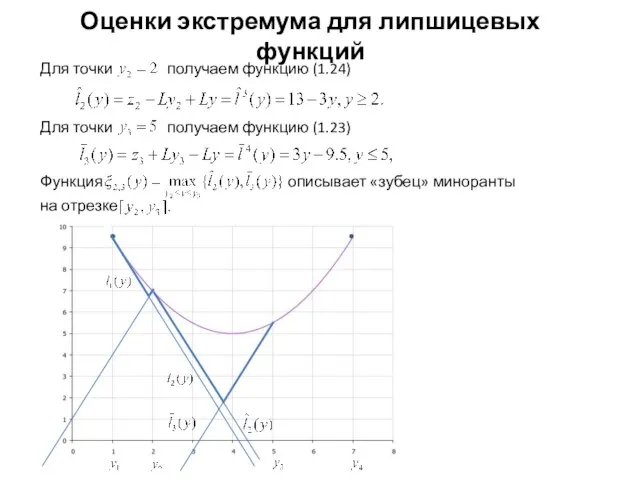
- 17. Оценки экстремума для липшицевых функций и функцию (1.23)
- 18. Оценки экстремума для липшицевых функций где Ее легко найти из равенства откуда
- 20. Скачать презентацию


![Оценки экстремума для унимодальных функций Пример. Унимодальная функция на отрезке [0,8].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/871308/slide-3.jpg)





 Накопленная частота и др
Накопленная частота и др Касательная к окружности. Решение задач
Касательная к окружности. Решение задач Симметрия в пространстве. Понятие правильного многогранника
Симметрия в пространстве. Понятие правильного многогранника Тема_5_2022
Тема_5_2022 Теоретический зачет по теме Начальные геометрические сведения
Теоретический зачет по теме Начальные геометрические сведения Квазистатическое моделирование в системе TALGAT
Квазистатическое моделирование в системе TALGAT Презентация на тему Прямоугольный параллелепипед и его свойства
Презентация на тему Прямоугольный параллелепипед и его свойства  Векторы в пространстве
Векторы в пространстве Выпуклость и вогнутость, точки перегиба графика функции. Лекция 12
Выпуклость и вогнутость, точки перегиба графика функции. Лекция 12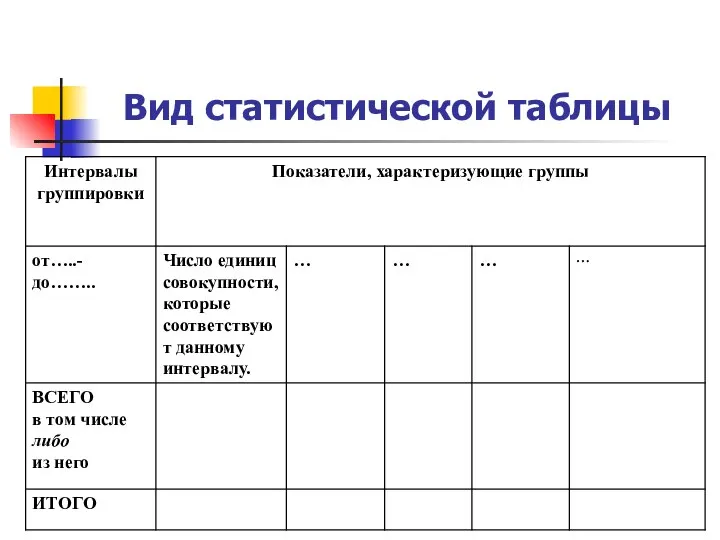 Вид статистической таблицы
Вид статистической таблицы Классическое и статистическое определение вероятности. Основные теоремы теории вероятностей. Лекция 2
Классическое и статистическое определение вероятности. Основные теоремы теории вероятностей. Лекция 2 Скалярное произведение векторов. 9 класс
Скалярное произведение векторов. 9 класс Решение типовой задачи
Решение типовой задачи ПРОЕКТ: Реализация требований ФГОС ООО при обучении учащихся 6 класса теме «Сложение и вычитание рациональных чисел»
ПРОЕКТ: Реализация требований ФГОС ООО при обучении учащихся 6 класса теме «Сложение и вычитание рациональных чисел» Восстанови ряд чисел
Восстанови ряд чисел Игра Музыкальная математика
Игра Музыкальная математика Показательное неравенство
Показательное неравенство Решение задач с помощью уравнений
Решение задач с помощью уравнений Геометрическая прогрессия. Формула n-го члена геометрической прогрессии
Геометрическая прогрессия. Формула n-го члена геометрической прогрессии Сложение и вычитание. Закрепление. Урок математики, 1 класс
Сложение и вычитание. Закрепление. Урок математики, 1 класс Разряды чисел
Разряды чисел Умножение десятичной дроби на десятичную дробь
Умножение десятичной дроби на десятичную дробь Пифагор – основоположник современной геометрии
Пифагор – основоположник современной геометрии Разностные методы решения задач математической физики. Построение разностных схем интегро-интерполяционным методом
Разностные методы решения задач математической физики. Построение разностных схем интегро-интерполяционным методом Математические этюды
Математические этюды Мультиколлинеарность
Мультиколлинеарность Дифференциальные уравнения
Дифференциальные уравнения Множества и операции над ними
Множества и операции над ними