Скаляр, вектор, матрица. 2D геометрия

Вектора
Стрелка: длина и направление
ориентированный сегмент в nD пространстве
Смещение
местоположение,
если задан центр

Вектор определяется направлением и…?
величиной (также называют норма или длина),
Вектор м.б. использован для представления чего?
направления, силы…
Что такое единичный вектор?
вектор величиной 1 (измеряется в выбранных единицах)
Что представляет единичный вектор?
направление (tang, внешняя нормаль)
Что есть sV, где s это скаляр?
вектор с направлением V, но норма масштабирована на s
Что есть U+V?
сумма смещений U и V

Описание векторов
Вектор-строка
Вектор-столбец
Переход с транспонированной формой

Сложение вектор-вектор
Сложить: vector + vector = vector
Правило параллелограмма
“хвост к голове” закончит треугольник
геометрически
алгебраически
Примеры:

Вычитание вектор-вектор
вычитание: vector - vector = vector
Примеры:

Умножение Скаляр-вектор
умножение: scalar * vector = vector
Вектор масштабируется
Примеры:

Умножение вектор-вектор
умножение: vector * vector = scalar
скалярное произведение

Умножение вектор-вектор (2)
умножение : vector * vector = scalar
скалярное произведение

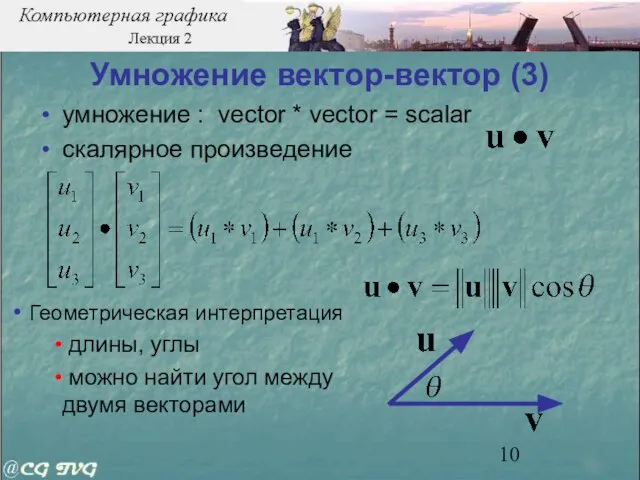
Геометрическая интерпретация
длины, углы
можно найти угол между двумя векторами
Умножение вектор-вектор (3)
умножение : vector * vector = scalar
скалярное произведение

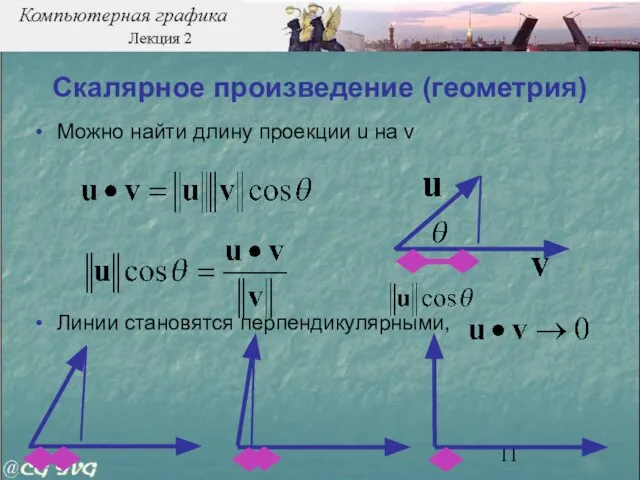
Скалярное произведение (геометрия)
Можно найти длину проекции u на v
Линии становятся перпендикулярными,

Скалярное произведение (2)
U∙V = ||U||⋅||V||⋅cos(angle(U,V)) U∙V - скаляр.
U and V ортогональны ⇒ U∙V==0
U∙V==0 ⇒ ( U==0 или V==0 или (U и V ортогональны)
U∙V положительно если угол между U и V меньше 90o
U∙V = V∙U, потому, что: cos(a)=cos(–a).
u∙v = cos(angle(u,v) # unit vectors: ||u|| = ||v|| = 1
Скалярное произведение двух единичных векторов - косинус их угла
V∙u = длина проекции V в направлении (единич.вектор) u
||U||= √(U∙U) = длина U = норма U
U2 = U∙U (короткая форма для ||U||2)
V∙U = U∙V < 0
V∙U = U∙V > 0

Скалярное произведение(пример)

Что измеряет скалярное произведение V•U когда U единич.вектор?
Спроектированное смещение V на U
Чему равно V•U когда U и V единич.вектора?
cos( angle(U,V) )
Чему равно V•U для обычных U и V?
cos( angle(U,V) ) V.norm U.norm
Когда V•U=0?
U.norm=0 OR V.norm=0 OR U и V ортогональны
Когда V•U>0?
если угол между U и V меньше 90o
Как подсчитать V•U?
U.xV.x+U.yV.y
Что такое V2?
V2 = V•V = (V.norm)2

умножение: vector * vector = vector
перекрестное произведение
алгебраически
Скалярное произведение(Продолжение)

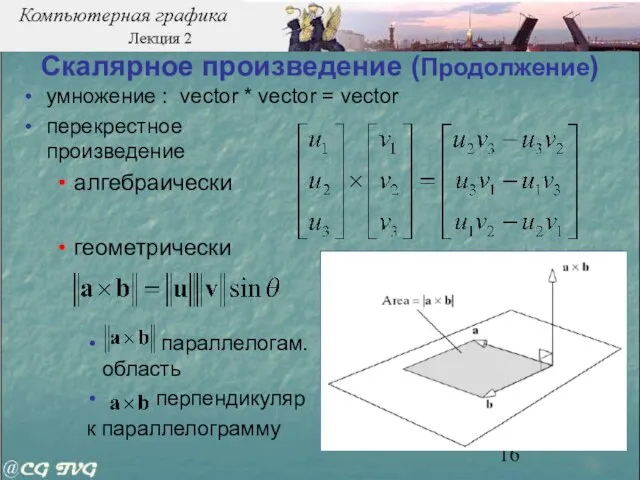
умножение : vector * vector = vector
перекрестное
произведение
алгебраически
геометрически
параллелогам.
область
перпендикуляр
к параллелограмму
Скалярное произведение (Продолжение)

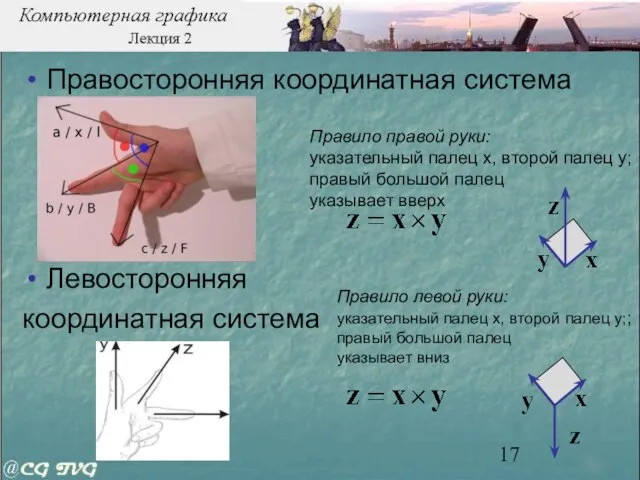
Правосторонняя координатная система
Левосторонняя
координатная система
Правило правой руки:
указательный палец x, второй палец y;
правый большой палец
указывает вверх
Правило левой руки:
указательный палец x, второй палец y;;
правый большой палец
указывает вниз

Векторы базиса
Взять любых два линейно-независимых вектора (не равных 0 и не ||)
Можно использовать их линейную комбинацию для определения
любого другого
вектора :

Ортонормальный базисный вектор
Если базисные вектора ортонормальные
( ортонормальные( перпендикулярные) и единичной длины)
Мы имеем Картезианскую (Декартову) систему координат
знакомое Пифагорово
определение расстояния
Ортонормальные алгебраические свойства

Стандартные единичные векторы в 3D
i = (1,0,0)
j = (0,1,0)
k = (0,0,1)
Правая рука Левая рука

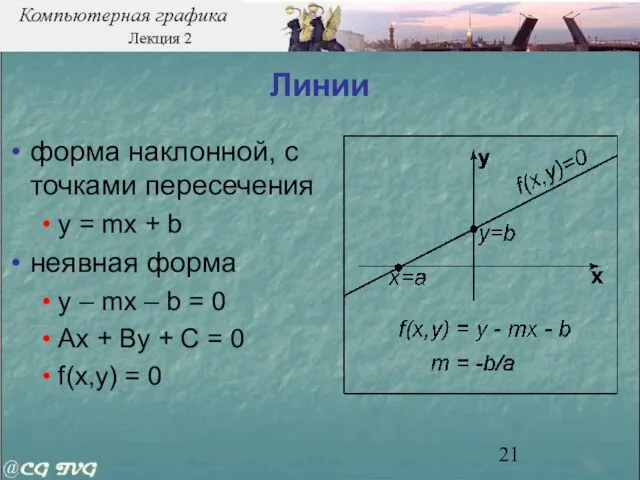
Линии
форма наклонной, с
точками пересечения
y = mx + b
неявная форма
y – mx – b = 0
Ax + By + C = 0
f(x,y) = 0

Окружность
окружность – это точки (x,y), где f(x,y) = 0
точки p на окружности имеют свойство, что вектор из c в p дает скалярное произведение r2
точки p на окружности имеют свойство, что квадрат расстояния из c в p - r2
точки p на окружности – расстоние r из центра c

Параметрические кривые
Параметр: индекс изменяющийся непрерывно
(x,y): точка на кривой
t: параметр
Вектор из

2D параметрическая линия
Начинается в точке p0,
и идет до p1,
в соответствии с параметром t
p(0) = p0, p(1) = p1

Линейная интерполяция
Параметричекая линия пример следующих общих поняти1
интерполяция
p идет через a в t = 0
p идет через b в t = 1
линейность
веса t, (1-t) линейные полиномиалы в t

Матрицы
Множество чисел (m×n = m строки, n столбцы)
Сложение, умножение скаляром просто : элемент за элементом

Сложение матриц
сложение: matrix + matrix = matrix
пример

Умножение скаляр - матрица
умножение: скаляр * matrix = matrix
пример

Умножение матрица-матрица
Можно только умножить (n,k) на (k,m):
число левых столбцов = числу правых строк
разрешено
неопределено

Строка на столбец
Умножение матрица-матрица

Строка на столбец
Умножение матрица-матрица

Строка на столбец
Умножение матрица-матрица

Строка на столбец
Умножение матрица-матрица

Строка на столбец
некоммутативно: AB != BA
Умножение матрица-матрица

точки вектора-столбца: постумножаются
точки вектора-строка : предумножаются
Умножение матрица-вектор

Пример умножения матриц
Умножение матрица-матрица

транспонированная
идентичности
обратная
не все матрицы являются обратимыми
Матрицы

Пространства
Точка в - положение этой точки.
Для описания положения точки можно использовать:
- Векторное (линейное) пространство
- Аффинное пространство
- Евклидово пространство

Линейное пространство создают скаляры и векторы.
Аффинное пространство – добавляется понятие точки.
Евклидово пространство – вводят понятие расстояние.
Системы координат: Положение точки в пространстве может быть описано в виде комбинации некоторых линейно-независимых векторов .
Если ввести скаляры , то можно описать вектор (положение точки) так:

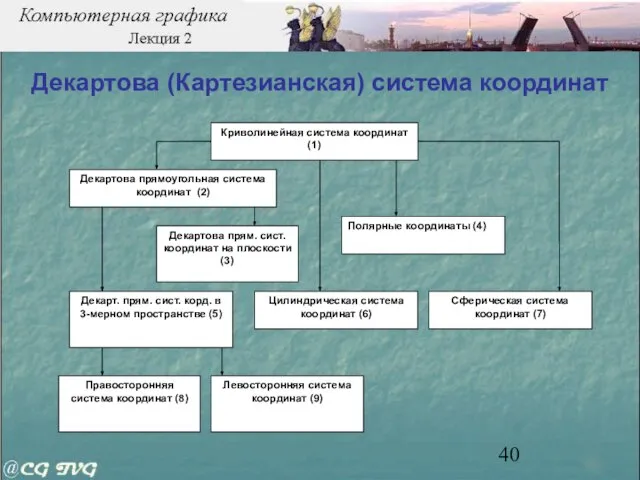
Декартова (Картезианская) система координат

Базовая косоугольная система координат
Координаты определяются осями ( х – ось абсцисс, у - ось ординат)
Расстояние определяется проекциями
Полярная система координат
Точка О – полюс, - полярный угол , r – полярное расстояние.

Цилиндрические координаты