Содержание
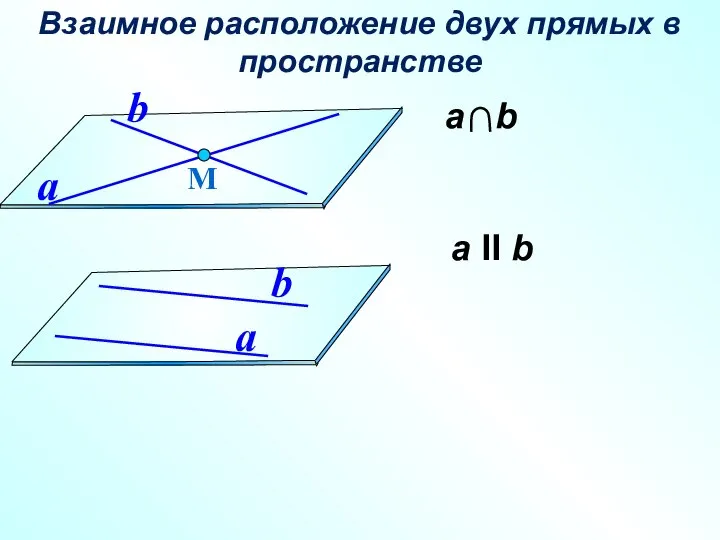
- 2. а II b Взаимное расположение двух прямых в пространстве М a b a b
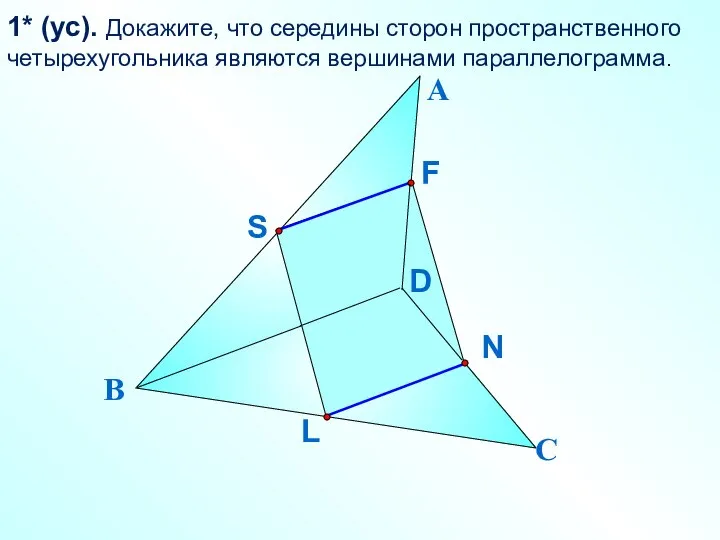
- 3. 1* (ус). Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма. А В С D
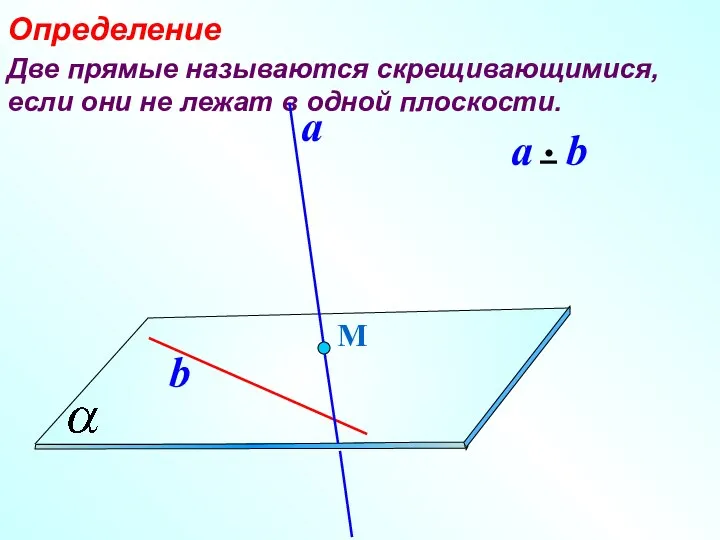
- 4. Две прямые называются скрещивающимися, если они не лежат в одной плоскости. Определение М a b
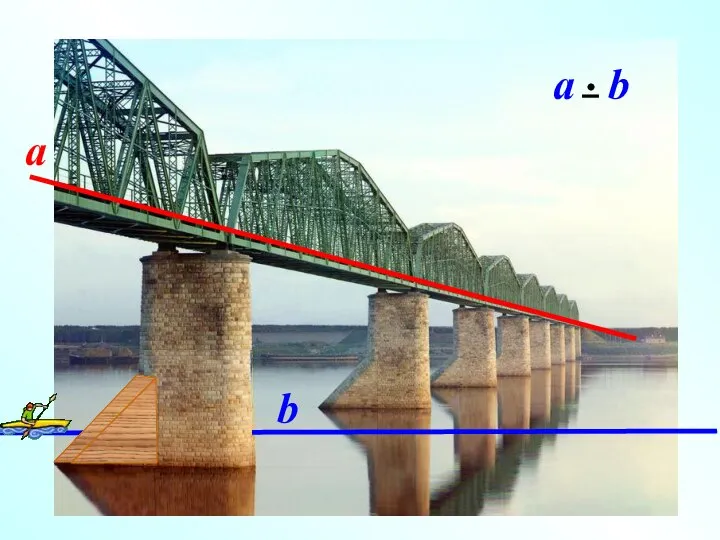
- 5. IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIi Наглядное представление о скрещивающихся прямых дают две дороги, одна из которых проходит по эстакаде, а
- 6. a b
- 7. Найдите на рисунке параллельные прямые. Назовите параллельные прямые и плоскости. Найдите скрещивающиеся прямые
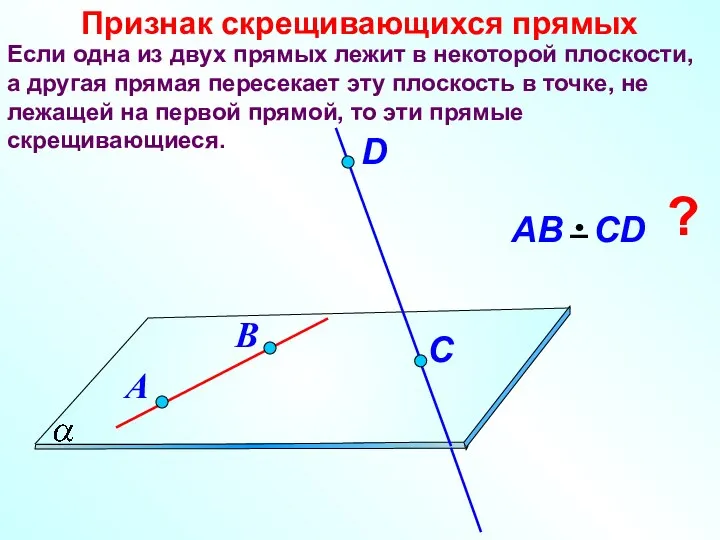
- 8. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в
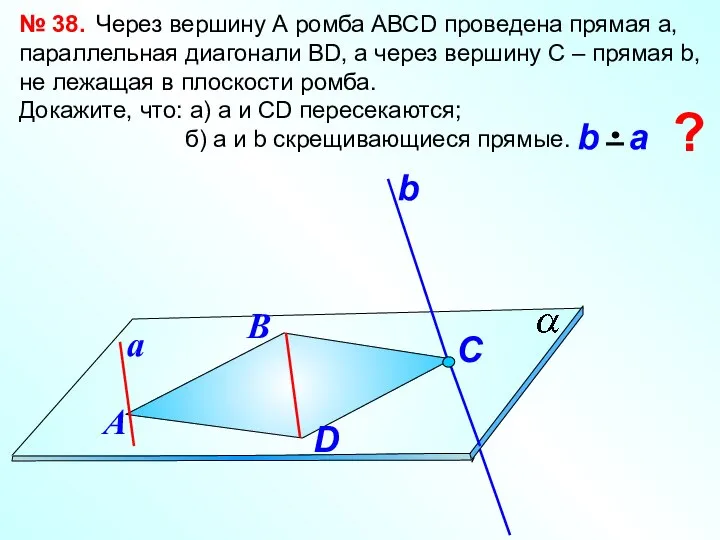
- 9. № 38. Через вершину А ромба АВСD проведена прямая а, параллельная диагонали ВD, а через вершину
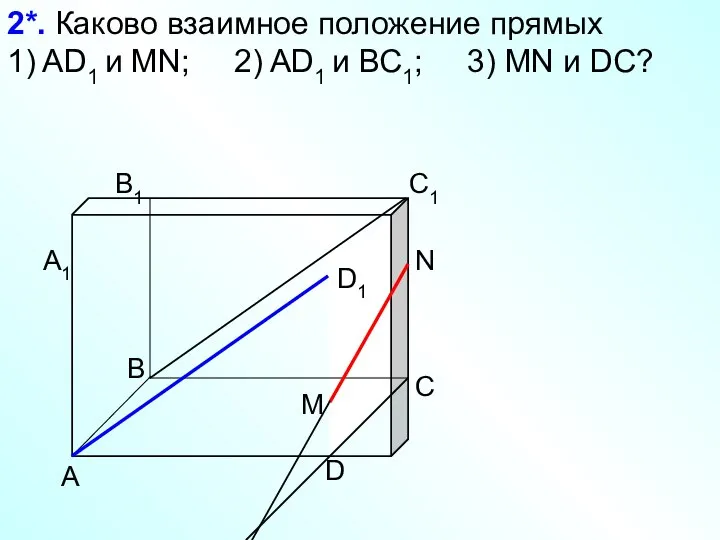
- 10. А D С В B1 С1 D1 А1 2*. Каково взаимное положение прямых 1) AD1 и
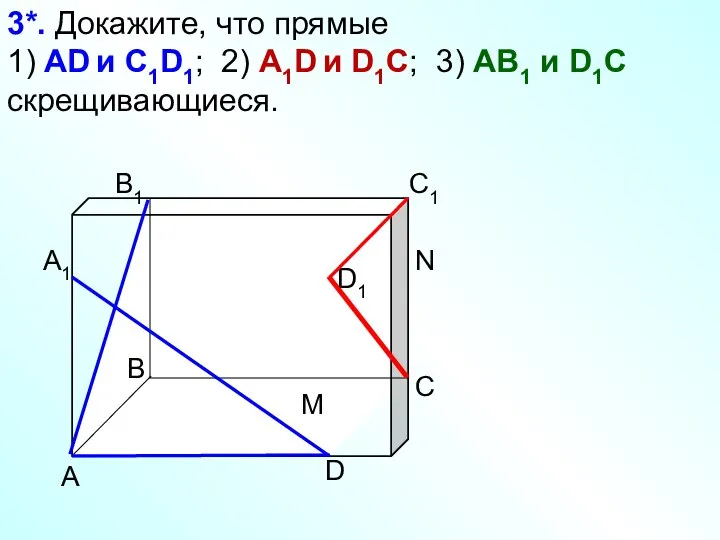
- 11. А D С В B1 С1 D1 А1 3*. Докажите, что прямые 1) AD и C1D1;
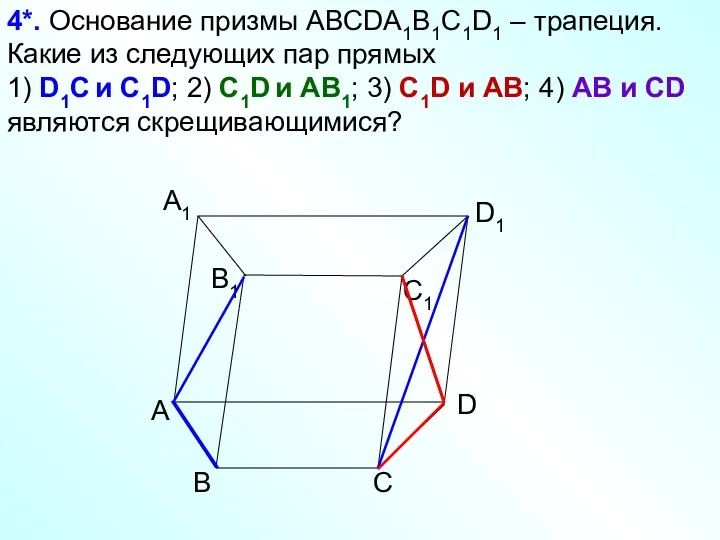
- 12. А D С В B1 С1 D1 А1 4*. Основание призмы АВСDA1B1C1D1 – трапеция. Какие из
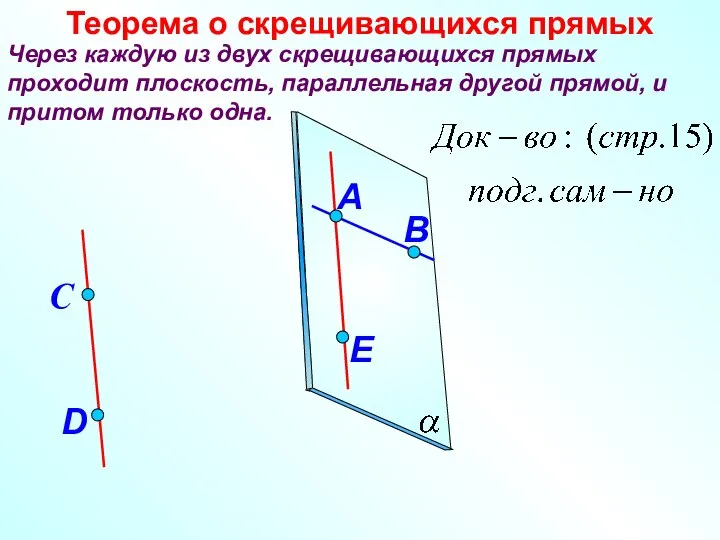
- 13. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна. Теорема
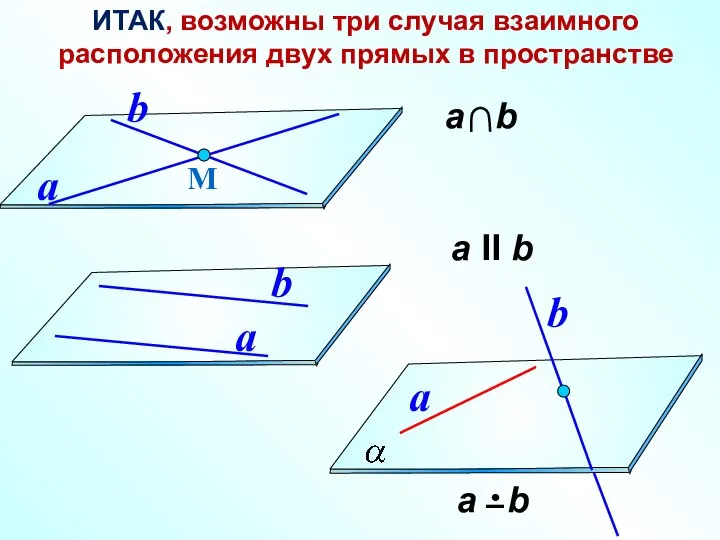
- 14. а II b ИТАК, возможны три случая взаимного расположения двух прямых в пространстве М a b
- 16. Скачать презентацию


 Прямоугольник
Прямоугольник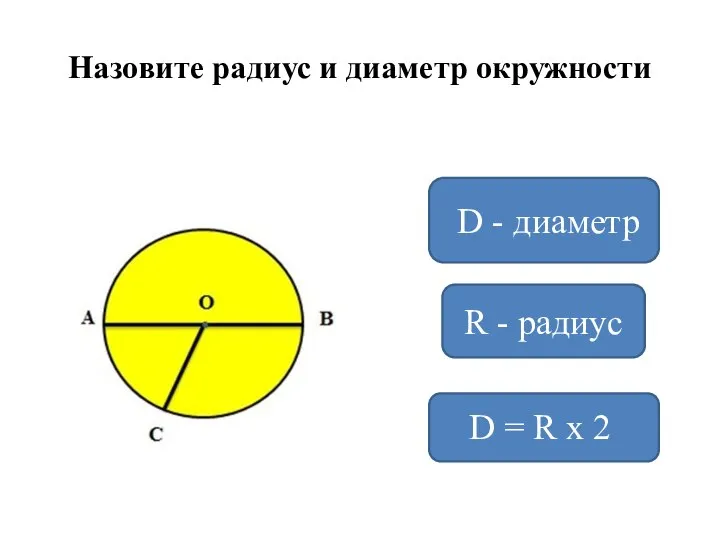 Радиус и диаметр окружности
Радиус и диаметр окружности Сочетания. Задачи
Сочетания. Задачи Единицы стоимости. Рубль, копейка
Единицы стоимости. Рубль, копейка Презентация на тему Теорема Пифагора и её применение
Презентация на тему Теорема Пифагора и её применение  Решение задач на свойства
Решение задач на свойства Приемы письменных вычислений в пределах 1000. 3 класс
Приемы письменных вычислений в пределах 1000. 3 класс Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1
Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1 Нахождение синуса острого угла в прямоугольном треугольнике
Нахождение синуса острого угла в прямоугольном треугольнике Сложение векторов. Сложение сил
Сложение векторов. Сложение сил Обыкновенные дроби. Задания для устного счета. 8 класс
Обыкновенные дроби. Задания для устного счета. 8 класс Презентация на тему Круг. Площадь круга
Презентация на тему Круг. Площадь круга  Вправи на засвоєння таблиці додавання і віднімання числа 7
Вправи на засвоєння таблиці додавання і віднімання числа 7 История развития обыкновенных дробей
История развития обыкновенных дробей Приемы сложения и вычитания в пределах 20 с переходом через десяток
Приемы сложения и вычитания в пределах 20 с переходом через десяток Вывод формулы длины окружности и площади круга
Вывод формулы длины окружности и площади круга Углы с сонаправленными сторонами
Углы с сонаправленными сторонами Степінь з цілим показником
Степінь з цілим показником Решение планиметрических задач
Решение планиметрических задач Презентация на тему Противоположные числа (6 класс)
Презентация на тему Противоположные числа (6 класс)  Сложные проценты. Контрольная
Сложные проценты. Контрольная Презентация на тему Таблицы истинности
Презентация на тему Таблицы истинности  Задачи на движение
Задачи на движение Уравнение окружности
Уравнение окружности Скалярное произведение векторов
Скалярное произведение векторов Калейдоскоп заданий ОГЭ. Математическая игра
Калейдоскоп заданий ОГЭ. Математическая игра Презентация на тему Сочетательное свойство сложения
Презентация на тему Сочетательное свойство сложения  Объемы многогранников
Объемы многогранников