и только одно возможное значение, наперёд не известное и зависящее от случайных обстоятельств, которые заранее не могут быть учтены.
Пример. Выпадение определённого числа очков на игральной кости (от 1 до 6). Число очков – случайная величина.
Дискретная случайная величина – случайная величина, которая может принимать конечные, изолированные значения из некоторого числового промежутка
Непрерывная случайная величина – случайная величина, которая может принимать все значения из некоторого числового промежутка
Пример. Содержание какого-либо фермента в крови
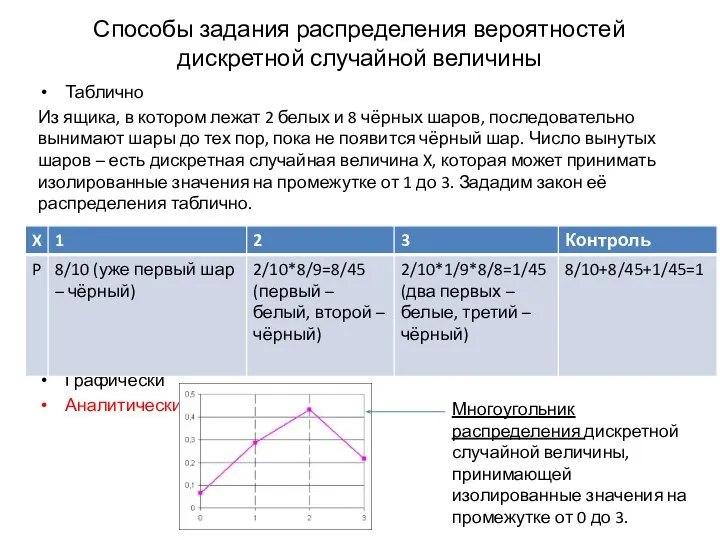
Закон распределения вероятностей дискретной случайной величины – это сопоставление всех возможных значений случайной величины и их вероятностей.
Тривиальный пример. Случайная величина – сторона монетки. Она принимает два изолированных значения – либо «орёл», либо «решка» и подчинена следующему закону распределения:
Название случайной величины
Вектор вероятностей







 Алан Тьюринг
Алан Тьюринг Урок математики в 1 классе
Урок математики в 1 классе Алгоритм задачи
Алгоритм задачи Нелинейная парная регрессия
Нелинейная парная регрессия Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного
Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного Теория вероятностей
Теория вероятностей Логарифмические уравнения
Логарифмические уравнения Многочлены над числовыми полями
Многочлены над числовыми полями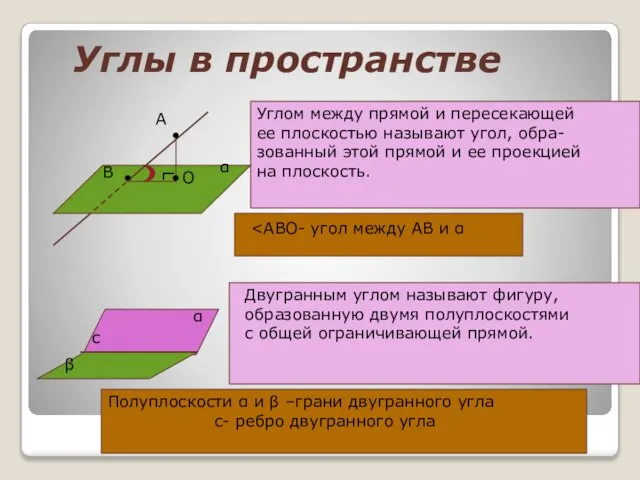 Двугранный угол. Угол между плоскостями. Перпендикулярность двух плоскостей
Двугранный угол. Угол между плоскостями. Перпендикулярность двух плоскостей Действия со смешанными числами
Действия со смешанными числами Сравнение чисел
Сравнение чисел Математика и режим дня
Математика и режим дня Тесты по математике
Тесты по математике Вставьте пропущенные числа
Вставьте пропущенные числа Презентация на тему Угол. Прямой и развернутый угол
Презентация на тему Угол. Прямой и развернутый угол  Приёмы решения показательных уравнений
Приёмы решения показательных уравнений Повторение курса алгебры за 10 класс
Повторение курса алгебры за 10 класс Математика-2
Математика-2 9
9 Уравнение с двумя переменными
Уравнение с двумя переменными Показательные уравнения
Показательные уравнения Построение аксонометрических проекций геометрических фигур и тел
Построение аксонометрических проекций геометрических фигур и тел Задание В11, открытого банка ЕГЭ по математике (часть 1)
Задание В11, открытого банка ЕГЭ по математике (часть 1) Сопоставимость показателей. Лекция 2
Сопоставимость показателей. Лекция 2 Решение уравнений в целых числах
Решение уравнений в целых числах Примеры. Математика
Примеры. Математика Обыкновенные дроби. Эти таежные животные
Обыкновенные дроби. Эти таежные животные Решение неравенств (найди ошибку)
Решение неравенств (найди ошибку)