Содержание
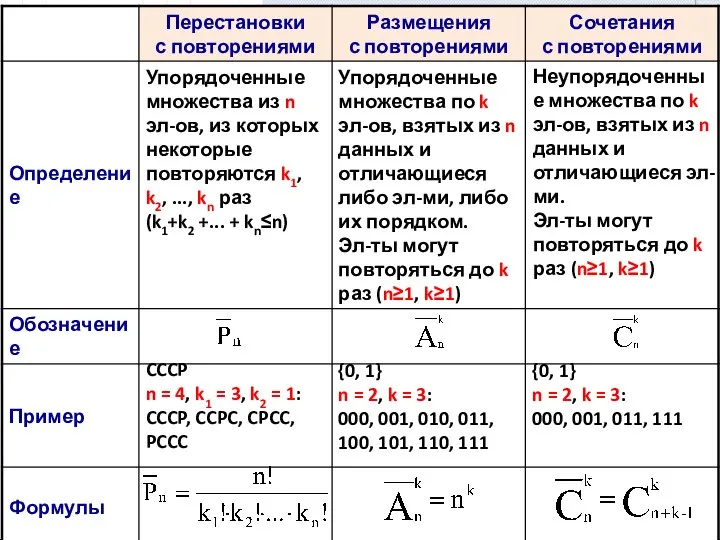
- 2. Упорядоченные множества из n эл-ов, из которых некоторые повторяются k1, k2, ..., kn раз (k1+k2 +...
- 3. Задача №1. Сколько различных «слов» можно составить из слова «ЛАОКООН», если каждое «слово» содержит семь букв,
- 4. Задача №2. Сколько разных «слов» из четырех букв можно составить из слова «мама»? Дано: U =
- 5. Задача №3. Сколько «слов» по две буквы можно составить из трех букв: F, T, C? Дано:
- 6. Задача №4. Сколько «слов» по три буквы можно составить из двух букв E и N? Дано:
- 7. Задача №5. В школьной столовой на десерт дают яблоки и груши. В комплект входит три плода
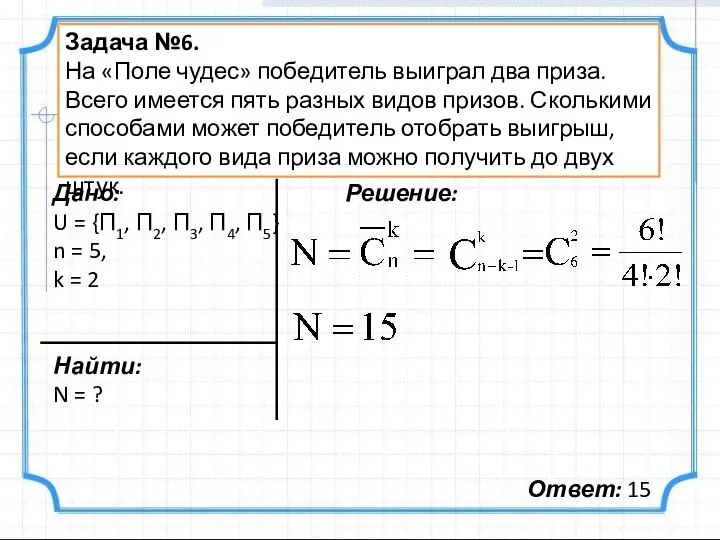
- 8. Задача №6. На «Поле чудес» победитель выиграл два приза. Всего имеется пять разных видов призов. Сколькими
- 10. Скачать презентацию





 Зимующие птицы. Дети 5 лет
Зимующие птицы. Дети 5 лет Деление обыкновенных дробей
Деление обыкновенных дробей С математикой в космос
С математикой в космос Вариационная форма
Вариационная форма Презентация на тему Формулы
Презентация на тему Формулы  Многоугольники в нашей жизни
Многоугольники в нашей жизни Объем конуса и цилиндра
Объем конуса и цилиндра График функции
График функции Объём прямой призмы
Объём прямой призмы Увлекательный мир умножения
Увлекательный мир умножения Пропорции. Решение уравнений
Пропорции. Решение уравнений Презентация на тему Медицина и математика
Презентация на тему Медицина и математика  Действительные числа
Действительные числа Математика. Дополнительные задачи
Математика. Дополнительные задачи Устный счет на уроках математики в 9 классе по подготовке к экзаменам в форме ОГЭ
Устный счет на уроках математики в 9 классе по подготовке к экзаменам в форме ОГЭ Презентация на тему Окружность. Круг.
Презентация на тему Окружность. Круг.  Решение задач на дроби. 6 класс
Решение задач на дроби. 6 класс Урок по учебнику Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков Алгебра 9 с углубленным изучением математики
Урок по учебнику Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков Алгебра 9 с углубленным изучением математики Масштаб чертежа
Масштаб чертежа Riešenie rovníc, ak je neznáma na oboch stranách rovnice
Riešenie rovníc, ak je neznáma na oboch stranách rovnice Презентация на тему ДЕЛИТЕЛИ И КРАТНЫЕ
Презентация на тему ДЕЛИТЕЛИ И КРАТНЫЕ  Презентация на тему Единица времени – сутки (4 класс)
Презентация на тему Единица времени – сутки (4 класс)  Задачи на готовом чертеже. 9 класс
Задачи на готовом чертеже. 9 класс Цилиндр. Цилиндры вокруг нас
Цилиндр. Цилиндры вокруг нас Функции многих переменных
Функции многих переменных Презентация на тему Математический диктант
Презентация на тему Математический диктант 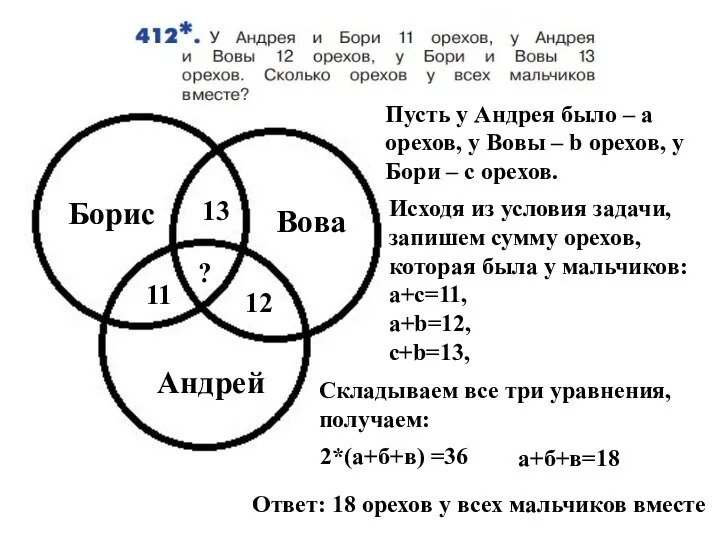 Уравнения. Задача
Уравнения. Задача Презентация на тему Решение задач - Треугольники
Презентация на тему Решение задач - Треугольники