Содержание
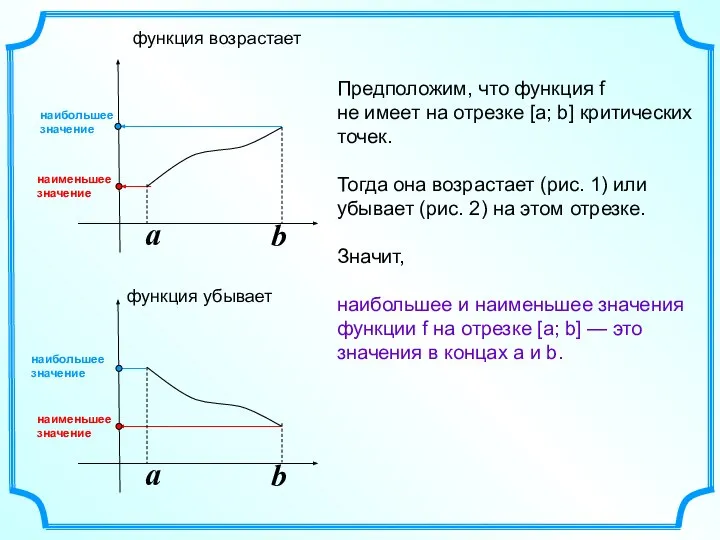
- 2. a b a b Предположим, что функция f не имеет на отрезке [а; b] критических точек.
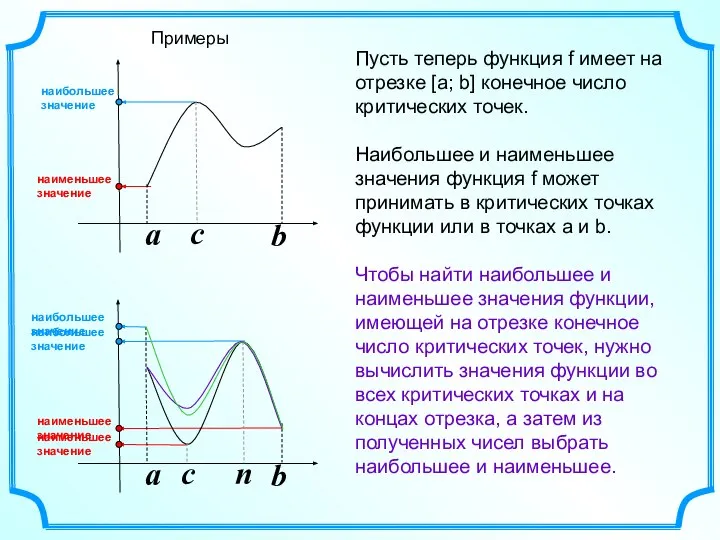
- 3. a b a b Пусть теперь функция f имеет на отрезке [а; b] конечное число критических
- 4. Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4] 1. Найдем критические
- 5. Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4] 1) y /
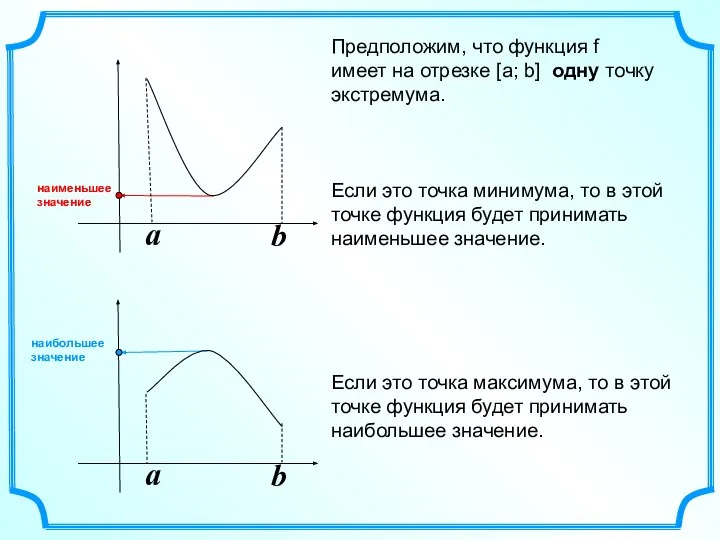
- 6. a b a b Предположим, что функция f имеет на отрезке [а; b] одну точку экстремума.
- 7. Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4] 1) y /
- 8. Найдем критические точки, которые принадлежат заданному отрезку. Выбрать наибольшее из полученных значений. 1) y(0) = 4
- 9. Найдем критические точки, которые принадлежат заданному отрезку. Выбрать наименьшее из полученных значений. 1) y(1) = 1
- 10. Найдите наибольшее значение функции на отрезке [ -3; 3 ] 4. Найдем критические точки, которые принадлежат
- 11. Найдите наибольшее значение функции на отрезке [ 1; 9 ] 5. Найдем критические точки, которые принадлежат
- 12. Найдите наименьшее значение функции на отрезке [ 1; 9 ] 6. Найдем критические точки, которые принадлежат
- 13. Найдите наименьшее значение функции на отрезке [-10; 1 ] 7. Найдем критические точки, которые принадлежат заданному
- 14. Найдите наименьшее значение функции на отрезке [-10; 1 ] 7. Найдем критические точки, которые принадлежат заданному
- 15. Найдите наибольшее значение функции на отрезке [ 1; 9 ] 8. Найдем критические точки, которые принадлежат
- 16. Найдите наибольшее значение функции на отрезке [ 3; 10 ] 9. Найдем критические точки, которые принадлежат
- 17. Найдите наименьшее значение функции на отрезке [ 1; 7 ] 10. Найдем критические точки, которые принадлежат
- 18. Найдите наибольшее значение функции y = ln(x+5)5 – 5x на отрезке [-4,5; 0] 11. max Наибольшее
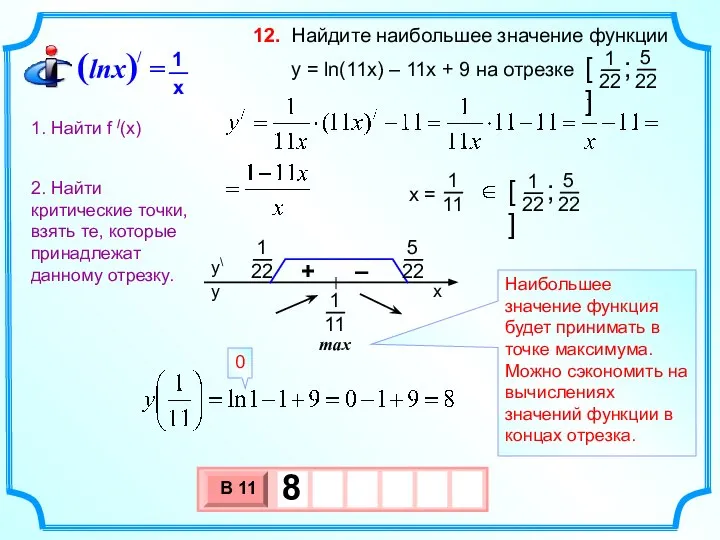
- 19. Найдите наибольшее значение функции y = ln(11x) – 11x + 9 на отрезке 12. max Наибольшее
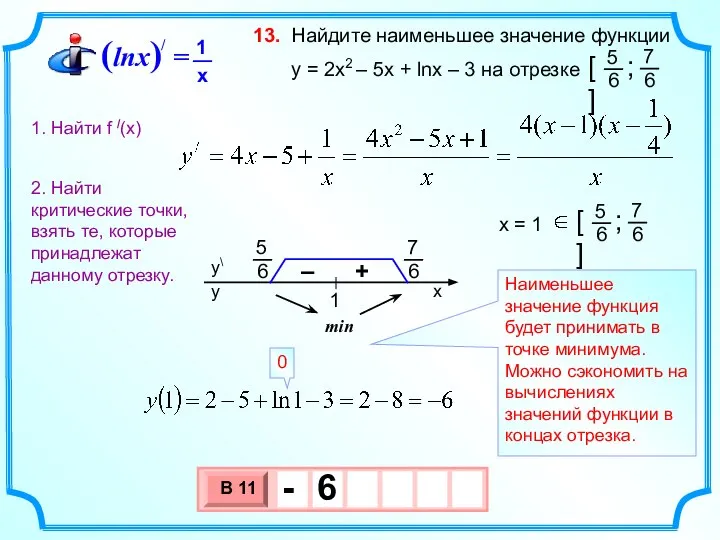
- 20. Найдите наименьшее значение функции y = 2х2 – 5x + lnx – 3 на отрезке 13.
- 21. Найдите наибольшее значение функции y = 7cosx +16x – 2 на отрезке 14. Функция на всей
- 22. Критических точек нет. Тогда наибольшее значение функция будет принимать в одном из концов отрезка. Можно было
- 23. Функция на всей области определения убывает. Нетрудно догадаться, что у / Тогда наименьшее значение функция будет
- 24. Найдите наибольшее значение функции y = 12cosx + 6 x – 2 + 6 на отрезке
- 25. Найдите наибольшее значение функции y = 12cosx + 6 x – 2 + 6 на отрезке
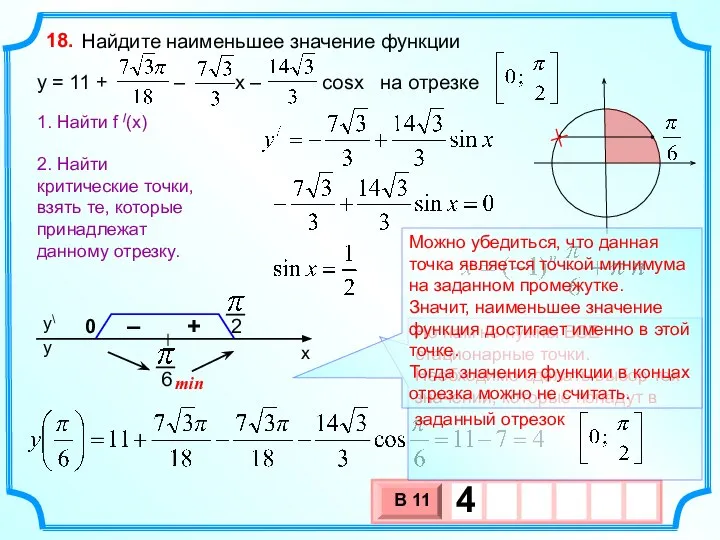
- 26. Найдите наименьшее значение функции y = 11 + – х – cosx на отрезке 18. 1.
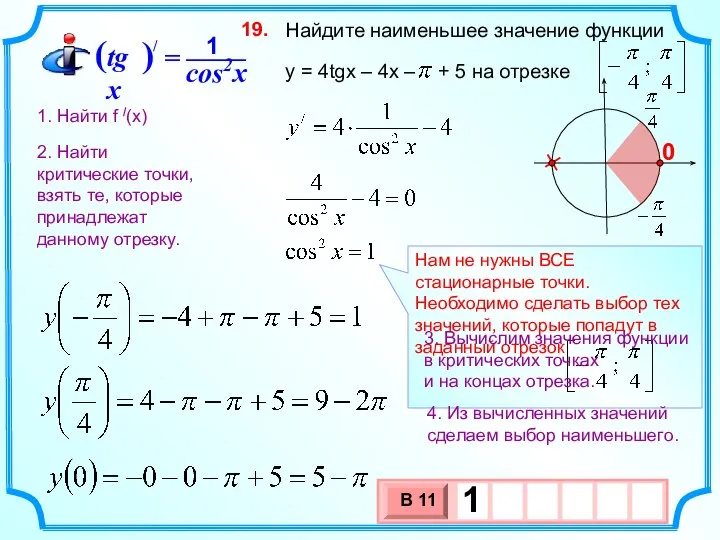
- 27. Найдите наименьшее значение функции y = 4tgx – 4x – + 5 на отрезке 19. 1.
- 28. Найдите наибольшее значение функции y = 3tgx – 3x + 5 на отрезке 20. 1. Найти
- 30. Скачать презентацию





![Найдите наибольшее значение функции на отрезке [ -3; 3 ] 4. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/963711/slide-9.jpg)
![Найдите наибольшее значение функции на отрезке [ 1; 9 ] 5. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/963711/slide-10.jpg)
![Найдите наименьшее значение функции на отрезке [ 1; 9 ] 6. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/963711/slide-11.jpg)
![Найдите наименьшее значение функции на отрезке [-10; 1 ] 7. Найдем критические](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/963711/slide-12.jpg)
![Найдите наименьшее значение функции на отрезке [-10; 1 ] 7. Найдем критические](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/963711/slide-13.jpg)
![Найдите наибольшее значение функции на отрезке [ 1; 9 ] 8. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/963711/slide-14.jpg)
![Найдите наибольшее значение функции на отрезке [ 3; 10 ] 9. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/963711/slide-15.jpg)
![Найдите наименьшее значение функции на отрезке [ 1; 7 ] 10. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/963711/slide-16.jpg)







 Проверка математических данных в произведении Н. Носова Незнайка на Луне
Проверка математических данных в произведении Н. Носова Незнайка на Луне Площадь. Фигуры
Площадь. Фигуры Задание 19. Профиль (1)
Задание 19. Профиль (1) Упрощение выражений. Тест
Упрощение выражений. Тест Формулы сложения
Формулы сложения Движение по окружности
Движение по окружности Вавилонская математика
Вавилонская математика ЛекцияЭлементы комбинаторики
ЛекцияЭлементы комбинаторики Прямая и обратная пропорциональность
Прямая и обратная пропорциональность Презентация4. МСиТИ
Презентация4. МСиТИ Уравнение касательной к графику функции
Уравнение касательной к графику функции Первые уроки в 5 кассе
Первые уроки в 5 кассе Задачи на проценты
Задачи на проценты Числовые равенства и их свойства
Числовые равенства и их свойства Площадь ромба
Площадь ромба Сочетания. 9 класс
Сочетания. 9 класс Двугранный угол
Двугранный угол Золотое сечение. 9 класс
Золотое сечение. 9 класс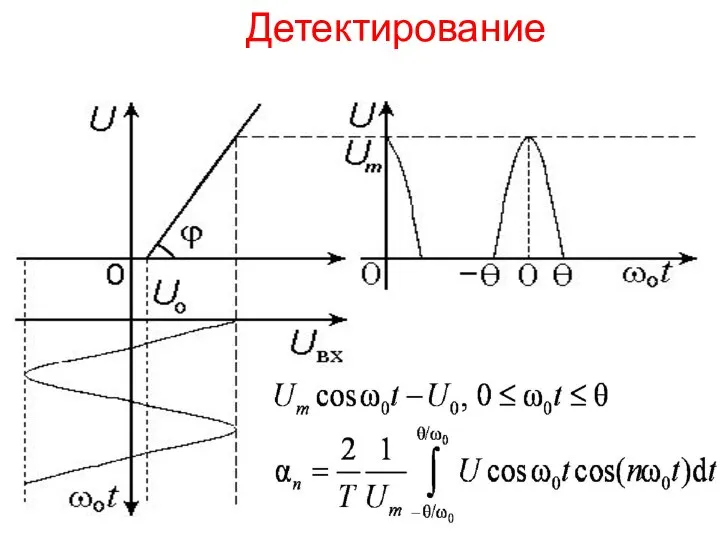 Детектирование. Функции и коэффициенты Берга
Детектирование. Функции и коэффициенты Берга Математическая игра-раскраска Обезьянка
Математическая игра-раскраска Обезьянка Структура арифметической задачи
Структура арифметической задачи Графический диктант Раскрытие скобок
Графический диктант Раскрытие скобок Эконометрика. Оценка влияния количественных показателей друг на друга
Эконометрика. Оценка влияния количественных показателей друг на друга Презентация на тему Формулы суммы и разности синуса и косинуса
Презентация на тему Формулы суммы и разности синуса и косинуса  Перпендикулярность прямых, прямой и плоскости
Перпендикулярность прямых, прямой и плоскости Корреляционный анализ. Тема 9
Корреляционный анализ. Тема 9 Упражнения по планиметрии на готовых чертежах. VII класс
Упражнения по планиметрии на готовых чертежах. VII класс Определение длины остряков и тяговых усилий для их перевода
Определение длины остряков и тяговых усилий для их перевода