Содержание
- 2. Гамма-функция Интегральное представление:
- 3. Основное свойство : Γ(x+1) = x Γ(x) где х – любое действительное число. Частные свойства. Γ(n+1)
- 4. Асимптотика
- 5. График функции Γ(x). Интервал: [ - 1; 1].
- 6. График функции Γ(x). Интервал: [ - 5; 5].
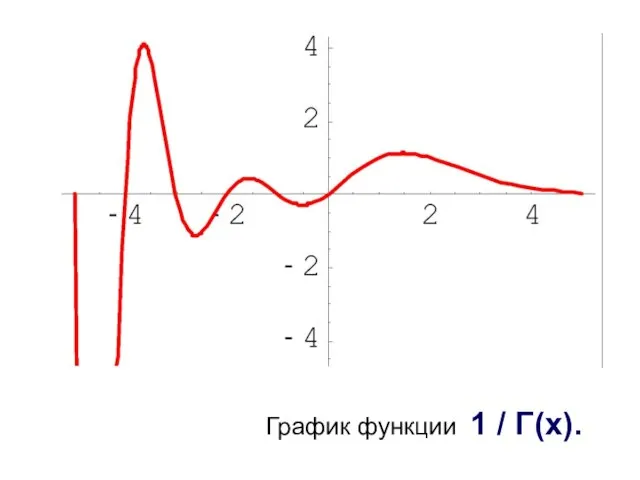
- 7. График функции 1 / Γ(x).
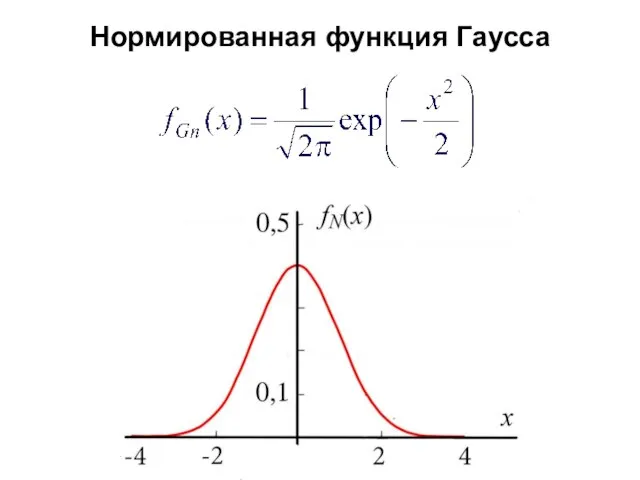
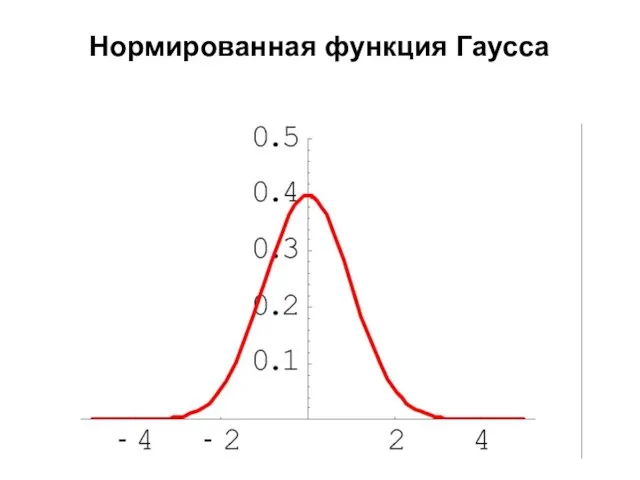
- 8. Нормированная функция Гаусса
- 9. Случайная величина «хи-квадрат» где ξi – независимые случайные величины, каждая из которых имеет нормальное нормированное распределение
- 10. Вид распределения зависит от целочисленного параметра ν, который называется число степеней свободы и принимает значения натурального
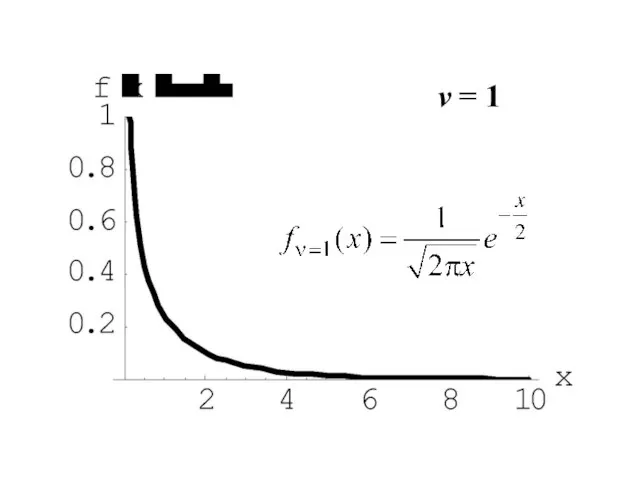
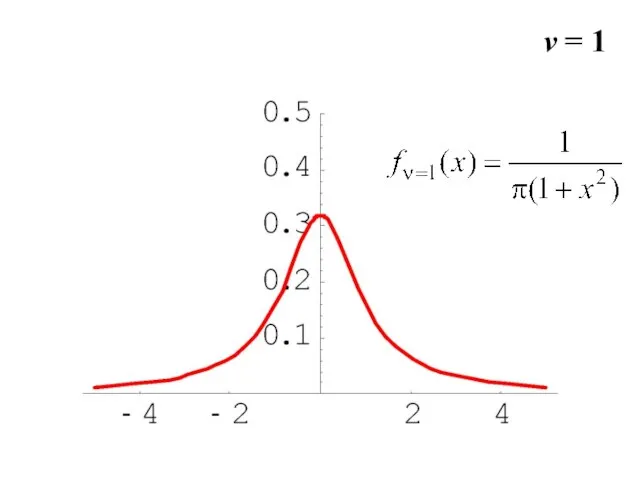
- 11. v = 1
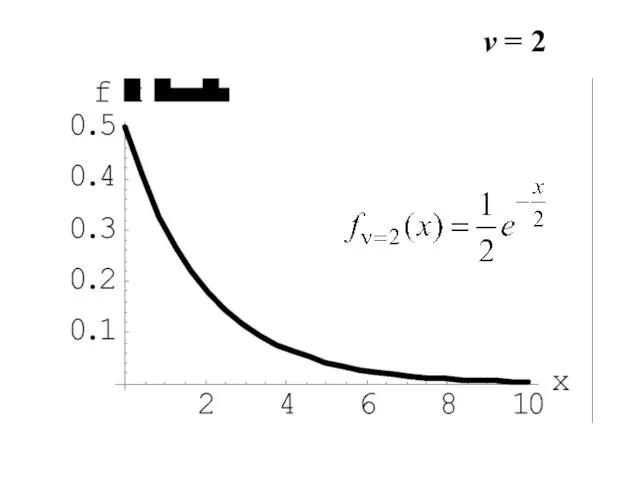
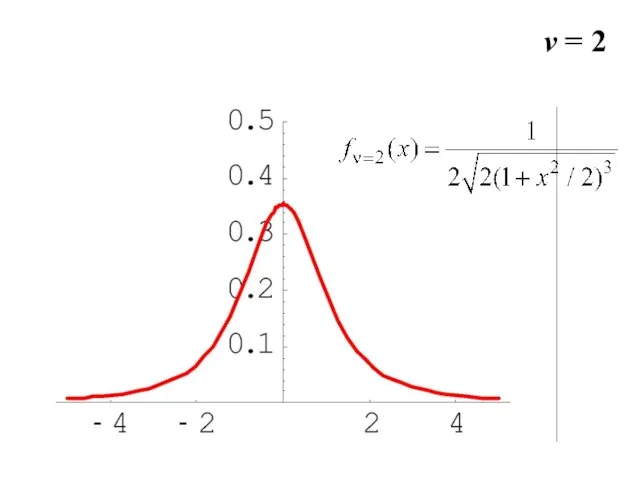
- 12. v = 2
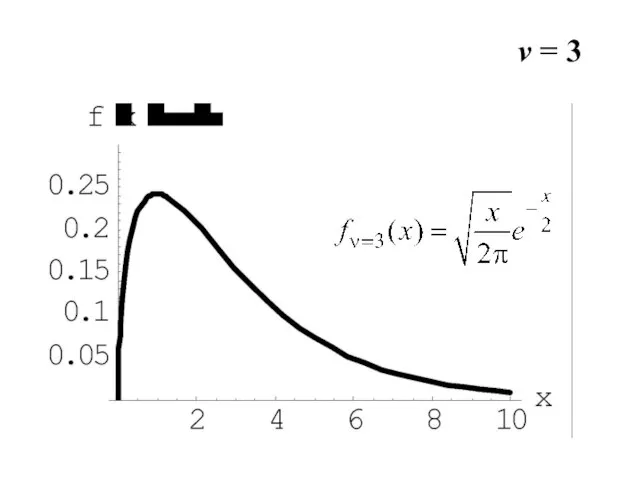
- 13. v = 3
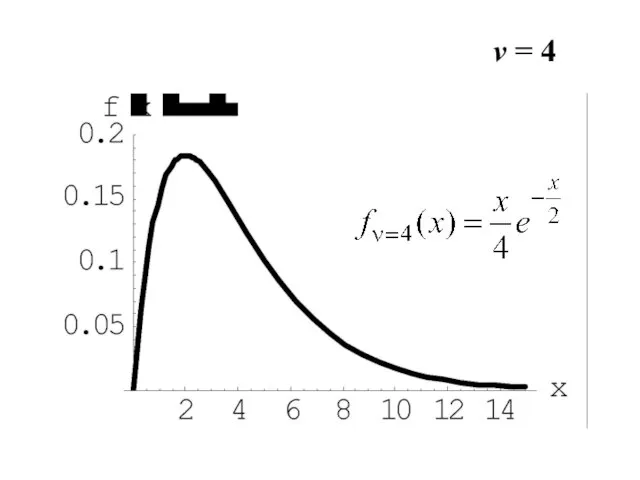
- 14. v = 4
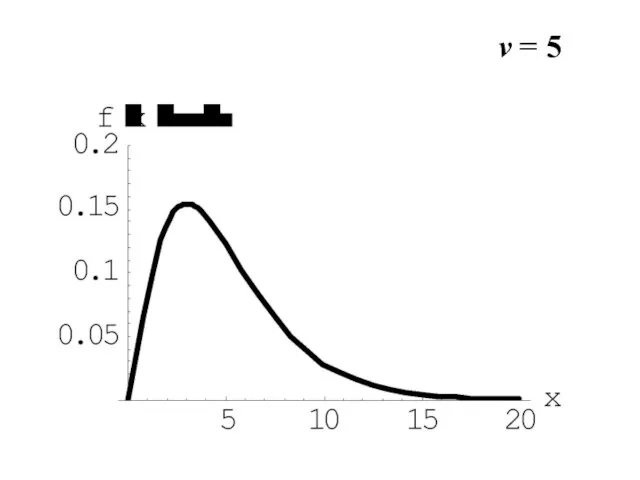
- 15. v = 5
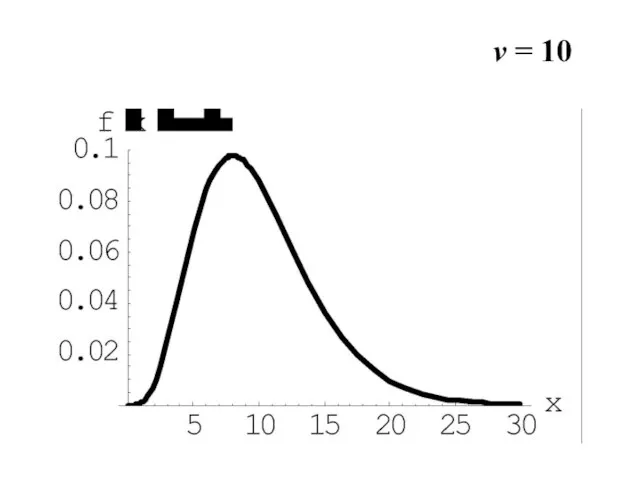
- 16. v = 10
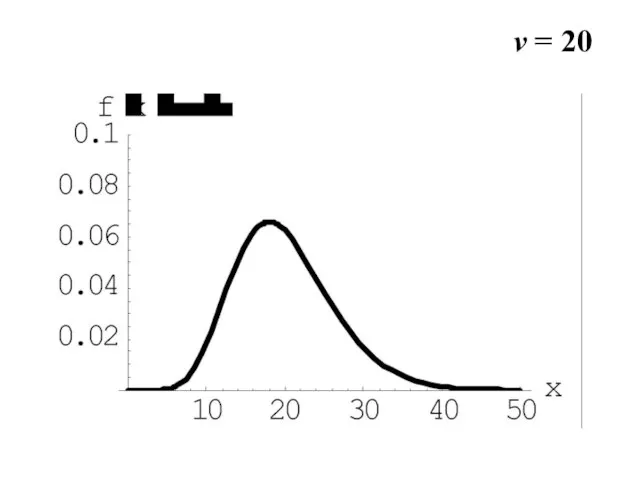
- 17. v = 20
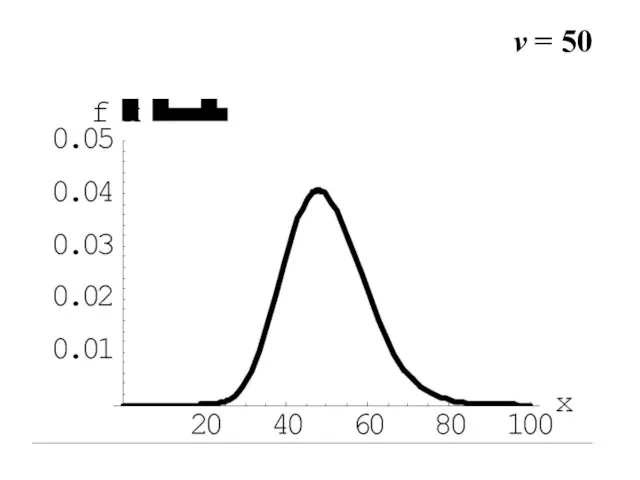
- 18. v = 50
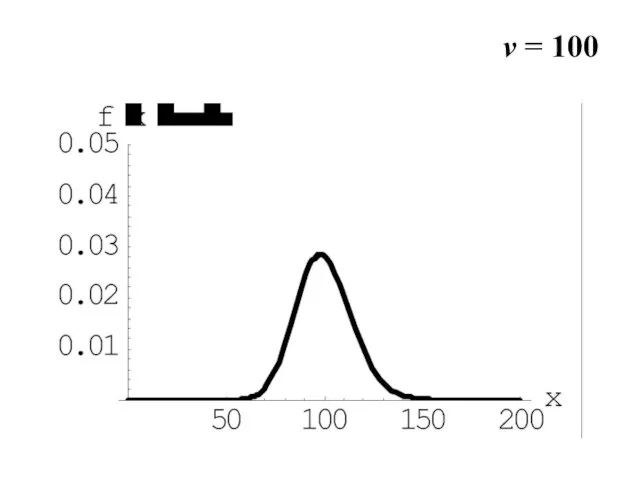
- 19. v = 100
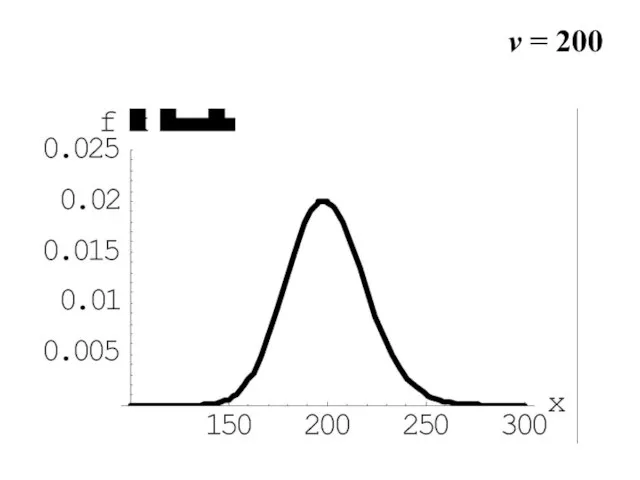
- 20. v = 200
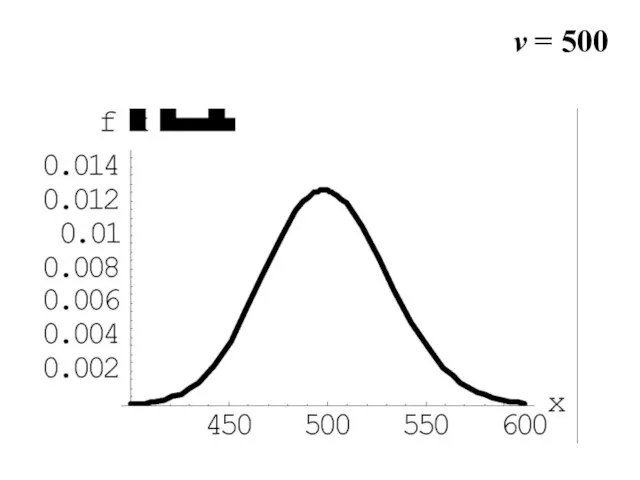
- 21. v = 500
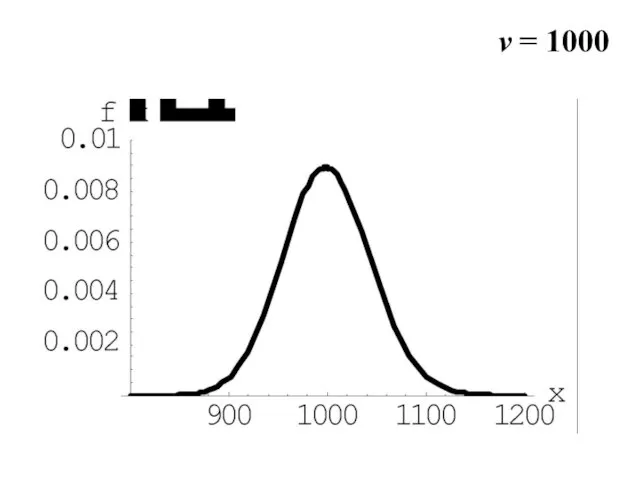
- 22. v = 1000
- 23. при v → ∞ превращается в гауссову нормированную случайную величину.
- 24. Случайная величина Стьюдента где все (ν + 1) случайные величины ξi независимы и имеют нормальное нормированное
- 25. Плотность случайной величины Стьюдента Вид распределения зависит от числа степеней свободы M(Tv) = 0 Математическое ожидание
- 26. v = 1
- 27. v = 2
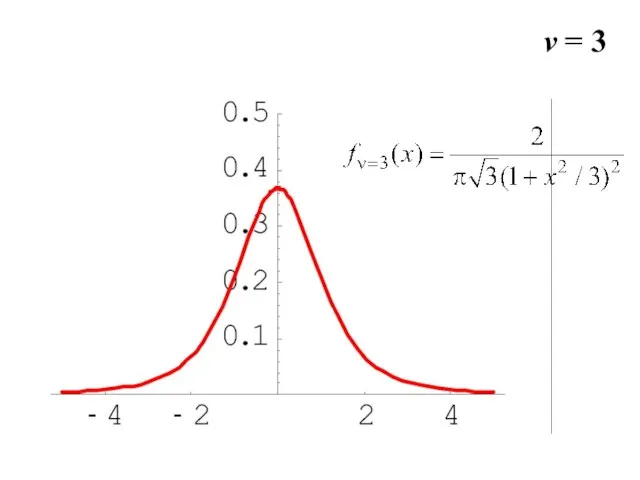
- 28. v = 3
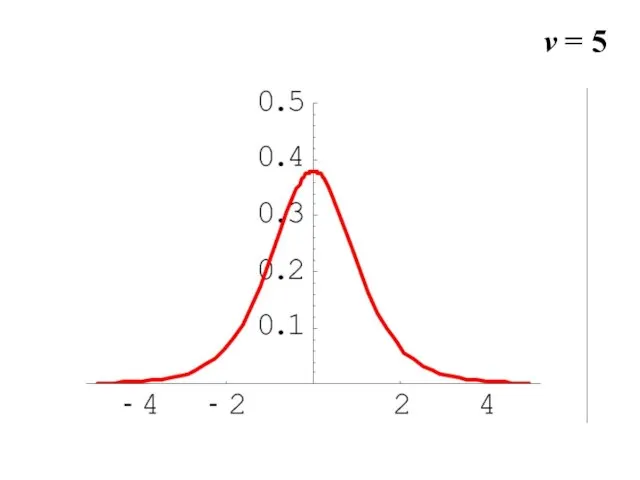
- 29. v = 5
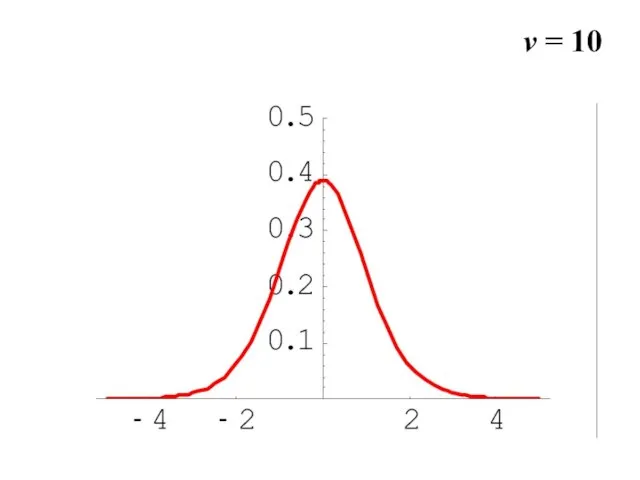
- 30. v = 10
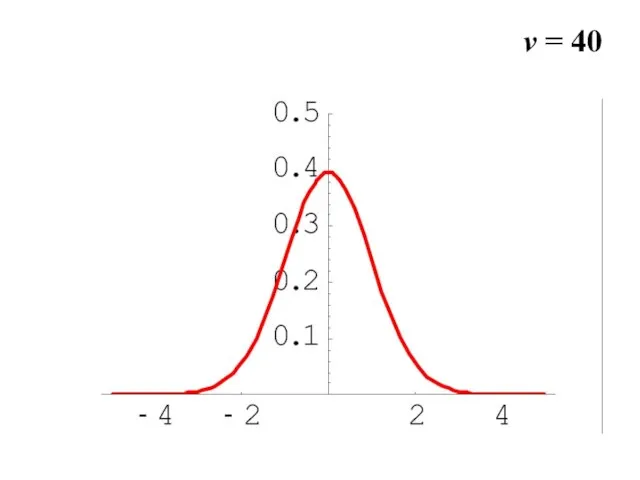
- 31. v = 40
- 32. Нормированная функция Гаусса
- 34. Скачать презентацию



![График функции Γ(x). Интервал: [ - 1; 1].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/914352/slide-4.jpg)
![График функции Γ(x). Интервал: [ - 5; 5].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/914352/slide-5.jpg)





 Функции многих переменных. Лекция 16
Функции многих переменных. Лекция 16 Выдающиеся российские математики. Урок-лекция, 5- 11 кл
Выдающиеся российские математики. Урок-лекция, 5- 11 кл Тригонометрия. Математика с Д.А. Власовым
Тригонометрия. Математика с Д.А. Власовым Центральная и осевая симметрия
Центральная и осевая симметрия Единицы стоимости. Рубль, копейка
Единицы стоимости. Рубль, копейка Умножение десятичной дроби на натуральное число. Графический диктант
Умножение десятичной дроби на натуральное число. Графический диктант Тригонометрические функции
Тригонометрические функции Презентация по математике. Исторические сведения
Презентация по математике. Исторические сведения Линейная регрессия
Линейная регрессия Презентация на тему Прямоугольный параллелепипед. Куб
Презентация на тему Прямоугольный параллелепипед. Куб  Отбор корней в тригонометрическом уравнении
Отбор корней в тригонометрическом уравнении Предел функции в точке и на бесконечности
Предел функции в точке и на бесконечности Элементы линейной алгебры. Матрицы. Определители
Элементы линейной алгебры. Матрицы. Определители Предел функции (часть 2)
Предел функции (часть 2) Пирамида. Определение пирамиды. Виды пирамид
Пирамида. Определение пирамиды. Виды пирамид Теорема Пифагора
Теорема Пифагора Старинные задачки по математике
Старинные задачки по математике Простейшие преобразования графиков
Простейшие преобразования графиков Инструкция по изготовлению трубогранника. Тетраэдр
Инструкция по изготовлению трубогранника. Тетраэдр Теорема косинусов
Теорема косинусов Страна Математика
Страна Математика Интервальное оценивание параметров распределения случайных величин. Доверительный интервал
Интервальное оценивание параметров распределения случайных величин. Доверительный интервал Части задачи
Части задачи Числовые выражения
Числовые выражения Логарифмы и их свойства
Логарифмы и их свойства Презентация по математике "Пропорциональные величины" -
Презентация по математике "Пропорциональные величины" -  Всегда ли симметрично - это хорошо?
Всегда ли симметрично - это хорошо? График кусочно гладкой функции
График кусочно гладкой функции