Содержание
- 2. Скалярное произведение векторов – число (скаляр). Скалярным произведением двух векторов называется произведение их длин на косинус
- 3. Формула для нахождения скалярного произведения через координаты векторов = x1x2 + y1y2 + z1z2
- 4. Пример №1 Найти скалярное произведение векторов: a {-6; 9; 5} b {-1; 0; 7}
- 5. Пример №2 Найти скалярное произведение векторов: a {0; 0; 4} b {22; 1; 8}
- 6. Пример №3 Найти скалярное произведение векторов: a {1; 7; 9} b {-2; 4; 0}
- 7. Косинус угла между векторами № 4
- 8. № 5
- 9. Дано: Найти: угол между прямыми АВ и CD. Ваши предложения… Найдем координаты векторов и 2. Воспользуемся
- 11. Скачать презентацию






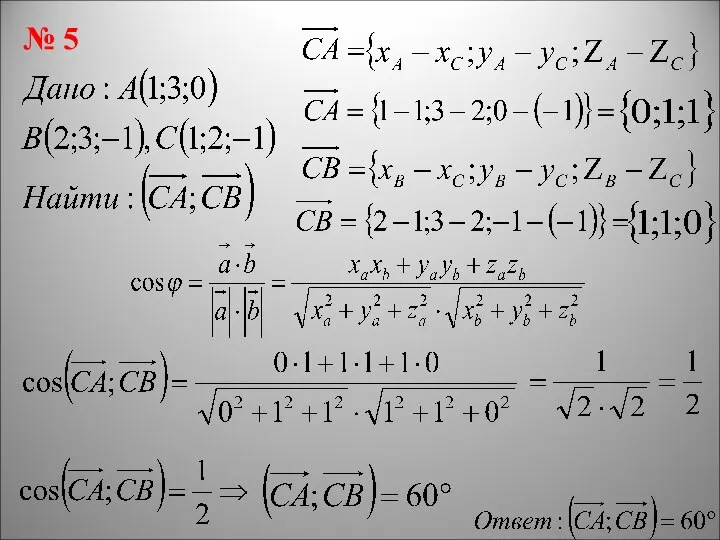

 Решение задач геометрия
Решение задач геометрия Элементы математической статистики. Лекция 1
Элементы математической статистики. Лекция 1 ЕГЭ Профиль. Решение задания №12
ЕГЭ Профиль. Решение задания №12 Истинностные задачи
Истинностные задачи задача про арбузы2
задача про арбузы2 Предел функции. Раскрытие неопределенности
Предел функции. Раскрытие неопределенности Применение теории вероятностей в анализе спортивных событий
Применение теории вероятностей в анализе спортивных событий Пирамида. Правильная пирамида
Пирамида. Правильная пирамида Профессия математик - инновационные сферы применения знаний Исследователь: ученик 10 класса Романенко Николай Руководитель: уч
Профессия математик - инновационные сферы применения знаний Исследователь: ученик 10 класса Романенко Николай Руководитель: уч Действия над комплексными числами
Действия над комплексными числами Разделительное свойство умножения
Разделительное свойство умножения Урок 9-10 Відстань між двома точками на площині
Урок 9-10 Відстань між двома точками на площині Построение таблиц истинности
Построение таблиц истинности Математична гра Я – підприємець
Математична гра Я – підприємець Решение задач
Решение задач Бинарные отношения
Бинарные отношения Квадратичная функция и ее свойства
Квадратичная функция и ее свойства Треугольники (элементы, площади)
Треугольники (элементы, площади) Построение сечений
Построение сечений Путешествие по морям
Путешествие по морям Презентация на тему Решето Эратосфена
Презентация на тему Решето Эратосфена  Презентация на тему Комбинации шара с многогранниками и фигурами вращения
Презентация на тему Комбинации шара с многогранниками и фигурами вращения  Планиметрия. Решение прямоугольного треугольника
Планиметрия. Решение прямоугольного треугольника Функциональная грамотность на уроках математики начальных классов
Функциональная грамотность на уроках математики начальных классов Свойство биссектрисы угла
Свойство биссектрисы угла Статистическая сводка и группировка
Статистическая сводка и группировка Теорема Пифагора
Теорема Пифагора Теория расписаний. Минимизация приоритето-порождающих функций
Теория расписаний. Минимизация приоритето-порождающих функций