Содержание
- 2. Иррациональным уравнением называется уравнение, в которых переменная «x»содержится под знаком корня. Например,
- 3. Какие из уравнений не являются иррациональными?
- 4. Идея решения Главный способ избавиться от корня и получить рациональное уравнение – возведение обеих частей уравнения
- 5. Основные методы решения иррациональных уравнений: возведение в степень обеих частей уравнения; введение новой переменной; разложение на
- 6. Метод возведения в степень обеих частей уравнения: 1) Если иррациональное уравнение содержит только один радикал, то
- 7. Метод возведения в степень обеих частей уравнения: 2) Если в иррациональном уравнении содержится два или более
- 9. Запомни! При возведении обеих частей уравнения • в четную степень (показатель корня – четное число) –
- 13. 1 способ 2 способ Пример №4
- 15. Пример №5
- 16. Пример №6
- 20. Метод введения новой переменной Данный метод применяется в том случае, когда в уравнении неоднократно встречается некоторое
- 25. Метод разложения на множители Для решения иррациональных уравнений данным методом следует пользоваться правилом: Произведение равно нулю
- 29. Дополнительные методы решения иррациональных уравнений: метод «пристального взгляда» (метод анализа уравнения); использование монотонности функции; переход к
- 30. Метод анализа уравнения Свойства корней, которые используют при решении уравнений данным способом: 1. Все корни четной
- 33. Метод использования монотонности функции Сформулируем два свойства монотонных функций: 1. Сумма возрастающих (убывающих) функций – функция
- 34. Метод использования монотонности функций Теорема о корне Пусть y=f(x) – монотонная на некотором промежутке функция. Тогда
- 36. Метод перехода к уравнению с модулем
- 39. Скачать презентацию









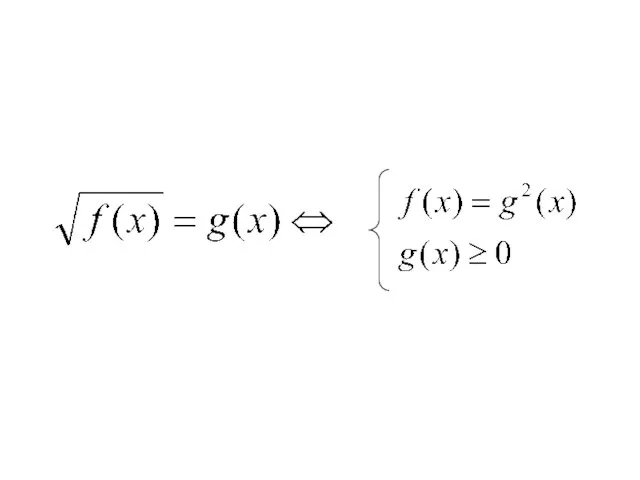


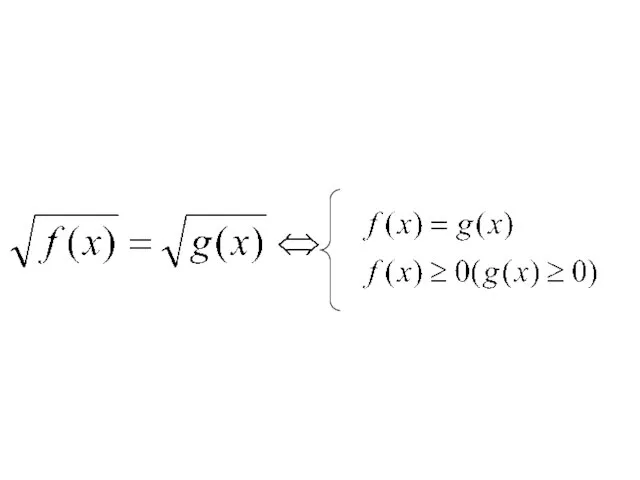























 Решение заданий ЕГЭ уровня С2 (1 часть)
Решение заданий ЕГЭ уровня С2 (1 часть) Сочетательное и распределительное свойство умножения. Урок 1
Сочетательное и распределительное свойство умножения. Урок 1 Признаки делимости на 2, 5,10, 3, 6 и 9
Признаки делимости на 2, 5,10, 3, 6 и 9 Параллельные прямые в пространстве
Параллельные прямые в пространстве Неопределенный интеграл
Неопределенный интеграл Урок 53. Расстояние от точки до прямой
Урок 53. Расстояние от точки до прямой Степень с рациональным показателем
Степень с рациональным показателем Косинус угла
Косинус угла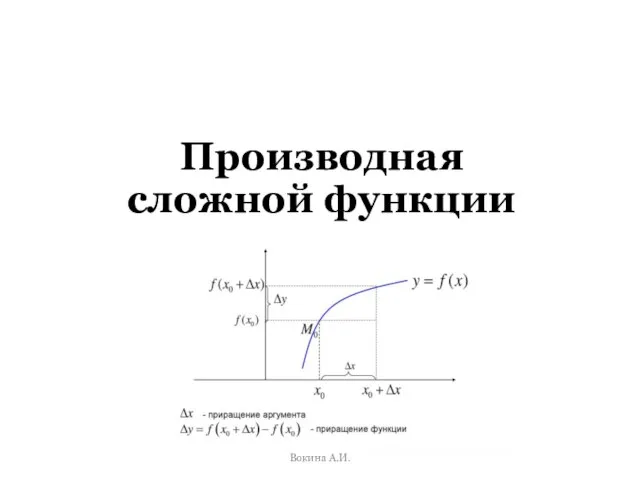 Производная сложной функции
Производная сложной функции Понятие вектора
Понятие вектора Определители. Матрица и ее определитель
Определители. Матрица и ее определитель Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейших тригонометрических уравнений с помощью единичной окружности Задания на развитие логики
Задания на развитие логики 20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами
20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами Деловая игра Маркетинг инноваций
Деловая игра Маркетинг инноваций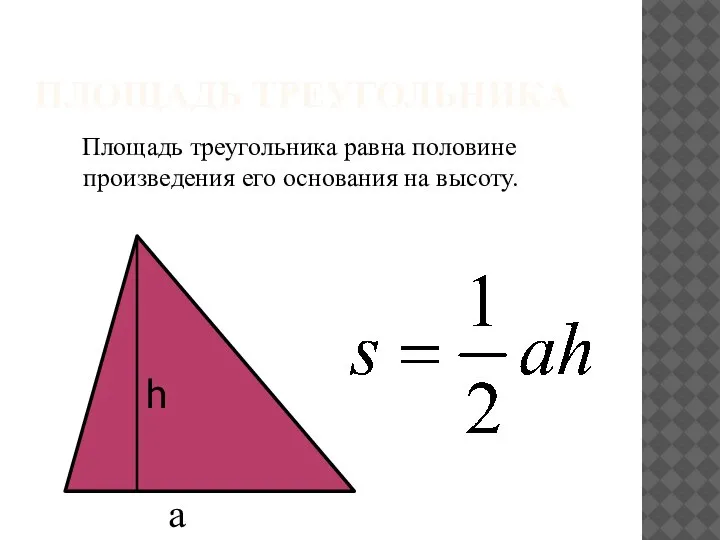 Площадь треугольника
Площадь треугольника Математика без границ. Конкурс
Математика без границ. Конкурс Сантиметр. Линейка
Сантиметр. Линейка Золотое сечение
Золотое сечение Информатика. Вероятность
Информатика. Вероятность Загадки и тайны треугольника
Загадки и тайны треугольника Сложение вида + 2, + 3
Сложение вида + 2, + 3 Презентация на тему Признаки равенства треугольников
Презентация на тему Признаки равенства треугольников  Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике)
Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике) Умножение одночлена на многочлен
Умножение одночлена на многочлен Современная финансовая математика
Современная финансовая математика Элементы круга и окружности в задачах ОГЭ
Элементы круга и окружности в задачах ОГЭ Плоскость и прямая в пространстве
Плоскость и прямая в пространстве