Статистические гипотезы

Проверка статистической гипотезы состоит в выяснении совместимости выдвинутого предположения с результатами наблюдений.
Проверка гипотезы базируется на полученной выборке.
Всегда возможно расхождение между теоретическим предположением и результатами измерений из-за того, что элементы выборки – случайные величины.
Поэтому, при малых расхождениях теоретических и экспериментальных величин отвергать гипотезу не следует.

Необходимо определить, какие расхождения можно полагать пренебрежимо малыми, а какие – существенными для отбрасывания выдвинутой гипотезы.
Так как элементы выборки (результаты экспериментов) являются случайными величинами, то определенной величине расхождения соответствует некоторая вероятность.
Следовательно, выводы о принятии и отвержении гипотезы утверждаются с некоторой вероятностью.

Выводы о результате проверки статистической гипотезы основаны на принципе практической невозможности.
«Случайное событие с малой вероятностью в однократном испытании произойти не может» (Чебышев, 1845г.).

Уровень значимости α.
Величина α – вероятность практически невозможного события в однократном испытании.
Если вероятность различия теоретических и экспериментальных результатов окажется меньше величины α, то это различие объясняется флуктуациями элементов выборки и объявляется «незначимым».
Статистическая гипотеза принимается с вероятностью
η = 1 – α.

В противоположном случае, когда вероятность различия теоретических и экспериментальных результатов больше величины α, то различие эмпирического и теоретического распределений объявляется «значимым», т.е. необъяснимым флуктуациями элементов выборки.
Тогда выдвинутая гипотеза отвергается на принятом уровне значимости α.

Начальная гипотеза, которая проверяется называется нулевой H0
Принятие или отбрасывание нулевой гипотезы осуществляется с помощью некоторого критерия.
Критерием K называется некоторая статистика (т.е. случайная величина, построенная из элементов выборки), чей закон распределения вероятности известен из теории вероятностей.
На множестве всевозможных значений критерия {K} выделяется подмножество {K0} , называемое критической областью.

Критическая область строится так, чтобы вероятность попадания случайного значения критерия K в область {K0} (при условии справедливости нулевой гипотезы) равнялась выбранному уровню значимости α.
P[ K∈{K0}: H0 ] = α (1)

Алгоритм проверки статистической гипотезы
Формулируется нулевая гипотеза H0.
Выбирается уровень значимости α.
Определяется критическая область {K0} ,
Вычисляется значение критерия K* на базе полученной выборки.
Проверяется попадание вычисленного значения K* в критическую область {K0}.
При попадании (K*∈{K0}) нулевая гипотеза H0 отвергается.
В противоположном случае – нулевая гипотеза H0 не отвергается (т.е. принимается).

Статистические ошибки 1-го рода и 2-го рода
Выдвинутая статистическая гипотеза называется нулевой.
Ошибка 1-го рода: отбрасывание истинной гипотезы. Равна выбранному уровню значимости α.
Кроме нулевой гипотезы всегда существует альтернативная гипотеза.
Ошибка 2-го рода: принятие нулевой гипотезы, когда она ложна (т.е. когда верна альтернативная гипотеза).

При выборе критической области (при фиксированном уровне значимости α) необходимо максимально уменьшать ошибку 2-го рода:
P[ K∉{K0}: H1 ] = β (2)
Вероятность P[ K∈{K0}: H1 ] = 1 − β (3)
называется мощностью критерия.

Практически всегда при уменьшении ошибки 1-го рода α начинает возрастать ошибка 2-го рода. Поэтому требуется искать компромисс между величинами ошибок 1-го рода и 2-го рода.
В частности, если P[ K∈{K0}: H1 ] ≤ α , то отвергать нулевую гипотезу H0 в пользу альтернативной H1 было бы принципиально неверно, так как вероятность события K∈{K0} при альтернативной гипотезе H1 еще меньше, чем при нулевой гипотезе H0 .

Наилучшим для проверки статистической гипотезы было бы такое критическое событие, которое имело бы малую вероятность при нулевой гипотезе H0 и большую вероятность при альтернативной гипотезе H1 .
P[ K∈ {K0}: H0 ] = α (1)
P[ K∈ {K0}: H1 ] = 1 - β (3)

Критерий согласия
Пирсона
Критерий «хи-квадрат»

Область изменения значений генеральной совокупности разбивается на R конечных интервалов sk (k = 1, 2, …, R).
Для каждого интервала подсчитываются:
во-первых, вероятность попадания значения случайной величины в данный интервал :
pk = P[x ∈ sk] k = 1, 2, …, R (4)
во-вторых, частота попадания в данный интервал элементов полученной выборки:
νk = nk / n k = 1, 2, …, R (5)

Критерий Пирсона задается формулой
Частоты (5) – случайные величины. Следовательно, величина (6) – случайная.
(6)

Теорема Пирсона.
Случайная величина (6) при n → ∞ , имеет распределение «хи-квадрат» c числом степеней свободы: R – 1

Гипотетические распределения в практических задачах часто содержат параметры.
Неизвестные генеральные значения параметров приходится заменять их оценками, полученными из выборки.
Тогда вероятности, вычисленные по формулам (4) получат случайный разброс.
Каков тогда закон распределения критерия (6) ?

Теорема Фишера.
Случайная величина (5) при n → ∞ имеет распределение «хи-квадрат» с числом степеней свободы
R – 1 – q , (7)
где q – количество параметров генерального распределения, которые заменены выборочными точечными оценками.

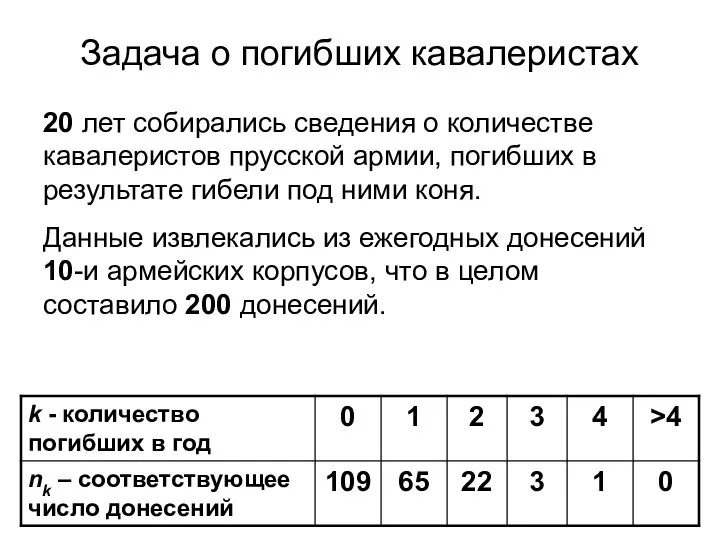
Задача о погибших кавалеристах
20 лет собирались сведения о количестве кавалеристов прусской армии, погибших в результате гибели под ними коня.
Данные извлекались из ежегодных донесений 10-и армейских корпусов, что в целом составило 200 донесений.

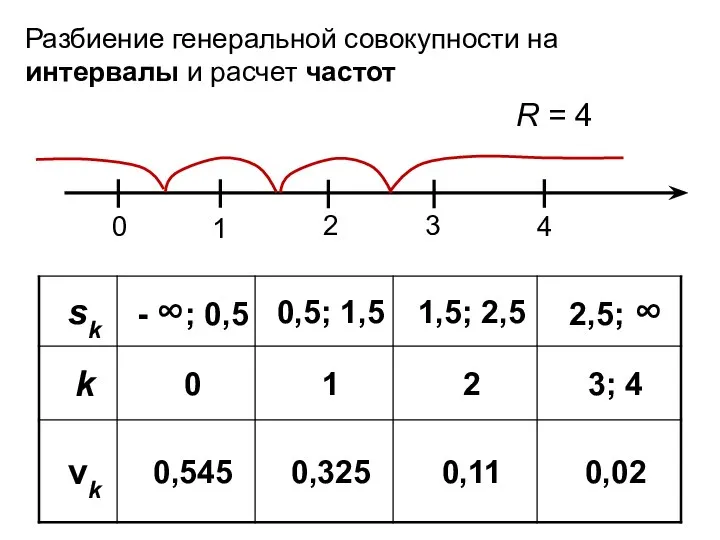
Разбиение генеральной совокупности на интервалы и расчет частот
R = 4

Нулевая гипотеза H0:
Распределение погибших подчиняется закону Пуассона
Параметр a по смыслу является математическим ожиданием пуассоновской случайной величины и его значение неизвестно.
(8)

Заменим неизвестный параметр a его приближенным значением – средним статистическим
(9)
(10)

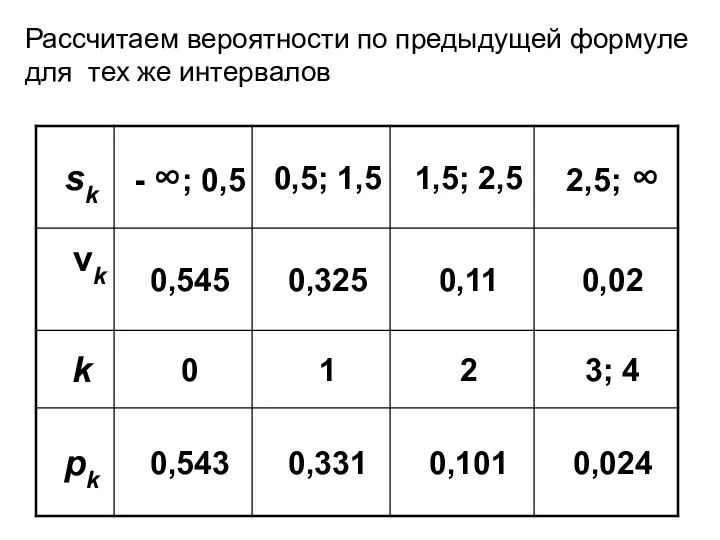
Рассчитаем вероятности по предыдущей формуле для тех же интервалов

Вычислим значение критерия Пирсона по данным таблицы
(11)

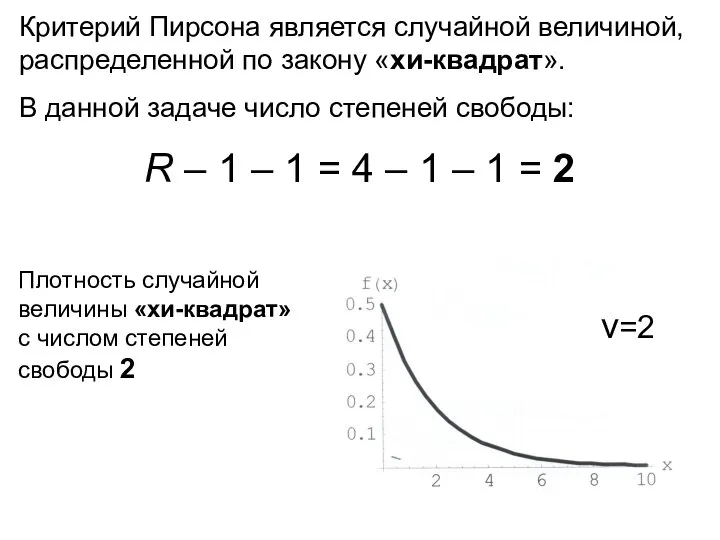
Критерий Пирсона является случайной величиной, распределенной по закону «хи-квадрат».
В данной задаче число степеней свободы:
R – 1 – 1 = 4 – 1 – 1 = 2
Плотность случайной величины «хи-квадрат»
с числом степеней свободы 2
ν=2

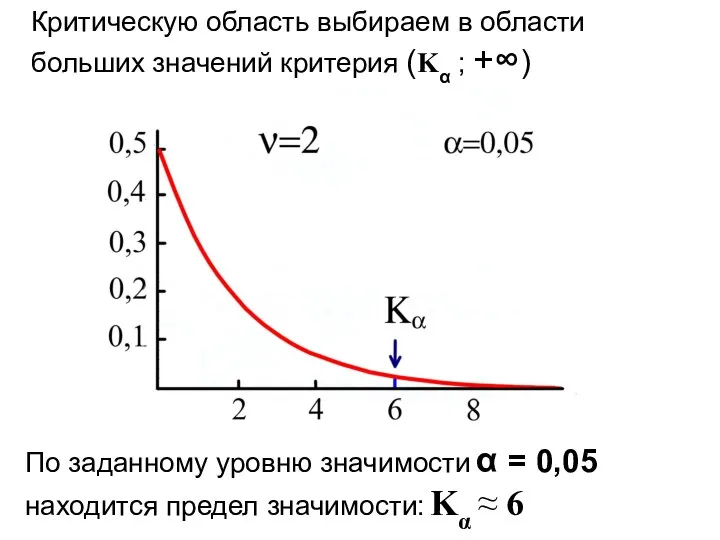
Критическую область выбираем в области больших значений критерия (Kα ; +∞)
По заданному уровню значимости α = 0,05 находится предел значимости: Kα ≈ 6

Сравнение значения критерия K* = 0,32
с пределом значимости Kα = 6
позволяет принять нулевую гипотезу H0.

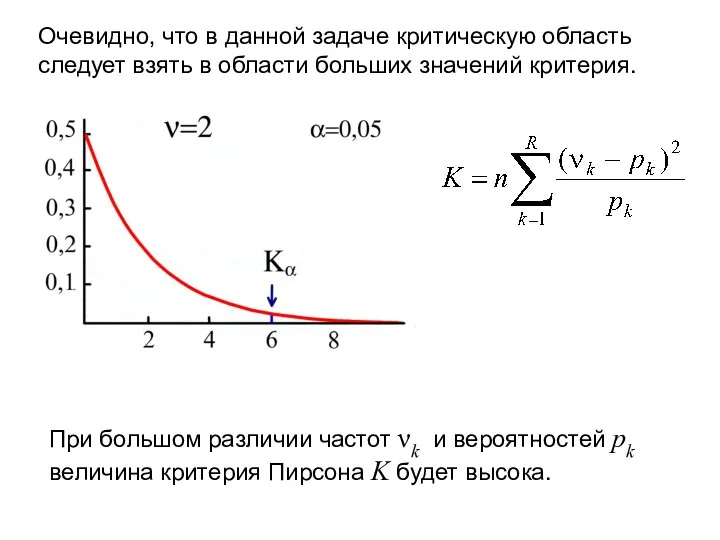
Очевидно, что в данной задаче критическую область следует взять в области больших значений критерия.
При большом различии частот νk и вероятностей pk величина критерия Пирсона K будет высока.