Комбинаторные задачи

Повторение
1. Чему равен периметр восьмиугольника, каждая сторона которого равна 4 см?
2. Вычислите сумму
27 + 16 + 33 + 24.
3. Из цифр 8, 9, 4 составили трёхзначные числа. Сколько чисел получится и какие это числа, если цифры не повторяются?

Ответы
32 см.
100.
6 чисел: 894, 849, 984, 948, 489, 498.

Предположим, вам нужно позвонить другу, но вы не можете вспомнить последнюю цифру номера телефона. Какое наибольшее количество номеров придётся набрать, чтобы дозвониться до друга?

Поскольку в конце номера может стоять любая из 10 цифр, то вам в худшем случае придётся сделать 10 попыток, тем самым перебрав все возможные варианты.

Нередко в повседневной жизни мы встречаемся с задачами, решение которых требует рассмотрения всех возможных случаев, или, как ещё принято говорить, всех возможных комбинаций. Поэтому такие задачи называют комбинаторными.

Комбинаторные
задачи

Раздел математики,
в котором изучают
комбинаторные задачи,
называется
комбинаторикой

Познакомимся с некоторыми
приемами решения комбинаторных задач
решение методом перебора;
решение с помощью дерева возможных вариантов;
решение с помощью комбинаторного правила умножения;
решение с помощью таблиц;
решение с помощью графов.

1. Метод перебора

1. У Ирины 5 подруг: Вера, Зоя, Марина, Полина и Светлана. Она решила двух из них пригласить в кино. Укажите все возможные варианты выбора подруг. Сколько таких вариантов?
Замечание. При решении для краткости будем писать первые буквы имен.

Составим сначала все пары, в которые входит Вера.
ВЗ, ВМ, ВП, ВС
Выпишем теперь пары, в которые входит Зоя, но не входит Вера.
Далее составим пары, в которые входит Марина, но не входят Вера и Зоя.
Еще одна пара
ЗМ, ЗП, ЗС
МП, МС
ПС
Всего существует 4+3+2+1=10
Решение
Ответ:10 вариантов
Вера
Зоя
Марина
Полина
Света
Получим 4 пары.
Таких пар три.
Их две.
Далее составим пары, в которые входит Полина.

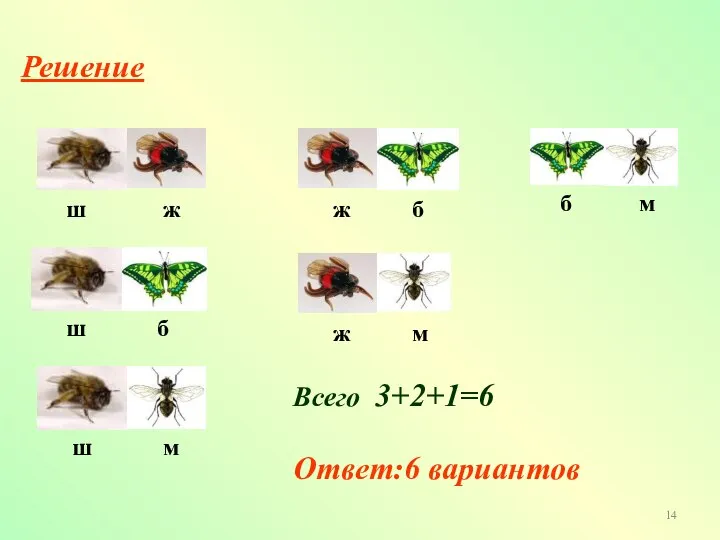
Рассмотрим еще одну задачу. 2. На цветочной клумбе сидели шмель, жук, бабочка и муха. Два насекомых улетели. Какие пары насекомых могли улететь? Укажите все возможные варианты. Сколько таких вариантов?
Способ рассуждений, которым мы воспользовались при решении задачи, называют перебором возможных вариантов.
ш
ж
б
м

Решение
Всего 3+2+1=6
Ответ:6 вариантов
ш
ш
ш
ж
ж
б
б
б
ж
м
м
м

Таким образом, из трёх данных цифр можно составить всего 9 различных двузначных чисел.
Ответ: 9 чисел.
Приемы решения комбинаторных задач
метод перебора
11;14;17; (начали с 1)
Решение: Для того, чтобы не пропустить и не повторить ни одного из чисел, будем выписывать их в порядке возрастания:
3. Сколько двузначных чисел можно составить, используя цифры 1; 4; 7?
41;44;47; (начали с 4)
71;74;77; (начали с 7)

2. Метод «Дерево возможных вариантов.»

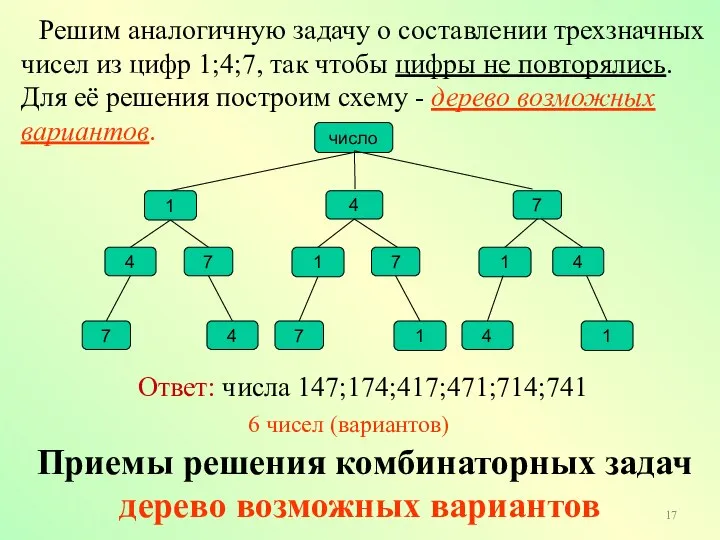
Приемы решения комбинаторных задач дерево возможных вариантов
Решим аналогичную задачу о составлении трехзначных чисел из цифр 1;4;7, так чтобы цифры не повторялись. Для её решения построим схему - дерево возможных вариантов.
число
1
4
7
4
4
7
7
1
1
7
7
1
1
4
4
Ответ: числа 147;174;417;471;714;741
6 чисел (вариантов)

Заметим, что ответ на вопрос, можно получить, не выписывая сами числа. Будем рассуждать так.
Первую цифру можно выбрать тремя способами. Так как после выбора первой цифры останутся две, то вторую цифру можно выбрать двумя способами. Остается приписать одну цифру. Следовательно, общее число искомых трехзначных чисел равно произведению

3. Мы получили правило комбинаторного умножения

У Куклы Светы 3 юбки и 5 кофт, удачно сочетающихся по цвету. Сколько различных комбинаций одежды имеется у Светы?
Решение. 3·5 = 15
комбинаторное правило умножения

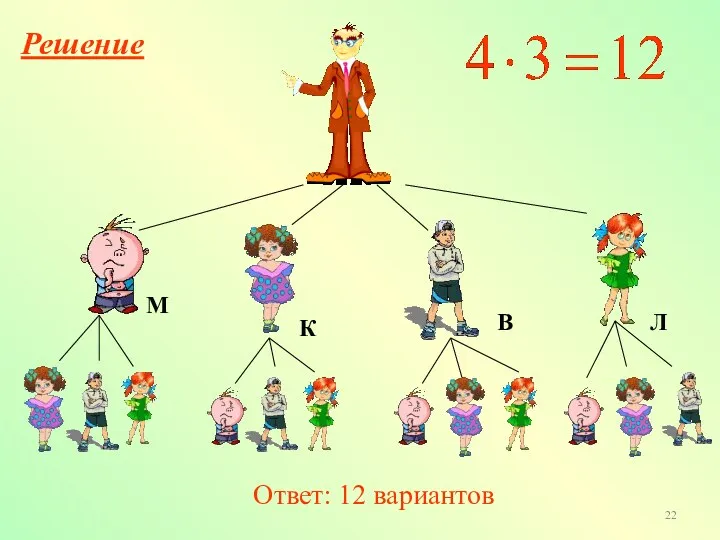
Решите задачу, используя
дерево возможных вариантов
В класс пришли четыре новых ученика Миша, Катя, Вася, Лиза. С помощью дерева возможных вариантов покажи, все возможные варианты расположения четырех учеников за одной партой. Сколько вариантов выбора будет?
Л
В
К
М

Ответ: 12 вариантов
Решение
М
В
К
Л

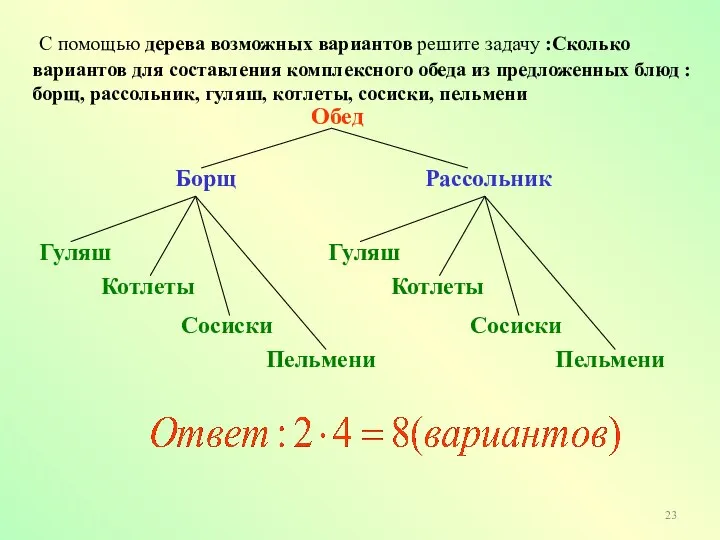
С помощью дерева возможных вариантов решите задачу :Сколько вариантов для составления комплексного обеда из предложенных блюд : борщ, рассольник, гуляш, котлеты, сосиски, пельмени
Котлеты
Гуляш
Рассольник
Борщ
Обед
Пельмени
Сосиски
Котлеты
Гуляш
Пельмени
Сосиски

4. Метод «Составление таблицы»

У Миши 4 ручки разного цвета и 3 блокнота разного размера. Сколько различных наборов из ручки и блокнота сможет составить Миша? Реши задачу, составив таблицу.
Приемы решения комбинаторных задач
задачи, решаемые с помощью таблиц
м
с
б
с
з
ч
к

12 различных наборов
м
с
б
з
ч
к
с