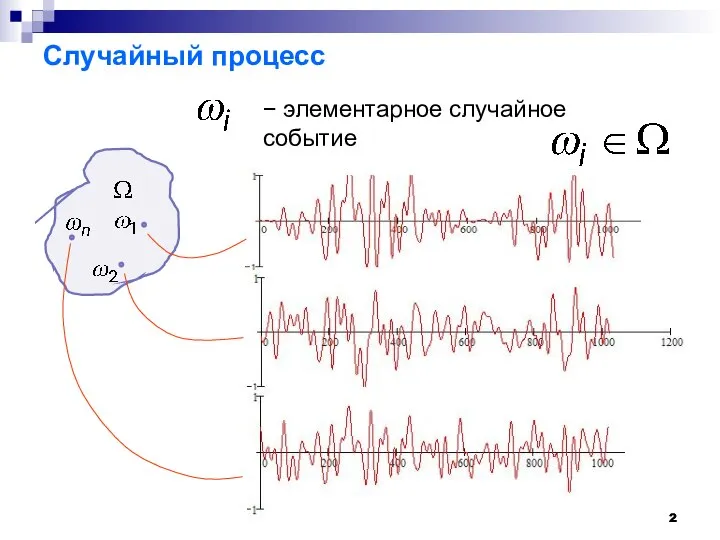
08_ ОТС_ Основы теории СП-2

Случайный процесс
− элементарное случайное событие

Случайный процесс считается полностью определенным, если для любого
Случайные процессы
Перейти от описания с.в. к описанию с.п. можно, рассматривая совместные распределения двух, трех и т.д. значений
процесса в некоторые различные моменты времени
Зависимость от времени явно не указана для упрощения записи
условие нормировки
можно записать его совместную ПРВ при любом выборе моментов времени

Числовые характеристики СП
смешанные начальные моменты
В частности, при ,
получается математическое ожидание в сечении
При
,
дисперсия в сечении
и т.д.
смешанные центральные моменты

Моментные функции
В общем случае моменты совместной ПРВ зависят от расположения сечений на оси времени и называются моментными функциями.
− функция автокорреляции, или автокорреляционная функция (АКФ)
здесь и далее явно не указана зависимость от времени, в частности, функциями времени являются
и
Чаще всего используют второй смешанный центральный момент

Полное описание такой пары − совместная ПРВ отсчетов первого СП и отсчетов второго процесса при любых и
Совместное описание двух СП
− взаимно корреляционная функция
Числовые характеристики − всевозможные смешанные моменты, наиболее широко используется

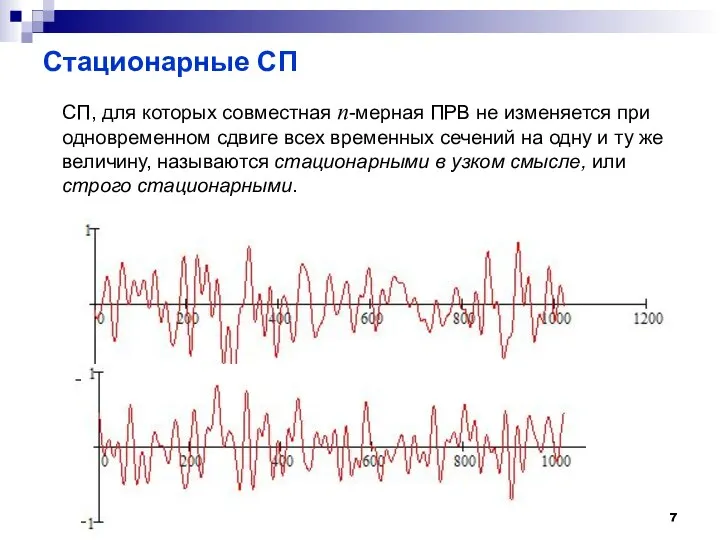
Стационарные СП
СП, для которых совместная n-мерная ПРВ не изменяется при одновременном сдвиге всех временных сечений на одну и ту же величину, называются стационарными в узком смысле, или строго стационарными.

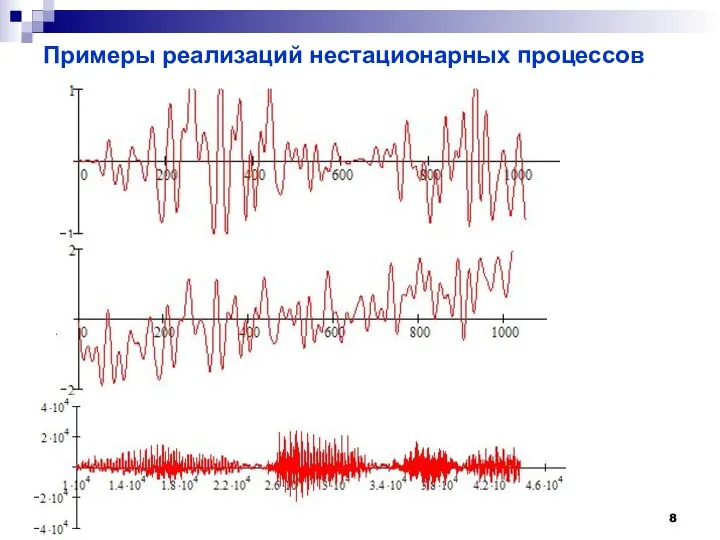
Примеры реализаций нестационарных процессов

Стационарные в широком смысле СП
СП называется стационарным в широком смысле, если при одновременном сдвиге сечений не изменяются лишь его моменты не выше второго порядка.
Заметим, что
(второй центральный момент) откуда следует постоянство дисперсии
СП, стационарный в узком смысле, стационарен и в широком смысле.
Обратное в общем случае неверно!

Обратный пример (частный случай)
− определитель квадратной матрицы, составленной из попарных коэффициентов корреляции отсчетов
− алгебраическое дополнение элемента

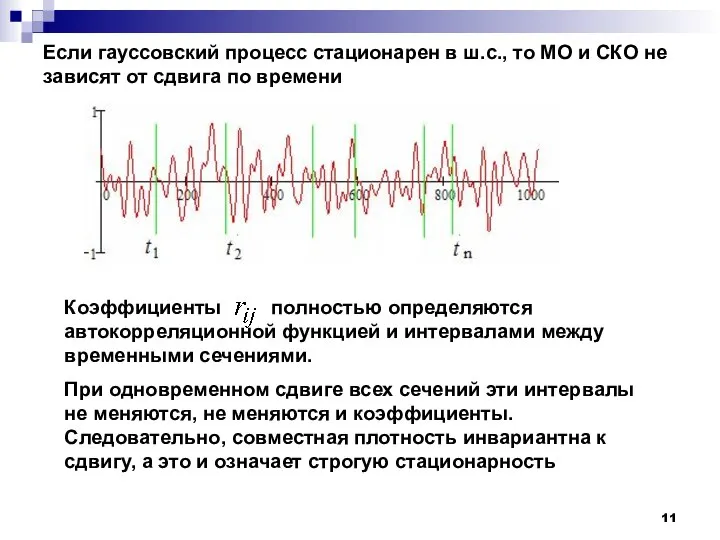
Коэффициенты полностью определяются автокорреляционной функцией и интервалами между временными сечениями.
При одновременном сдвиге всех сечений эти интервалы не меняются, не меняются и коэффициенты. Следовательно, совместная плотность инвариантна к сдвигу, а это и означает строгую стационарность
Если гауссовский процесс стационарен в ш.с., то МО и СКО не зависят от сдвига по времени

Эргодические случайные процессы
Для эргодических процессов моменты, найденные усреднением по ансамблю, равны соответствующим моментам, найденным усреднением по времени
В частности

АКФ
Эргодичность означает, по существу, то, что эта единственная реализация является полноправным представителем всего ансамбля
Достаточные условия эргодичности стационарного СП
Обычно наблюдателю доступна лишь одна (хотя, возможно, достаточно длинная) реализация случайного процесса.

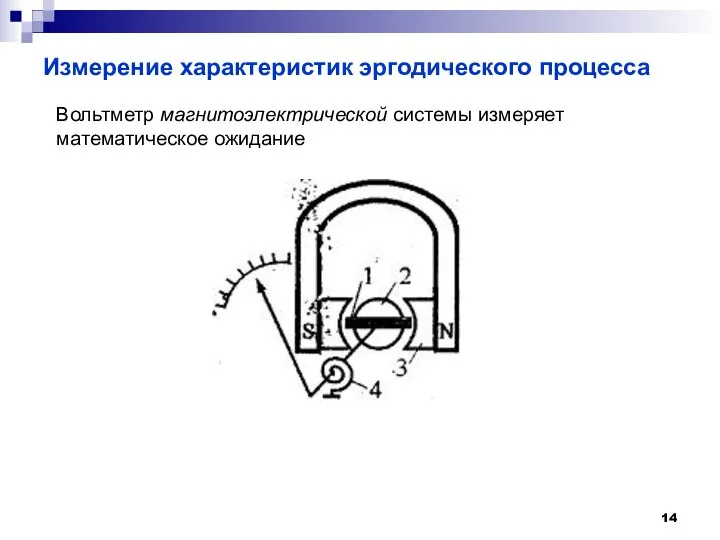
Измерение характеристик эргодического процесса
Вольтметр магнитоэлектрической системы измеряет математическое ожидание

Измерение характеристик эргодического процесса
Вольтметр электромагнитной или термоэлектрической системы, подключенный через разделительную емкость (для исключения постоянной составляющей) – измеряет среднеквадратическое значение (СКО)