Статистические сравнения

Цель – выяснить, имеются ли различия средних арифметических (одинаковых размерностей) по двум случайным выборкам.
Задачи:
1. Выявить, надёжно ли исходные случайные выборки представляют статистическое различие средних арифметических;
2. Определить, имеет ли существенное практическое значение степень установленного различия.

Необходимо решить основную задачу – надёжно ли исходные выборочные данные представляют различие средних, т.е. нужно установить, принадлежат ли обе группы к одной генеральной совокупности или к разным (по данному показателю).

План работы:
1. Определение средней арифметической величины - функция «AVERAGE» (OpenOffice.orgCalc), функция «СРЗНАЧ» (Microsoft Excel)
2. Определение стандартного (среднего квадратического) отклонения - функция «STDEV» (OpenOffice.orgCalc), функция «СТАНДОТКЛОН» (Microsoft Excel)
3. Определение значения квадратного корня из числа n (объем выборки) - функция «SQRT» (OpenOffice.orgCalc), функция «КОРЕНЬ» (Microsoft Excel)

4. Ошибка репрезентативности
Ошибка репрезентативности (m) – это стандартная мера возможного отклонения выборочного параметра от параметра генеральной совокупности.
Ошибка репрезентативности (представительности), или статистическая ошибка (m) – своей величиной показывает, насколько выборочные данные измерений ошибочно представляют, в среднем, отклонение рассчитанное по ним параметра (показателя) от истинного значения на генеральной совокупности данных.

Ошибка репрезентативности для средней арифметической величины m= δ / Vn ,
где δ - истинное стандартное отклонение,
n - объём выборки

Статистические ошибки – это не ошибки, допущенные при измерении. Они возникают исключительно во время отбора вариант из генеральной совокупности и к ошибкам измерений отношения не имеют. Единственная причина возникновения ошибки репрезентативности – не сплошной, а выборочный характер исследования (n # N), и единственный способ уменьшения ошибки – увеличение объёма выборки.

5. ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ И УРОВЕНЬ ЗНАЧИМОСТИ
Доверительная вероятность (Рдов) – вероятность, достаточная для суждения о генеральных параметрах на основании выборочных показателей.

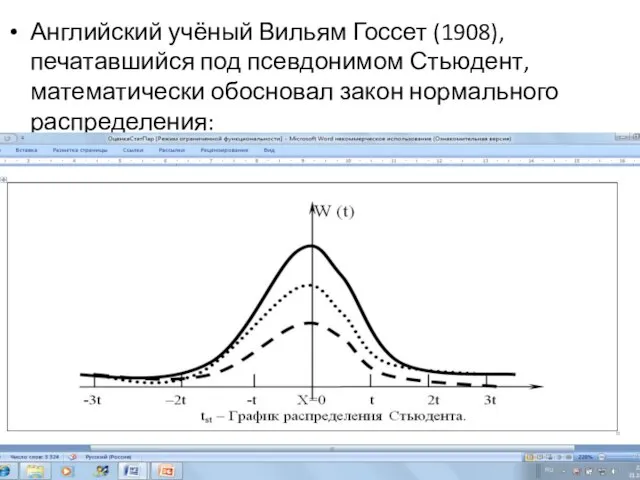
Английский учёный Вильям Госсет (1908), печатавшийся под псевдонимом Стьюдент, математически обосновал закон нормального распределения:

Обычно в качестве доверительных используют следующие уровни вероятности:
Р1 = 0,95; Р2 = 0,99; Р3 = 0,999.
В этом случае используются следующие уровни значимости («альфа»):
Ро = 0,05; Ро = 0,01; Ро = 0,001.
Это значит, что при оценивании генеральных параметров по выборочным характеристикам мы рискуем ошибиться в первом случае один раз на 20 испытаний, во втором случае – дин раз на 100 испытаний, в третьем случае – на 1000 испытаний.

Смысл доверительной вероятности (P дов.) – своей величиной показывает степень надёжности оценки статистического параметра.
Смысл уровня значимости (Ро) – своей величиной показывает степень ненадёжности оценки статистического параметра.

6. Доверительный интервал
Функция расчёта доверительного интервала – D: функция «CONFIDENCE» (OpenOffice.orgCalc), функция «ДОВЕРИТ» (Microsoft Excel)
Формула расчёта границ доверительного интервала :
хверхняя = х средняя + D,
хнижняя = х средняя - D,
где:
х верхняя – верхняя граница доверительного интервала,
х верхняя – верхняя граница доверительного интервала,
х средняя – выборочное среднее.

СМЫСЛ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА:
Доверительный интервал своими границами, с заданной доверительной вероятностью указывает, где находится истинное, генеральное, ожидаемое значение параметра.
Доверительный интервал указывает, с какой вероятностью (Рдов) и в каких пределах значений следует ожидать статистические параметры при повторных исследованиях на других случайных выборках.

СВОЙСТВА ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ
Размеры доверительных интервалов зависят от уровня доверительной вероятности (чем больше Рдов, тем больше величина доверительного интервала).
Чем больше n – объем выборки, или число измерений, тем меньше ошибка репрезентативности, тем меньше величина доверительного интервала.

7. Статистический вывод
Если установлено, что границы доверительных интервалов для ожидаемых средних не пересекаются, то говорят, что с заданной доверительной вероятностью (Рдов) установлено надёжное статистическое различие средних. Значит, исходные выборочные данные надёжно (достоверно) представили различия между средними арифметическими величинами.

Если доверительные интервалы пересекаются, т. е. имеются одинаковые ожидаемые значения средних, то говорят, что исходные выборочные данные ненадёжно представили различия между средними. Это не означает, что между х1 серд и х2 сред нет различий, это значит, что нет надёжности и наши выборки не отразили их.