Слайд 2Эпиграфом нашего урока являются слова А. Эйнштейна:
“Весь наш предшествующий опыт
приводит

к убеждению,
что природа является осуществлением того,
что математически проще всего представить”.
Слайд 3Цели урока
Повторить свойства и график степенной функции;
закрепить навыки построения графиков

и их описания с использованием программы «Живая геометрия»;
продолжить работу над умением анализировать поставленную задачу, предполагаемый результат и обобщать;
Воспитывать чувство взаимовыручки, коллективизма.
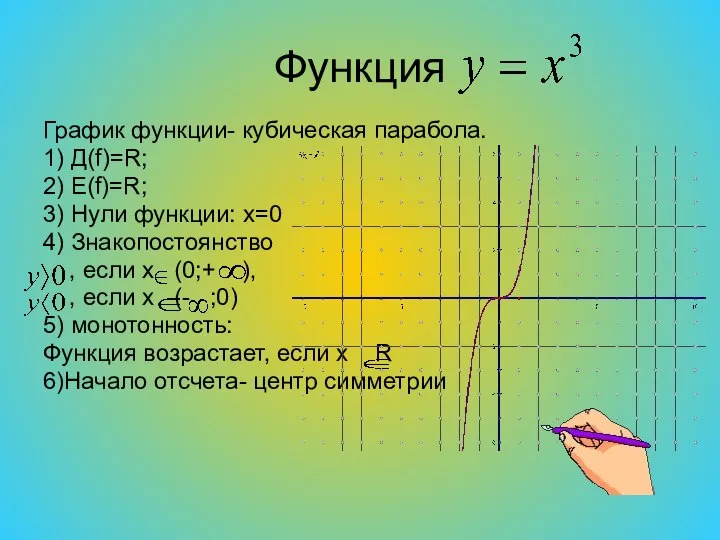
Слайд 4Функция
График функции- кубическая парабола.
1) Д(f)=R;
2) E(f)=R;
3) Нули функции: x=0
4) Знакопостоянство
,
если x (0;+ ),
, если x (- ;0)
5) монотонность:
Функция возрастает, если x R
6)Начало отсчета- центр симметрии
Слайд 5Число a- отвечает за перемещение вдоль оси ОХ;
если а 0,
то влево

на а единиц от 0;
если а 0,
то вправо на а единиц от 0.
Число b-отвечает за перемещение вдоль оси OY;
если b 0,
то вверх на b единиц от 0 ;
если b 0,
то вниз на b единиц от 0.
Слайд 6Функция
График функции- гипербола.
1) Д(y)=R, кроме х=0
2) E(y)=R, кроме y=0
3) Нули
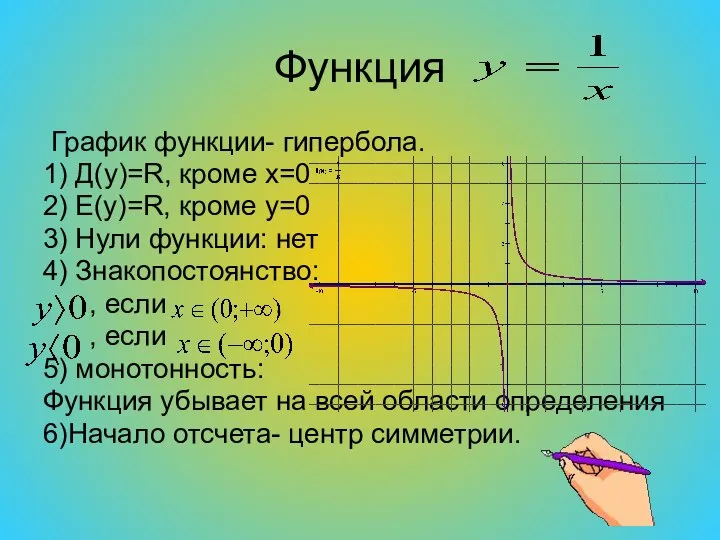
функции: нет
4) Знакопостоянство:
, если ,
, если
5) монотонность:
Функция убывает на всей области определения
6)Начало отсчета- центр симметрии.
Слайд 7Число а- отвечает за перемещение вдоль оси OX;
если ,
то влево на

a единиц от 0;
если ,
то вправо на а единиц от 0.
Число b- отвечает за перемещение вдоль оси OY;
если ,
то вверх на b единиц от 0;
если ,
то вниз на b единиц от 0.
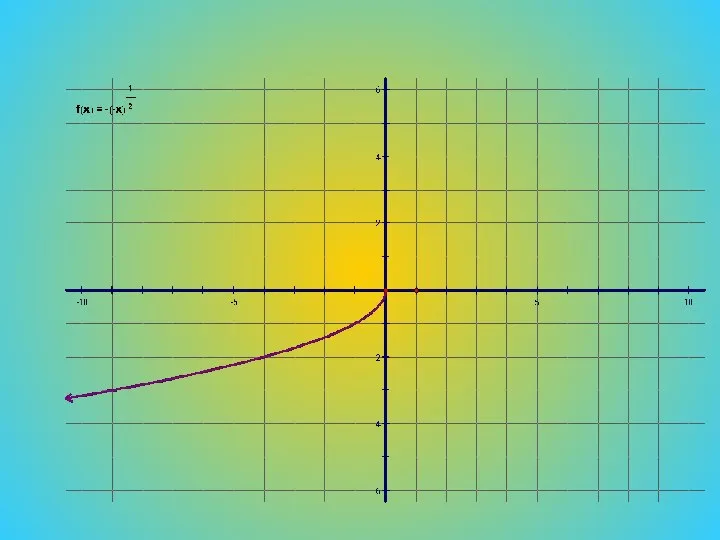
Слайд 8Функция
1) Д(y)=
2)E(y)=
3) Нули функции x=0
4) Знакопостоянство: ,
если
5)

монотонность:
Функция возрастает,
если
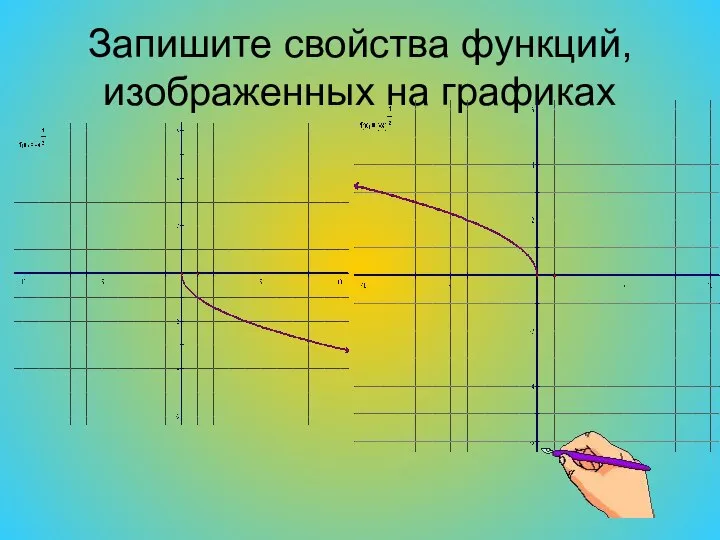
Слайд 9Запишите свойства функций, изображенных на графиках
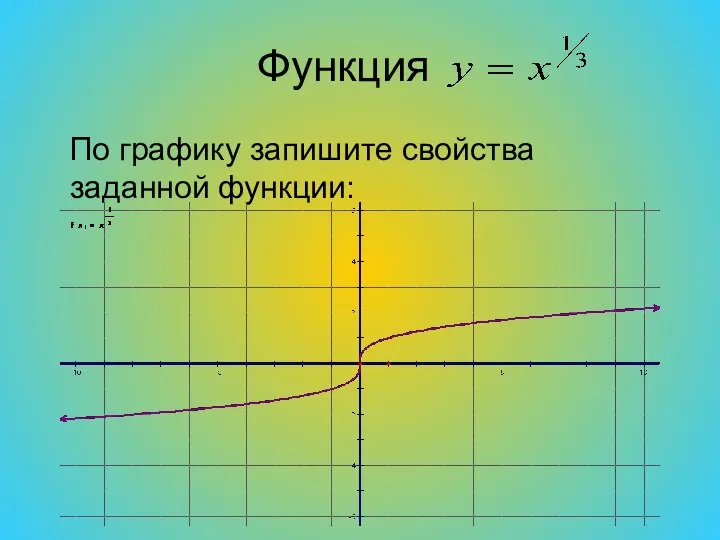
Слайд 11Функция
По графику запишите свойства заданной функции:
Слайд 12Постройте графики заданных функций

Слайд 13Итог урока:
Построение графика какой функции мы сегодня с вами повторили?
Испытывали

ли вы трудности в построении графиков и описания их?
Были ли восполнены пробелы в ваших знаниях?











 Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Презентация на тему Повторяем таблицу умножения
Презентация на тему Повторяем таблицу умножения  Дробные рациональные уравнения. Задания для интерактивной доски. 8 класс
Дробные рациональные уравнения. Задания для интерактивной доски. 8 класс Презентация на тему Проценты
Презентация на тему Проценты  Математическая викторина. 1 тур. Занимательные задачи
Математическая викторина. 1 тур. Занимательные задачи Римские цифры
Римские цифры Презентация на тему Аксиома параллельных прямых
Презентация на тему Аксиома параллельных прямых  Среднее арифметическое
Среднее арифметическое Прямоугольный параллелепипед
Прямоугольный параллелепипед Треугольник. Задачи по готовым чертежам (7 класс)
Треугольник. Задачи по готовым чертежам (7 класс) Геометрический и физический смысл производной
Геометрический и физический смысл производной Тест. Реши. И ты станешь уважать себя
Тест. Реши. И ты станешь уважать себя Эварист Галуа
Эварист Галуа ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА
ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА Равнобедренный треугольник и его свойства, 7 класс
Равнобедренный треугольник и его свойства, 7 класс Презентация на тему Параллелограмм и трапеция (8 класс)
Презентация на тему Параллелограмм и трапеция (8 класс)  Шкалы и координаты
Шкалы и координаты Подобные треугольники
Подобные треугольники Делители и кратные
Делители и кратные Работа по введению и усвоению определений или Семь вопросов Квинтилиана
Работа по введению и усвоению определений или Семь вопросов Квинтилиана Многоугольники в окружающем нас мире
Многоугольники в окружающем нас мире Повторение. Свойства умножения. Свойства деления
Повторение. Свойства умножения. Свойства деления Комплeксные числа. Арифметические операции над ними (10 класс)
Комплeксные числа. Арифметические операции над ними (10 класс) Метод типологии
Метод типологии Схема Горнера
Схема Горнера Решение задач по геометрии
Решение задач по геометрии Четные и нечетные функции. 10 класс
Четные и нечетные функции. 10 класс Алгебра логики
Алгебра логики