Содержание
- 2. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ И ГЕОМЕТРИИ ВЫПУКЛЫХ МНОЖЕСТВ Определение 1.3. Точка множества называется внутренней, если существует окрестность
- 3. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ И ГЕОМЕТРИИ ВЫПУКЛЫХ МНОЖЕСТВ Определение 1.6. Точка множества называется угловой или крайней, если
- 4. ОПРЕДЕЛЕНИЕ ВЫПУКЛОГО МНОГОГРАННИКА Определение 1.8. Выпуклое замкнутое множество точек пространства (плоскости), имеющее конечное число угловых точек,
- 5. ОПРЕДЕЛЕНИЕ БАЗИСНОГО РЕШЕНИЯ Определение 1.9. Любые m переменных системы n линейных уравнений 1.18 называются базисными, если
- 6. РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ ГРАФИЧЕСКИ Рассмотрим графическое решение системы m линейных неравенств:
- 7. Задача 1.4. Изобразить графически множество неотрицательных решений системы неравенств и определить координаты угловых точек области допустимых
- 8. РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ ГРАФИЧЕСКИ
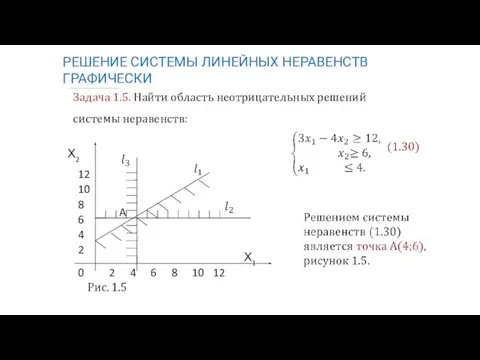
- 9. Задача 1.5. Найти область неотрицательных решений системы неравенств: РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ ГРАФИЧЕСКИ
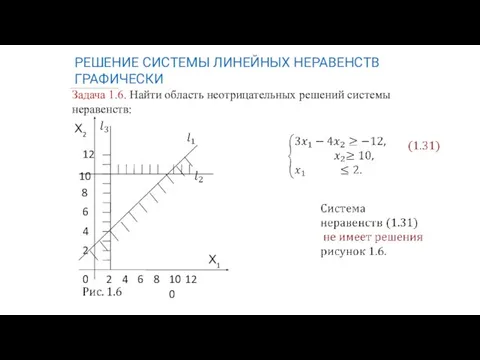
- 10. Задача 1.6. Найти область неотрицательных решений системы неравенств: РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ ГРАФИЧЕСКИ
- 11. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Определение 2.1. Решение задачи ЛП называется допустимым, если оно содержится в области
- 12. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЛП Теорема 2.1. Если в задаче ЛП допустимое множество не пусто и целевая функция
- 13. ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
- 14. ВЕКТОР ГРАДИЕНТ. СЛУЧАЙ АЛЬТЕРНАТИВНОГО РЕШЕНИЯ Определение 2.4. Вектор, координаты которого являются частными производными функции F(x) по
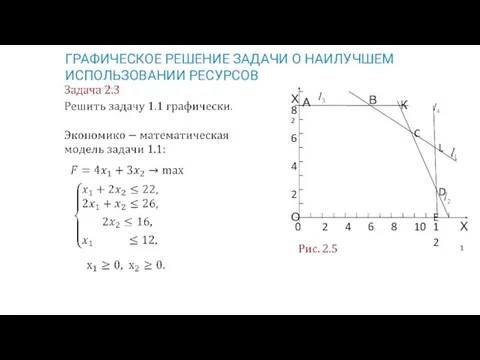
- 15. ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ О НАИЛУЧШЕМ ИСПОЛЬЗОВАНИИ РЕСУРСОВ
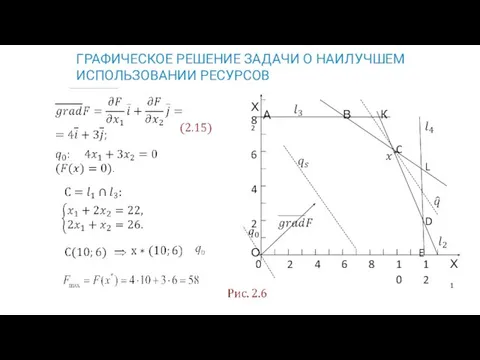
- 16. ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ О НАИЛУЧШЕМ ИСПОЛЬЗОВАНИИ РЕСУРСОВ :
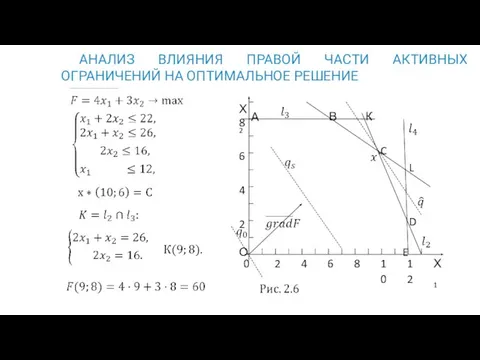
- 17. АНАЛИЗ ВЛИЯНИЯ ПРАВОЙ ЧАСТИ АКТИВНЫХ ОГРАНИЧЕНИЙ НА ОПТИМАЛЬНОЕ РЕШЕНИЕ :
- 18. АНАЛИЗ МОДЕЛЕЙ НА ЧУВСТВИТЕЛЬНОСТЬ. В рамках анализа модели на чувствительность выявляется чувствительность оптимального решения к определенным
- 20. Скачать презентацию












 Презентация по математике "Ломаные числа" -
Презентация по математике "Ломаные числа" -  Умножение числа 0 и на число 0 Умножение числа 1 и на число 1
Умножение числа 0 и на число 0 Умножение числа 1 и на число 1 Методы корреляционно-регрессионного анализа фондового рынка
Методы корреляционно-регрессионного анализа фондового рынка Статистическая проверка статистических гипотез
Статистическая проверка статистических гипотез Математика и техника. Их связь и значение
Математика и техника. Их связь и значение Групповое задание
Групповое задание Коррекция нелинейных систем
Коррекция нелинейных систем Перемещение тела на плоскости (задача)
Перемещение тела на плоскости (задача) Теорема Пифагора
Теорема Пифагора Таблица умножения на 2
Таблица умножения на 2 Повторение и закрепление. Итоговое повторение за год. 4 класс
Повторение и закрепление. Итоговое повторение за год. 4 класс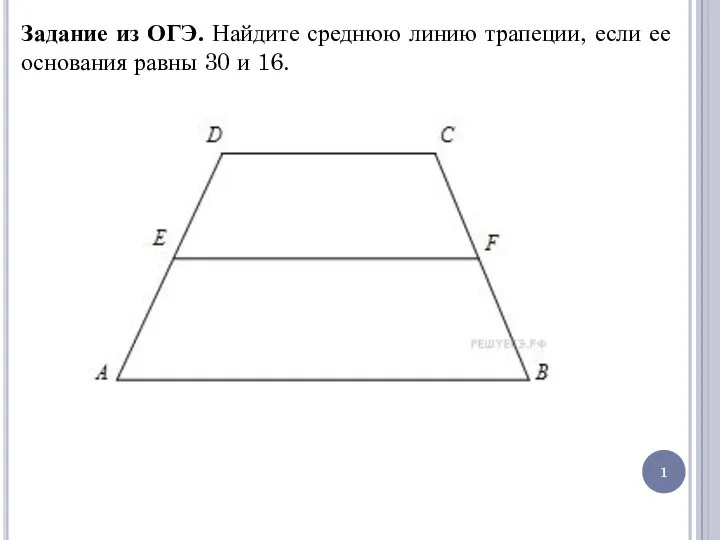 Прямоугольник. Ромб. Квадрат
Прямоугольник. Ромб. Квадрат Что такое разложение на множители и зачем оно нужно
Что такое разложение на множители и зачем оно нужно Гомотетия. Подобие фигур
Гомотетия. Подобие фигур Элементы математической логики
Элементы математической логики История возникновения науки геометрии
История возникновения науки геометрии Презентация на тему Окружность ее центр и радиус
Презентация на тему Окружность ее центр и радиус 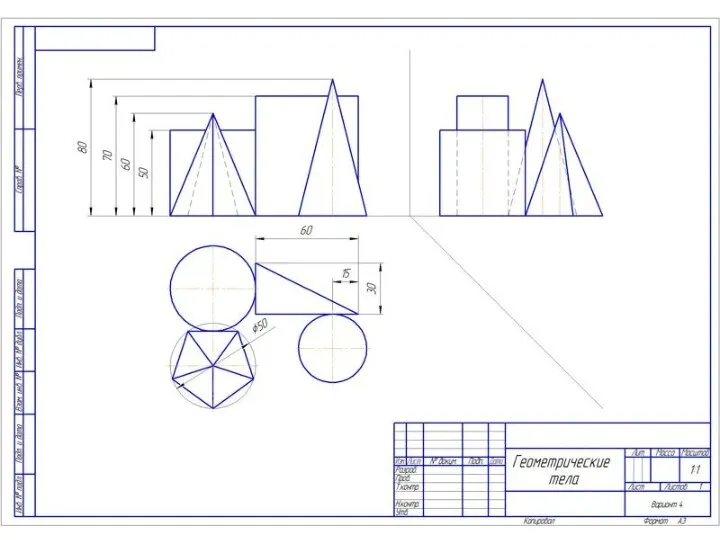 Геометрические тела. 9 класс
Геометрические тела. 9 класс Формирование регулятивных УУД у младших школьников при изучении геометрического материала
Формирование регулятивных УУД у младших школьников при изучении геометрического материала Стандартизация в различных сферах. Сущность стандартизации
Стандартизация в различных сферах. Сущность стандартизации Без знаний дробей никто не может признаваться знающим арифметику
Без знаний дробей никто не может признаваться знающим арифметику Признак перпендикулярности плоскостей
Признак перпендикулярности плоскостей Kоординатная плоскость
Kоординатная плоскость Средние величины
Средние величины Математика. Роль математики в жизни людей и общества
Математика. Роль математики в жизни людей и общества Действия с натуральными числами. Сложение и вычитание
Действия с натуральными числами. Сложение и вычитание Решение уравнений
Решение уравнений Презентация на тему Римские цифры (3 класс)
Презентация на тему Римские цифры (3 класс)