Слайд 2ПЛОЩАДЬ ФИГУРЫ
Для нахождения площади фигуры, ограниченной кривыми, используется определенный интеграл. При этом,

пределы интегрирования находятся в точках пересечения заданных кривых
Слайд 3РАБОТА В MATHCAD
В среде Mathcad для определения пределов интегрирования используется функция root(f(x),x),

а для нахождения определенного интеграла – соответствующий шаблон на наборной панели Calculus
Слайд 4ФОРМУЛИРОВКА ЗАДАНИЯ
Найти площадь фигуры, ограниченной кривыми:

Слайд 5РЕАЛИЗАЦИЯ В СРЕДЕ MATHCAD
Для определения пределов интегрирования необходимо будет построить графики обеих

функций, графически определить приближенные значения, а потом, используя функцию root(f(x),x), найти точные значения пределов интегрирования
Для построения графиков функций, обозначим одну функцию за f(x), а вторую за y(x)
Слайд 6РЕАЛИЗАЦИЯ В СРЕДЕ MATHCAD
Зададим обе функции:

Слайд 7РЕАЛИЗАЦИЯ В СРЕДЕ MATHCAD
Построим графики этих функций:
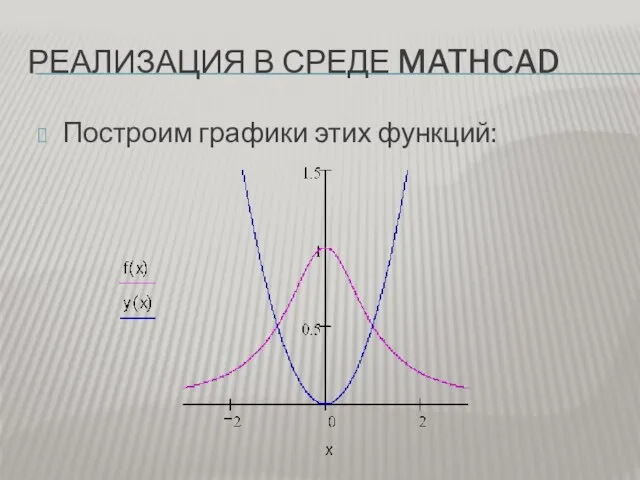
Слайд 8РЕАЛИЗАЦИЯ В СРЕДЕ MATHCAD
По графику определилась фигура, площадь которой нужно найти:
Зададим эту

новую функцию в Mathcad
Слайд 9РЕАЛИЗАЦИЯ В СРЕДЕ MATHCAD
Также графически определились приближенные пределы интегрирования
Зададим приближенное значение нижнего

предела интегрирования:
Слайд 10РЕАЛИЗАЦИЯ В СРЕДЕ MATHCAD
Точное значение нижнего предела интегрирования найдем с помощью функции

root.
Будем учитывать, что вместо f(x), в функции root используется g(x):
Слайд 11РЕАЛИЗАЦИЯ В СРЕДЕ MATHCAD
Зададим приближенное значение верхнего предела интегрирования и найдем его

точное значение:
Слайд 12РЕАЛИЗАЦИЯ В СРЕДЕ MATHCAD
Теперь можно найти значение интеграла фигуры g(x), ограниченной линиями

f(x) и y(x):











 Модели и развёртки многогранников
Модели и развёртки многогранников Правильная пирамида
Правильная пирамида Треугольники. Треугольник в науке
Треугольники. Треугольник в науке Число и цифра 8
Число и цифра 8 Анализ геометрической формы предмета (7 класс)
Анализ геометрической формы предмета (7 класс) Выполни задания в электронном дневнике
Выполни задания в электронном дневнике Законы сложения
Законы сложения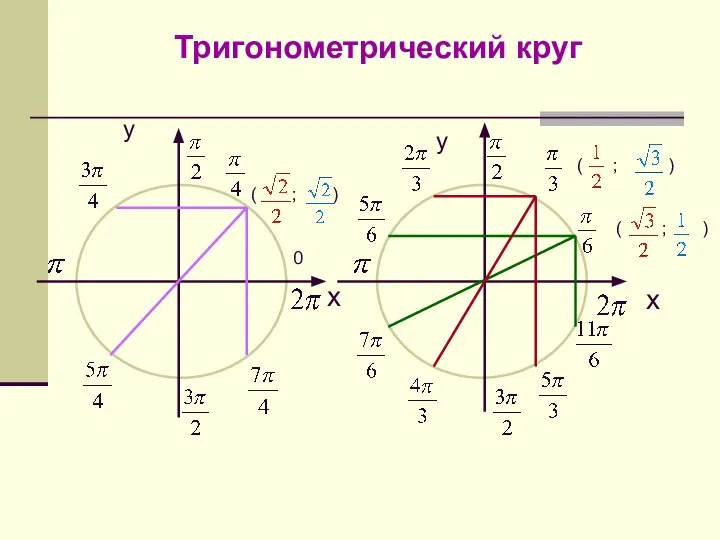 Тригонометрический круг
Тригонометрический круг Алгоритмы в нашей жизни
Алгоритмы в нашей жизни Презентация на тему Подготовка к ЕГЭ по математике
Презентация на тему Подготовка к ЕГЭ по математике  Числовые последовательности. Арифметическая прогрессия
Числовые последовательности. Арифметическая прогрессия Математические игры. 6 класс
Математические игры. 6 класс Функции многих переменных: частные производные, дифференциалы. Лекция 2
Функции многих переменных: частные производные, дифференциалы. Лекция 2 chislo-pi
chislo-pi Комбинаторные задачи
Комбинаторные задачи Линейные пространства и линейные операторы. Лекция 5
Линейные пространства и линейные операторы. Лекция 5 Презентация на тему Действия с целыми числами
Презентация на тему Действия с целыми числами  Дискретная математика. Множества
Дискретная математика. Множества Таблицы. Алгебра 7 класс
Таблицы. Алгебра 7 класс Планиметрия. Стереометрия
Планиметрия. Стереометрия Решение квадратных уравнений с параметром
Решение квадратных уравнений с параметром Решение задач на применение признаков параллельности прямых
Решение задач на применение признаков параллельности прямых Логические законы
Логические законы Решение систем неравенств (8 класс)
Решение систем неравенств (8 класс) Знаете ли вы... Высота, длина, вес
Знаете ли вы... Высота, длина, вес Занимательный устный счет
Занимательный устный счет Урок математики 13.09
Урок математики 13.09 Презентация на тему Страна отрицательных чисел
Презентация на тему Страна отрицательных чисел