Слайд 4Определение функции.
Функцией называется зависимость между двумя переменными (У и Х) в которой

каждому значению независимой переменной (Х) соответствует единственное значение зависимой переменной (У).
Независимую переменную называют - аргумент.
Значения зависимой переменной называют значениями функции.
Запись У=f (X) читается: У – функция от Х.
Слайд 5Способы задания функции.
Графически.
С помощью формулы.
Таблицей.
Словесный.
Рекуррентный.

Слайд 9Каждому натуральному числу поставим в соответствие его квадрат.

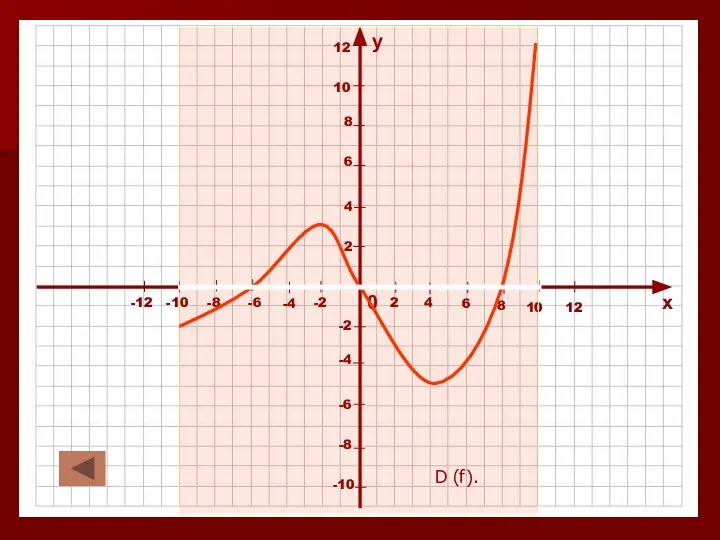
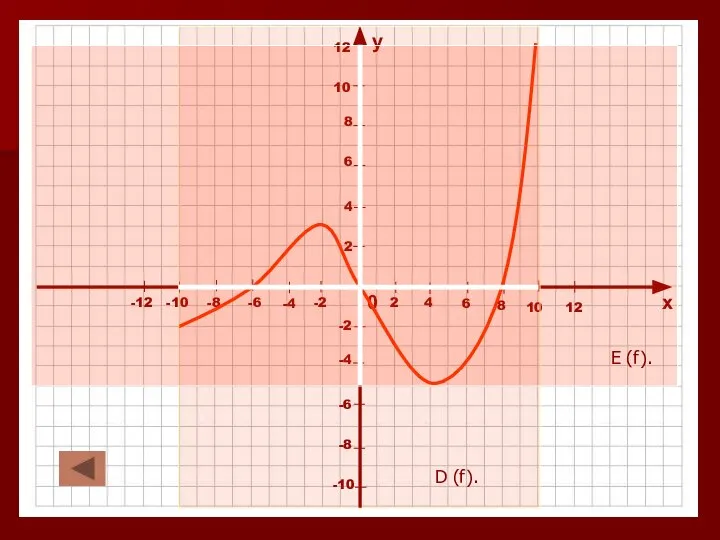
Слайд 11Область определения и множество значений функции.
Все значения независимой переменной образуют область определения

функции -D (f).
Все значения, которые принимает зависимая переменная, образуют область значений функции – E (f).
Слайд 15 Если функция задана формулой и не указана ее область определения, то

считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл.
Укажите область определения функций:
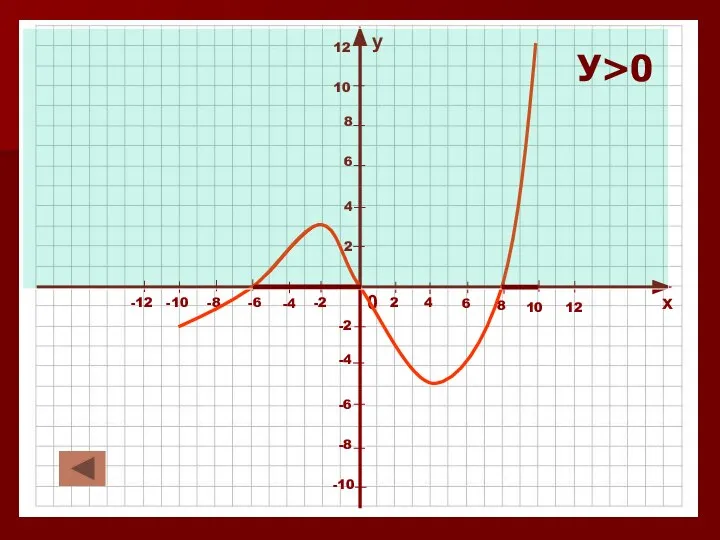
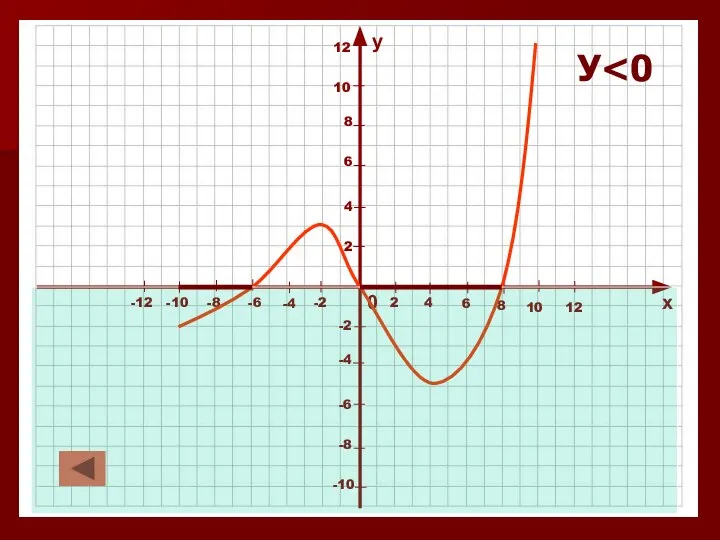
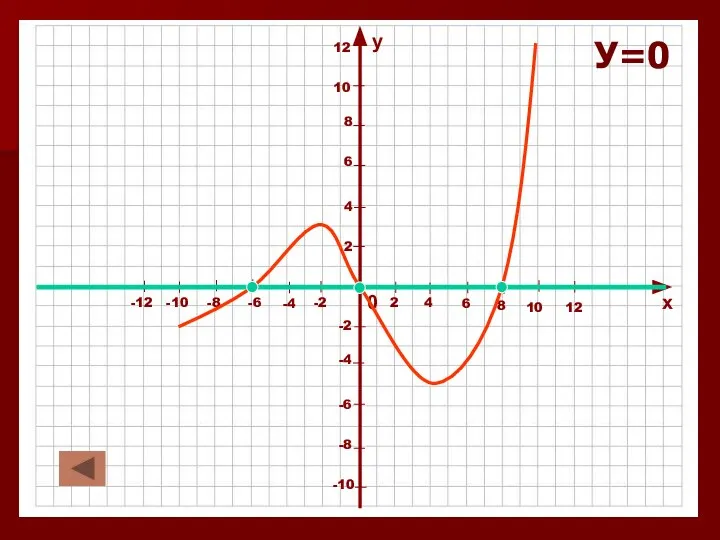
Слайд 16Промежутки знакопостоянства и нули функции.
1. Значения функции положительны. У>0
2. Значения функции отрицательны.

У<0
3. Значения функции равны нулю. У=0
Слайд 20Монотонность функции.
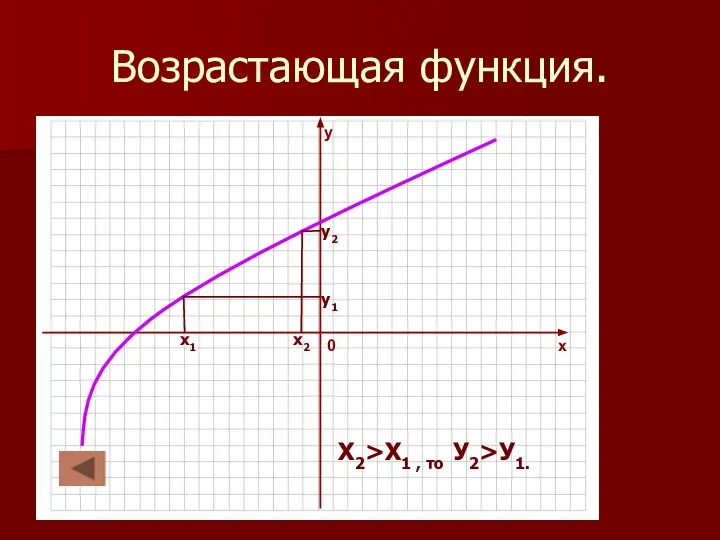
Функция называется возрастающей на некотором промежутке, если большему значению аргумента из

этого промежутка соответствует большее значение функции.
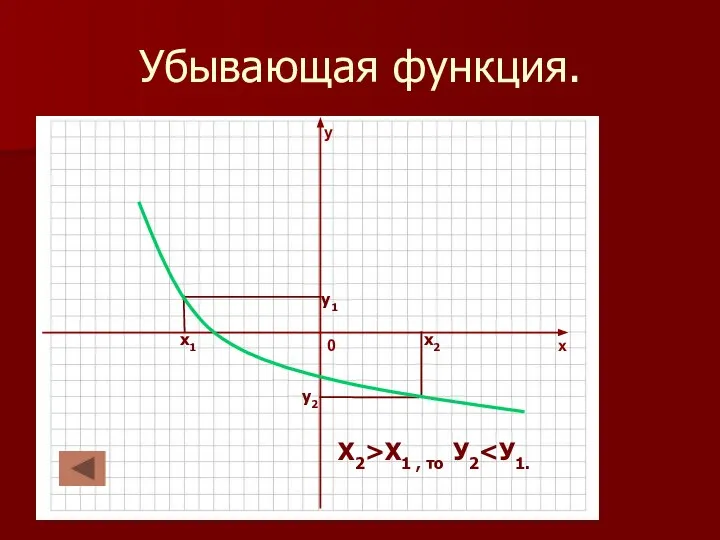
Функция называется убывающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Слайд 21Возрастающая функция.
х1
х2
у1
у2
Х2>Х1 , то У2>У1.
Слайд 22Убывающая функция.
х1
х2
у1
у2
Х2>Х1 , то У2<У1.
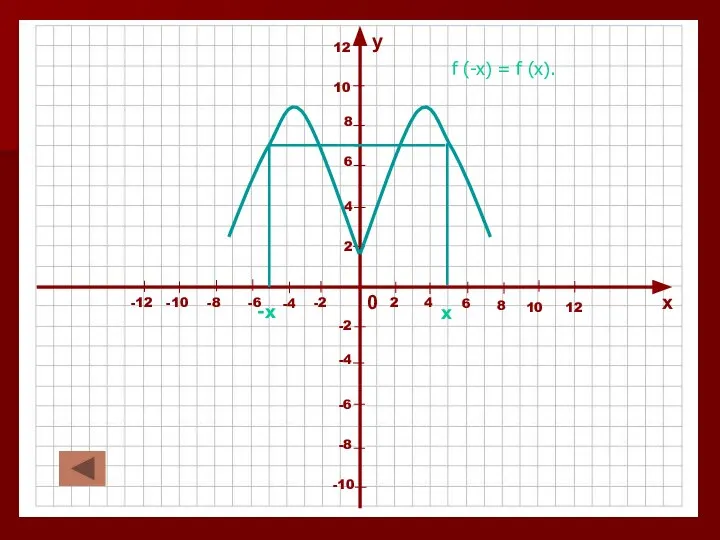
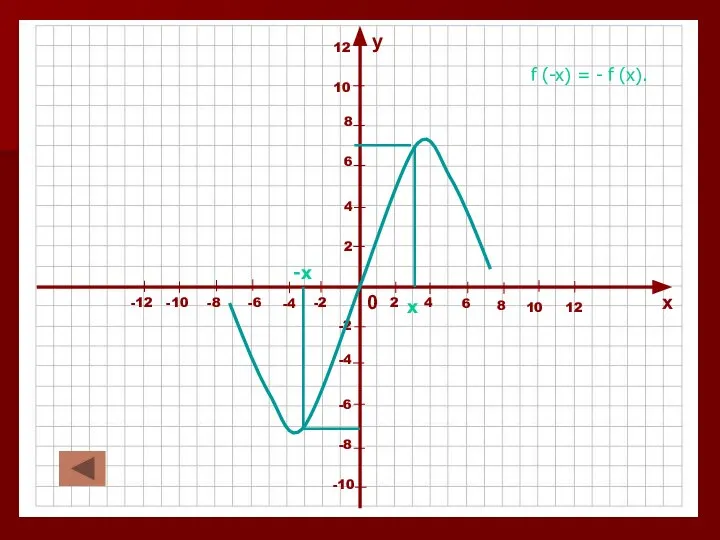
Слайд 24Четные и нечетные функции.
Функция у = f (x) называется четной, если для

всех х из области определения функции выполняется равенство f (-x) = f (x).
Функция у = f (x) называется нечетной, если для всех х из области определения функции выполняется равенство f (-x) = - f (x).
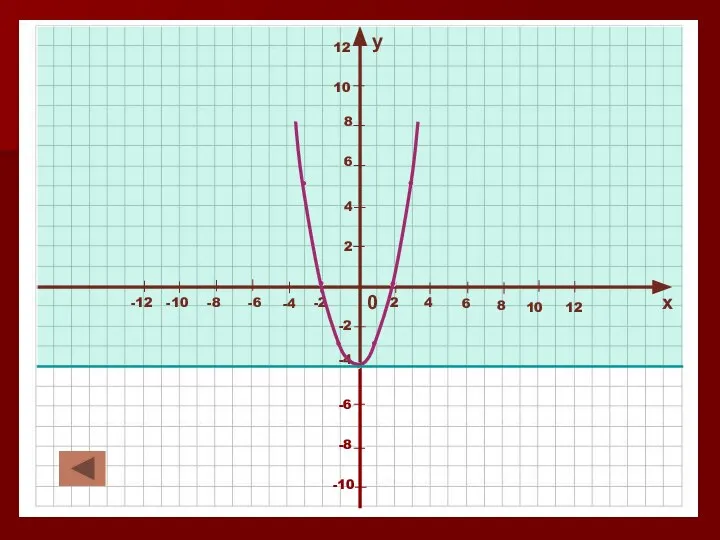
Слайд 27Ограниченность функции.
Функция y=f (x) называется ограниченной снизу, если для любого х из

области определения функции выполняется условие
f (x)>a, где а – некоторое число.
Функция y=f (x) называется ограниченной сверху, если для любого х из области определения функции выполняется условие
f (x)< a, где а – некоторое число.
Функция называется ограниченной, если она ограничена и снизу, и сверху.




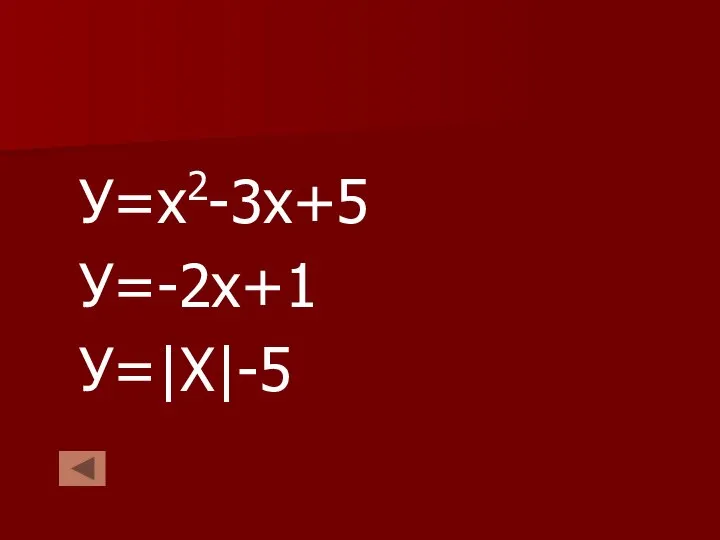














 Декартова система координат в евклидовом пространстве
Декартова система координат в евклидовом пространстве Ребусы. Алгебра
Ребусы. Алгебра Домашнее задание. Примеры и уравнения
Домашнее задание. Примеры и уравнения Алгебра. 7 класс
Алгебра. 7 класс Влияние математических действий на аликвоты
Влияние математических действий на аликвоты Преобразование буквенных выражений. Правила математического синтаксиса
Преобразование буквенных выражений. Правила математического синтаксиса Владимир Модестович Брадис и его замечательные таблицы
Владимир Модестович Брадис и его замечательные таблицы Смеси и сплавы в задачах №13 ЕГЭ-2015 г
Смеси и сплавы в задачах №13 ЕГЭ-2015 г Признаки равенства треугольников
Признаки равенства треугольников Методика изучения объема
Методика изучения объема Тела и поверхности вращения
Тела и поверхности вращения Презентация к уроку математики 6 класса учителя математики НОУ СОШ «Азъ Буки Веди» Ивахненко Натальи Геннадьевны
Презентация к уроку математики 6 класса учителя математики НОУ СОШ «Азъ Буки Веди» Ивахненко Натальи Геннадьевны Второй признак равенства треугольников
Второй признак равенства треугольников Линейное уравнение с двумя переменными
Линейное уравнение с двумя переменными Последовательности
Последовательности Логика и логические задачи
Логика и логические задачи Пирамида
Пирамида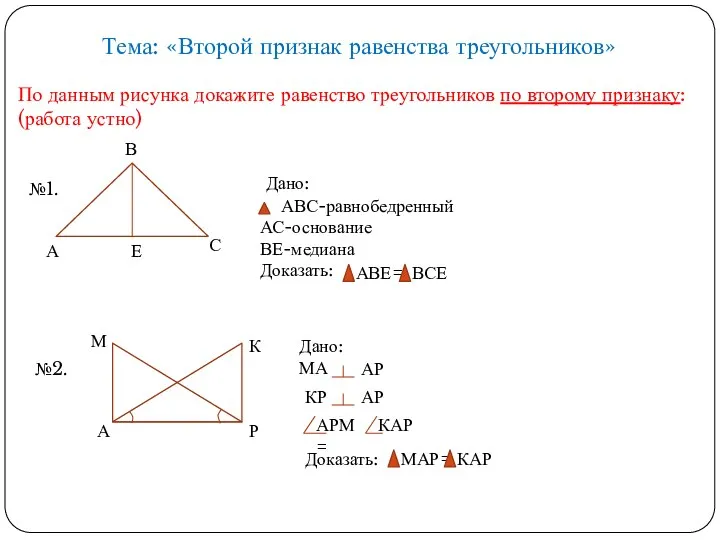 Равенство треугольников по второму признаку
Равенство треугольников по второму признаку 13_razn_dejstv_1
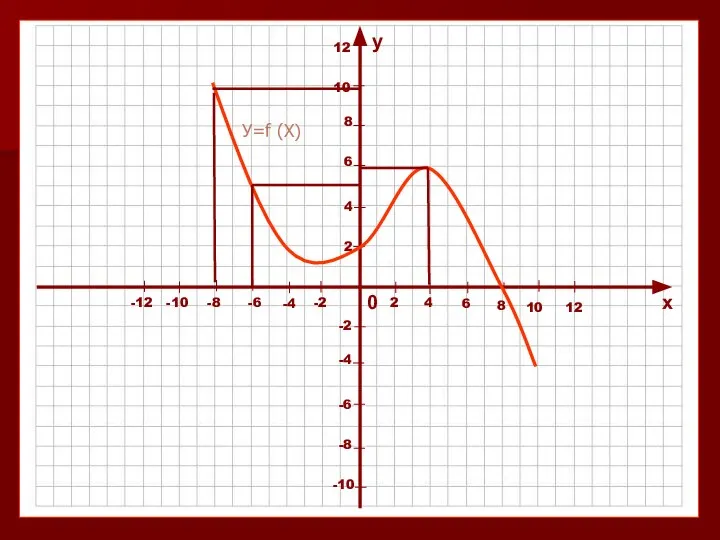
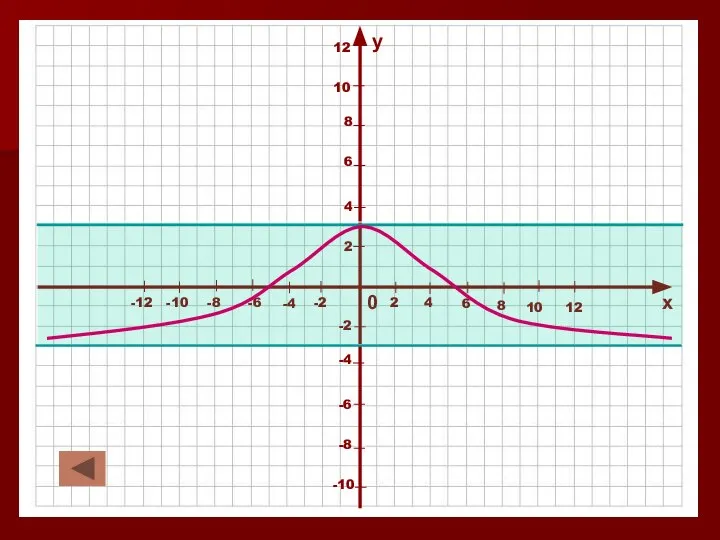
13_razn_dejstv_1 Какой функции соответствует график
Какой функции соответствует график Презентация на тему Решение иррациональных неравенств (11 класс)
Презентация на тему Решение иррациональных неравенств (11 класс)  Сходимость несобственных интегралов второго рода от неотрицательных функций
Сходимость несобственных интегралов второго рода от неотрицательных функций Решение нерапвенства
Решение нерапвенства ВКР: Исследование нормального строения конечных групп
ВКР: Исследование нормального строения конечных групп Деятельность как опора самости
Деятельность как опора самости Function as one of the fundamental concepts at secondary school mathematics
Function as one of the fundamental concepts at secondary school mathematics Презентация на тему Решение квадратных неравенств
Презентация на тему Решение квадратных неравенств 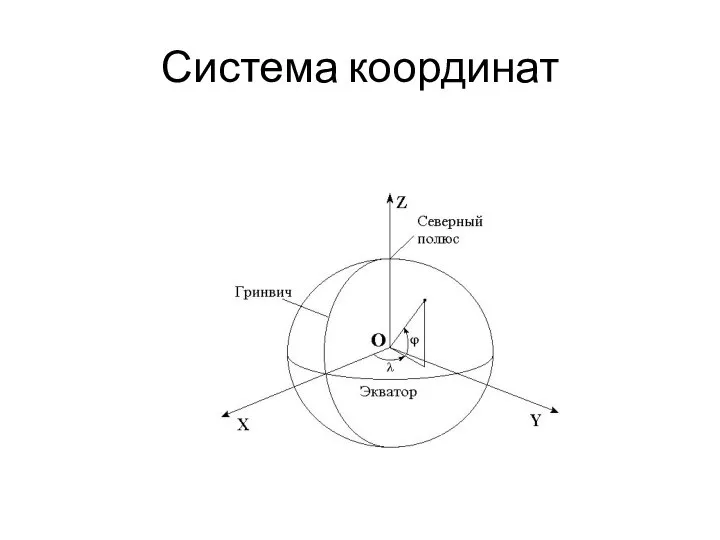 Система координат. Географические координаты
Система координат. Географические координаты