Свойства функций

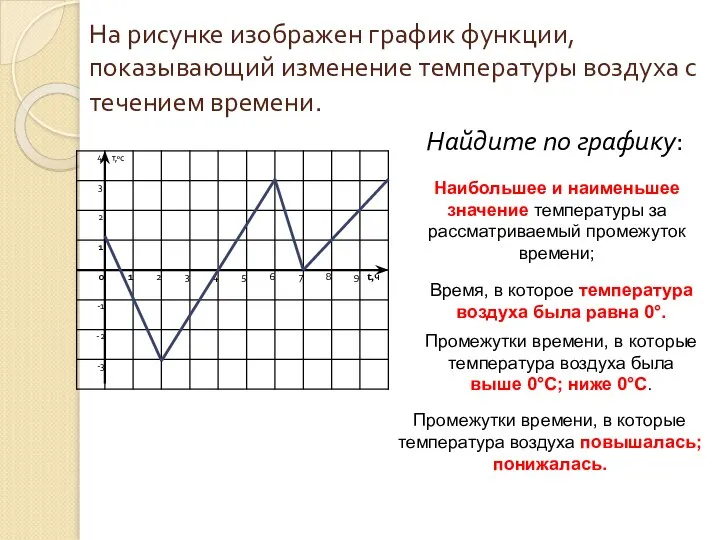
На рисунке изображен график функции, показывающий изменение температуры воздуха с течением времени.
Найдите по графику:
Наибольшее и наименьшее значение температуры за рассматриваемый промежуток времени;
Время, в которое температура воздуха была равна 0°.
Промежутки времени, в которые температура воздуха была выше 0°С; ниже 0°С.
Промежутки времени, в которые температура воздуха повышалась; понижалась.

Свойства функции
Область определения
Область значений
Наименьшее и наибольшее значение функции
Нули функции
Положительные значения функции(у >0) и отрицательные значения функции (у<0)
Промежутки монотонности: возрастание и убывание функции
далее

Область определения функции – все значения, которые может принимать аргумент.
Обозначение D(y)=[-5;5]
назад

Область значений функции – все значения,
которые может принимать функция.
Обозначение Е(y)=[-4;2]
назад

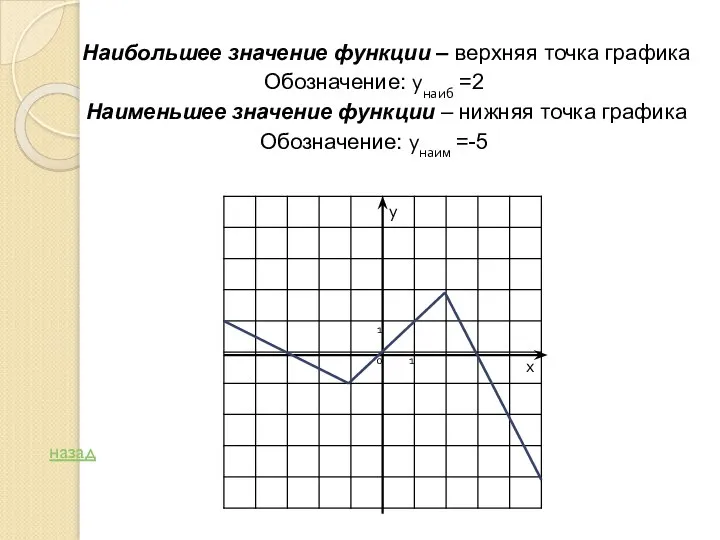
Наибольшее значение функции – верхняя точка графика
Обозначение: унаиб =2
Наименьшее значение функции – нижняя точка графика
Обозначение: унаим =-5
назад

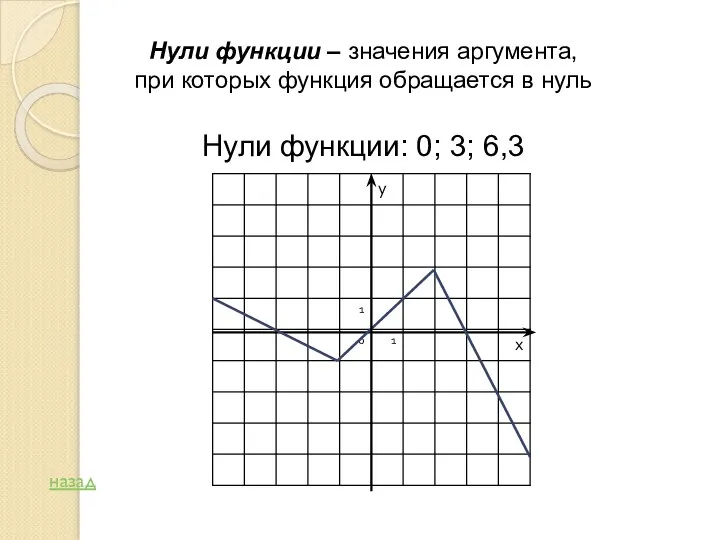
Нули функции – значения аргумента,
при которых функция обращается в нуль
Нули функции: 0; 3; 6,3
назад

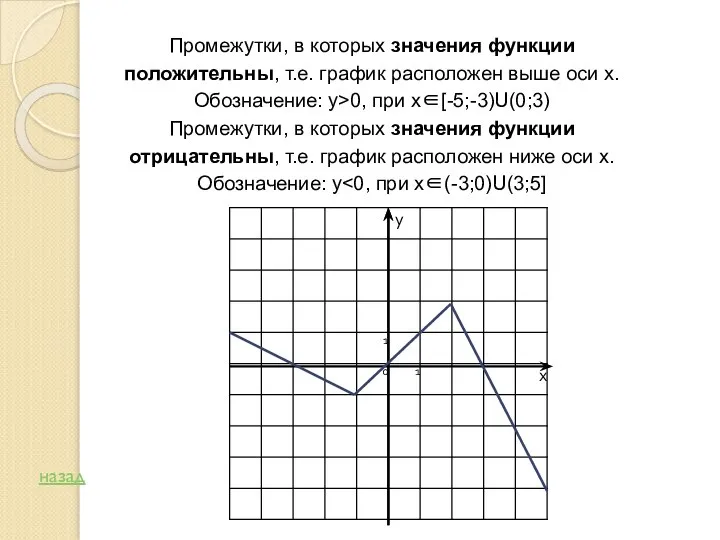
Промежутки, в которых значения функции
положительны, т.е. график расположен выше оси х.
Обозначение: у>0, при х∈[-5;-3)U(0;3)
Промежутки, в которых значения функции
отрицательны, т.е. график расположен ниже оси х.
Обозначение: у<0, при х∈(-3;0)U(3;5]
назад

Промежутки возрастания функции
Функция возрастает при х∈[-1;2]
Промежутки убывания функции
Функция убывает при х∈[-5;-1],[2;5]
назад

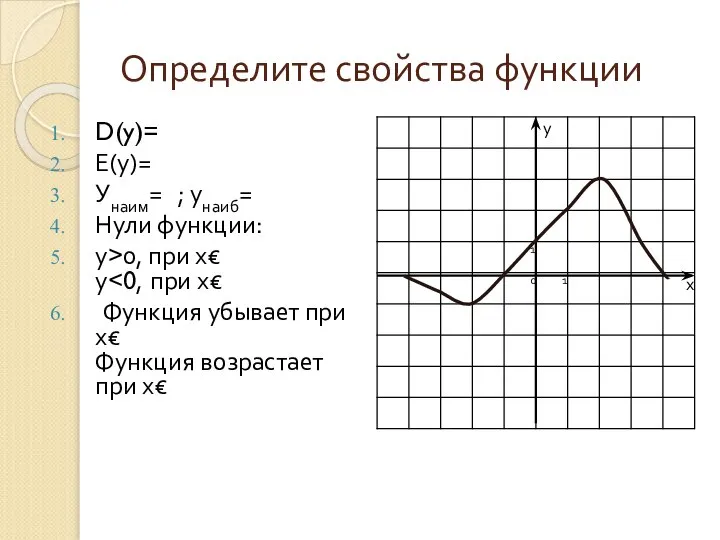
Определите свойства функции
D(y)=
Е(у)=
Унаим= ; унаиб=
Нули функции:
у>0, при х€
у<0, при х€
Функция убывает при х€
Функция возрастает при х€

Определите свойства функции
D(y)=[-4;4];
Е(у)=[-1;3];
Унаим=-1; унаиб=3;
Нули функции: -4, -1, 4;
у>0, при х€(-1;4];
у<0, при х€[-4;-1);
Функция убывает при х€[-4;-2],[2;4],
Функция возрастает при х€[-2;2].

Отчеты групп

Функция f(x) задана на промежутке [-5;5].
Группа 1

Функция f(x) задана на промежутке[-6;5].
Группа 2

Функция f(x) задана на промежутке[-4;5].
Группа 3

1 группа
Область определения функции – отрезок [-3; 4], наибольшее значение равно 5, наименьшее
равно -1.

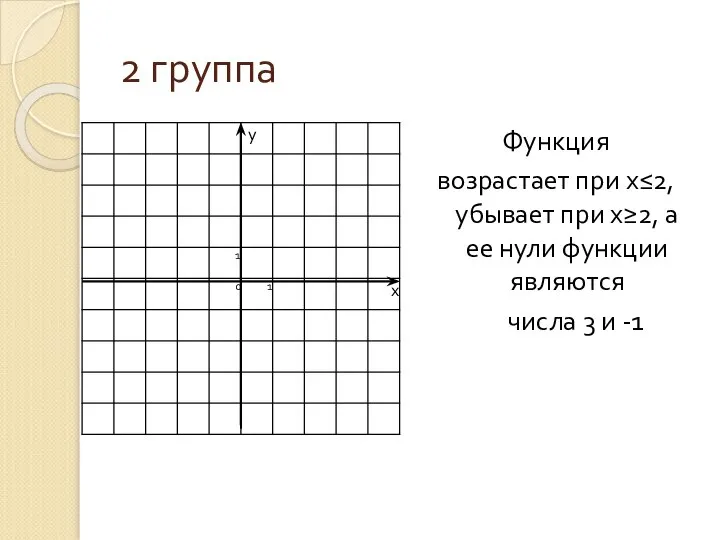
2 группа
Функция
возрастает при х≤2, убывает при х≥2, а ее нули функции являются
числа 3 и -1