- Главная
- Математика
- Понятие неравенство

Содержание
Слайд 2Понятие «неравенство» - одно из фундаментальных понятий школьного курса математики.
Цель
Понятие «неравенство» - одно из фундаментальных понятий школьного курса математики.
Цель

курса:
- развитие математических способностей: логически мыслить, умения
анализировать, обобщать, делать выводы через усвоение различных приёмов решения неравенств и систем неравенств;
- преодоление психологического барьера, связанного с новой формой проведения итоговой аттестации по математике, и обретение уверенности в своих силах.
- развитие математических способностей: логически мыслить, умения
анализировать, обобщать, делать выводы через усвоение различных приёмов решения неравенств и систем неравенств;
- преодоление психологического барьера, связанного с новой формой проведения итоговой аттестации по математике, и обретение уверенности в своих силах.
Умение решать неравенства различных видов позволяет обеспечить базовую подготовку школьника для успешного прохождения итоговой аттестации по математике за курс основной школы.
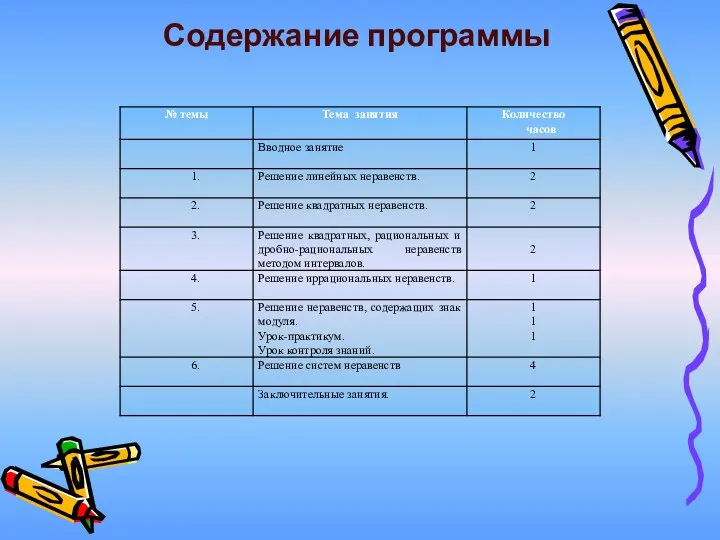
Слайд 3Содержание программы
Содержание программы
- Предыдущая
Конус. ОкружностьСледующая -
Система памяти ПК Тест Вписанные и описанные цилиндры
Тест Вписанные и описанные цилиндры Виды треугольников
Виды треугольников Решение неравенств с помощью систем
Решение неравенств с помощью систем Арккосинус. Решение уравнения cos t = a
Арккосинус. Решение уравнения cos t = a Способы задания плоскости
Способы задания плоскости Площадь криволинейной трапеции
Площадь криволинейной трапеции Начертательная геометрия
Начертательная геометрия Метод координат. Решение задач
Метод координат. Решение задач Веселая математика
Веселая математика Отображение. Отражение относительно прямой. Преобразование единичного квадрата
Отображение. Отражение относительно прямой. Преобразование единичного квадрата Десятичные дроби
Десятичные дроби Решение задач. 3 класс
Решение задач. 3 класс Учимся писать цифры
Учимся писать цифры Замощение плоскости правильными многоугольниками. 5 класс
Замощение плоскости правильными многоугольниками. 5 класс Пропорции и проценты
Пропорции и проценты Задачи для всех-всех-всех
Задачи для всех-всех-всех Многомерные случайные величины
Многомерные случайные величины Чирмешән муниципаль районы Лашман урта гомумбелем бирү мәктәбе
Чирмешән муниципаль районы Лашман урта гомумбелем бирү мәктәбе Решение задач с помощью систем уравнений второй степени
Решение задач с помощью систем уравнений второй степени График функции
График функции Формула полной вероятности и Байеса
Формула полной вероятности и Байеса Взаимное расположение прямых и плоскостей
Взаимное расположение прямых и плоскостей Презентация на тему Параллелепипед и его объем
Презентация на тему Параллелепипед и его объем  Приведение к каноническому виду уравнений параболического типа
Приведение к каноническому виду уравнений параболического типа Презентация на тему Метод координат в пространстве
Презентация на тему Метод координат в пространстве  Уравнение с двумя переменными
Уравнение с двумя переменными Таблица умножения на 2
Таблица умножения на 2 Подготовка к экзамену по математике
Подготовка к экзамену по математике