Содержание
- 2. Математическая статистика изучает математические методы систематизации, обработки и использования статистических данных для научных и производственных целей
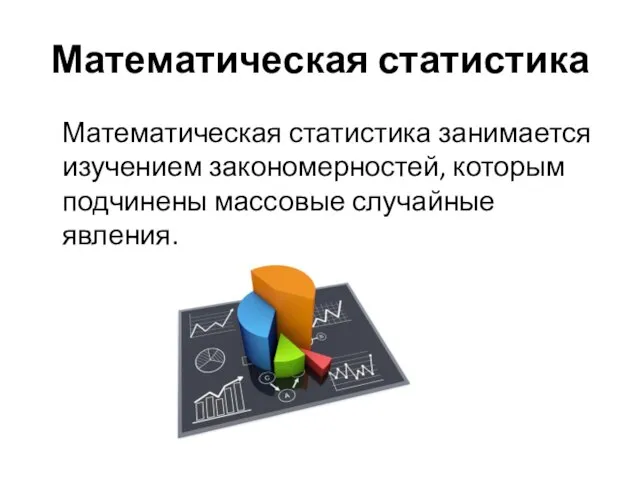
- 3. Математическая статистика Математическая статистика занимается изучением закономерностей, которым подчинены массовые случайные явления.
- 4. Случайная величина Случайная величина – это величина, значение которой зависит от случая. Случайные величины могут быть
- 5. Случайная величина Случайные величины могут быть дискретными т.е. принимать только конечное или счетное множество определенных значений
- 6. Числовые характеристики дискретных случайных величин
- 7. Математическое ожидание (среднее значение) Определение. Математическим ожиданием называется сумма произведений значения случайной величины на её вероятность:
- 8. Дисперсия случайной величины Определение. Дисперсией случайной величины х называется математическое ожидание квадрата отклонения значения величины от
- 9. Пусть требуется оценить совокупность однородных объектов относительно некоторого качественного или количественного признака. Вся совокупность объектов, подлежащих
- 10. Выборочной совокупностью (ВС), или просто выборкой, называют часть элементов ГС, отобранных для изучения требуемого признака. Объемом
- 11. Генеральная совокупность – совокупность всех исследуемых объектов Выборочная совокупность (выборка) – совокупность случайно отобранных объектов Случайный
- 12. Пример Из 10000 изделий для контроля отобрали 100 изделий. Объем генеральной совокупности равен 10000, объем выборки
- 13. Для статистической обработки результаты исследования объектов, составляющих выборку, представляют в виде числовой выборки (последовательность чисел). Разность
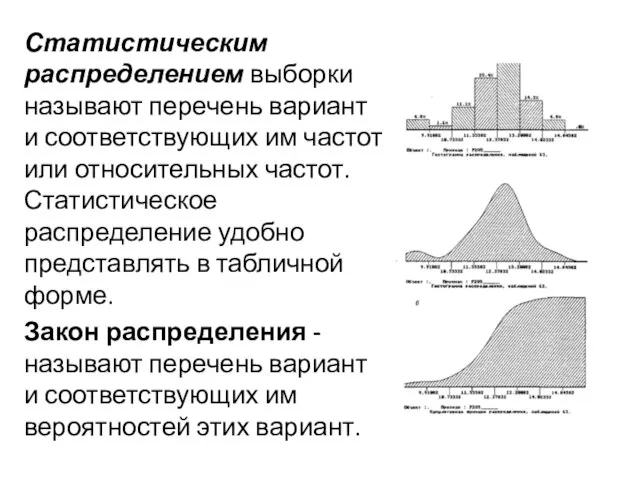
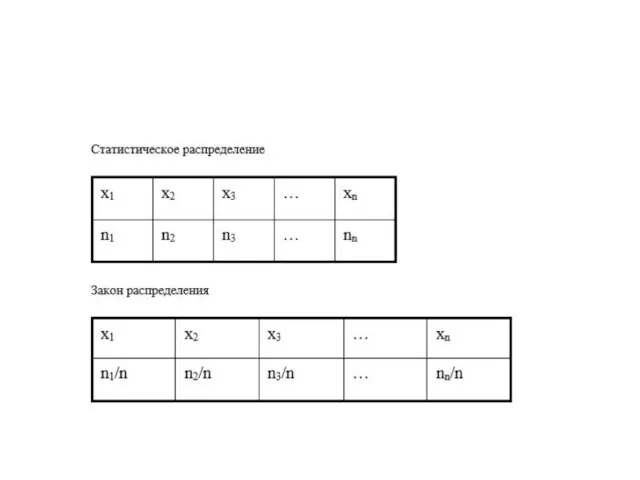
- 15. Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение удобно
- 17. Пример1. Для выборки определить объем, размах, найти статистический ряд и выборочное распределение: 3, 8, -1, 3,
- 18. Пример 2. В результате 10 опытов получена выборка 2,2,2,3,4,4,6,6,6,6, тогда для нее закон распределения будет?
- 20. Скачать презентацию













 Наибольшие и найменьшее значение функции
Наибольшие и найменьшее значение функции Кубический корень
Кубический корень Основные характеристики средств измерений. Лекция 4
Основные характеристики средств измерений. Лекция 4 Логарифмическая функция. Тест
Логарифмическая функция. Тест Уравнение плоскости
Уравнение плоскости Цели урока:
Цели урока: Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление
Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление Простейшие уравнения
Простейшие уравнения Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Геологические приложения одномерной статистической модели
Геологические приложения одномерной статистической модели Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся
Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся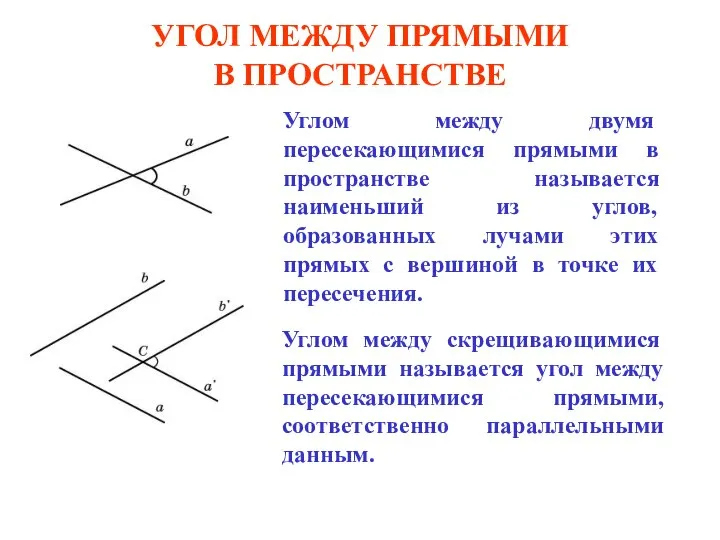 Угол между двумя прямыми в пространстве Вариант 2.ppt
Угол между двумя прямыми в пространстве Вариант 2.ppt Геометрические тела. Обьём прямоугольного параллелепипеда. 5 класс
Геометрические тела. Обьём прямоугольного параллелепипеда. 5 класс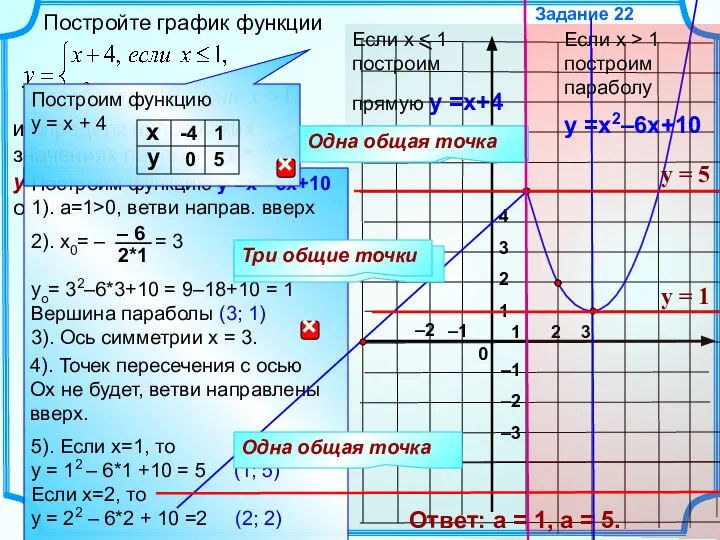 Парабола прямая. Часть II
Парабола прямая. Часть II Второй признак подобия треугольников
Второй признак подобия треугольников Степень с натуральным показателем. Обобщающий урок в 7 классе
Степень с натуральным показателем. Обобщающий урок в 7 классе Решение задач
Решение задач Пирамида
Пирамида Презентация на тему Решение неравенств методом интервалов (9 класс)
Презентация на тему Решение неравенств методом интервалов (9 класс)  Упрощение выражений. Тест
Упрощение выражений. Тест Сумма углов треугольника
Сумма углов треугольника Вычисление производной и правила дифференцирования
Вычисление производной и правила дифференцирования Умножение и деление смешанных дробей
Умножение и деление смешанных дробей Математическая тревожность
Математическая тревожность Решение логарифмических уравнений
Решение логарифмических уравнений Решение систем неравенств
Решение систем неравенств Семь чудес Кузбасса 5 класс
Семь чудес Кузбасса 5 класс Признаки равенства треугольников
Признаки равенства треугольников