Содержание
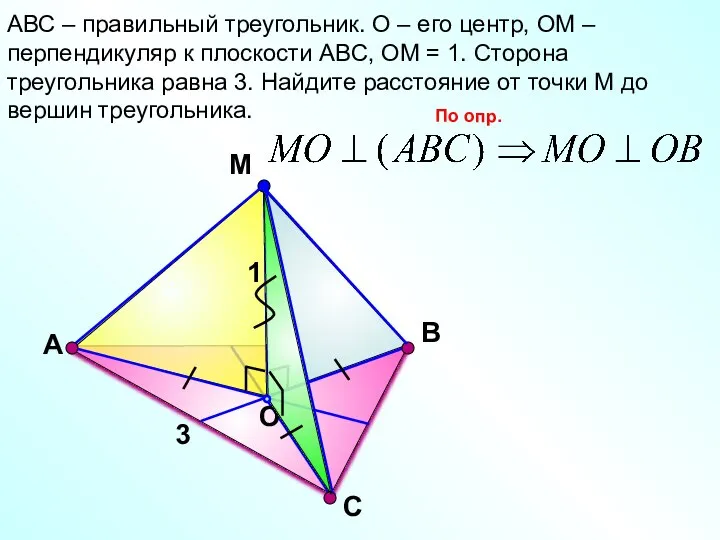
- 2. С М O В АВС – правильный треугольник. О – его центр, ОМ – перпендикуляр к
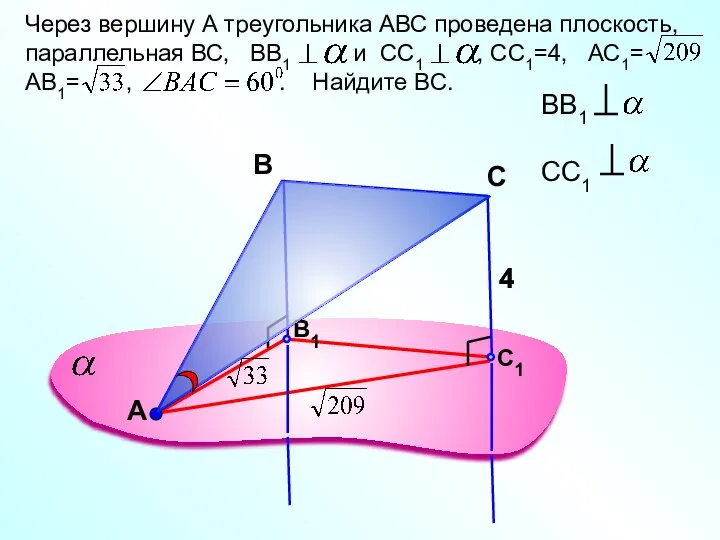
- 3. А Через вершину А треугольника АВС проведена плоскость, параллельная ВС, ВВ1 и СС1 , СС1=4, АС1=
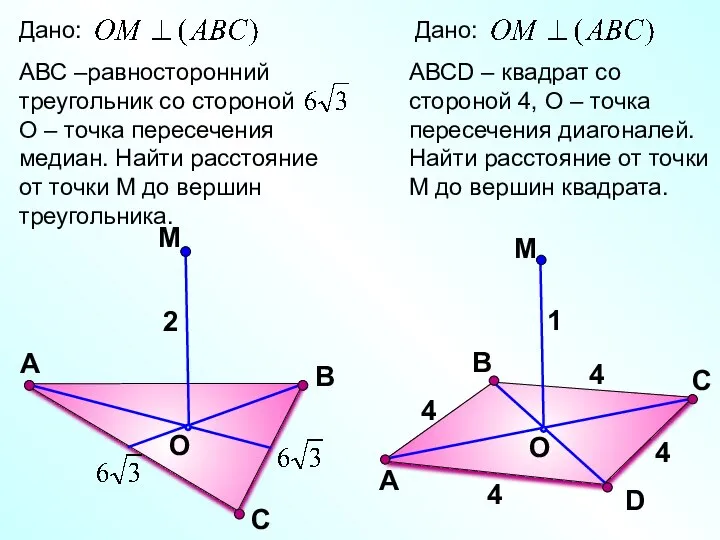
- 4. С М O В А 2 D В М O С А АВСD – квадрат со
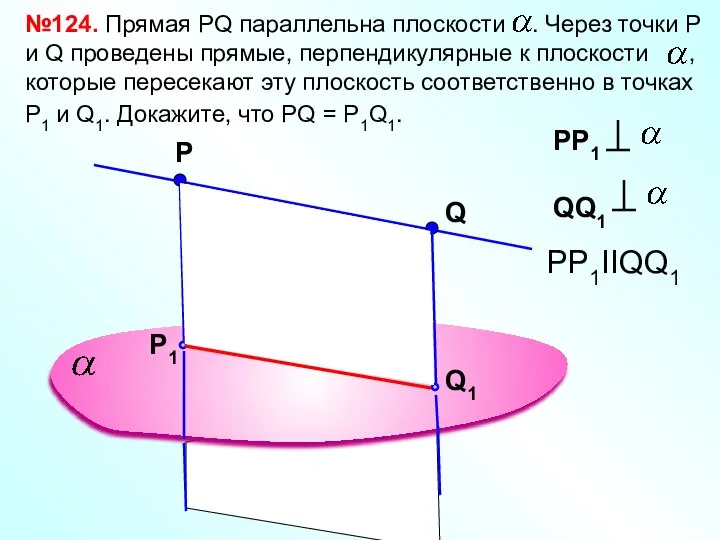
- 5. Р №124. Прямая РQ параллельна плоскости . Через точки Р и Q проведены прямые, перпендикулярные к
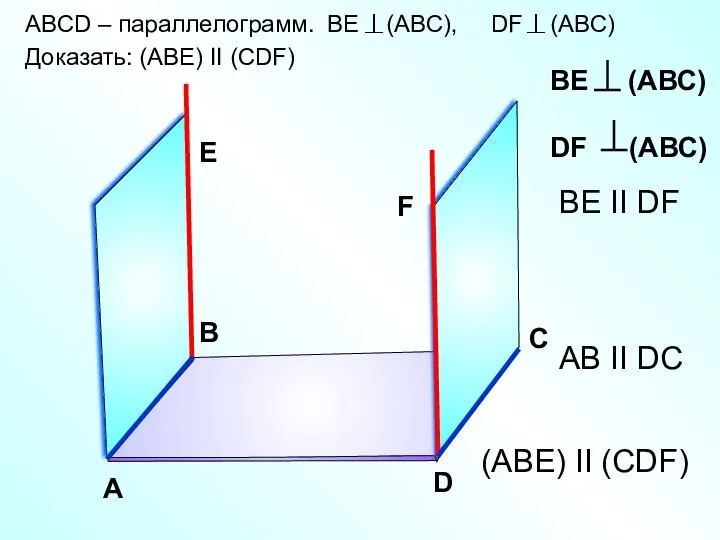
- 6. ABCD – параллелограмм. BE (ABC), DF (ABC) Доказать: (АВЕ) II (СDF) А В С D ВЕ
- 8. Скачать презентацию
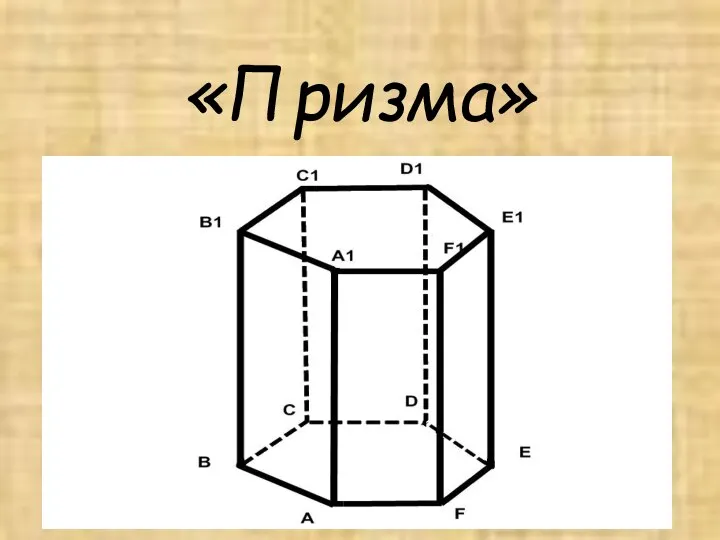 Призма. Определение призмы
Призма. Определение призмы Аналитическая геометрия на плоскости (лекция 1-2)
Аналитическая геометрия на плоскости (лекция 1-2) Презентация на тему СРАВНЕНИЕ ОТРЕЗКОВ И УГЛОВ
Презентация на тему СРАВНЕНИЕ ОТРЕЗКОВ И УГЛОВ  Презентация на тему Решение неравенств с одной переменной (11 класс)
Презентация на тему Решение неравенств с одной переменной (11 класс) 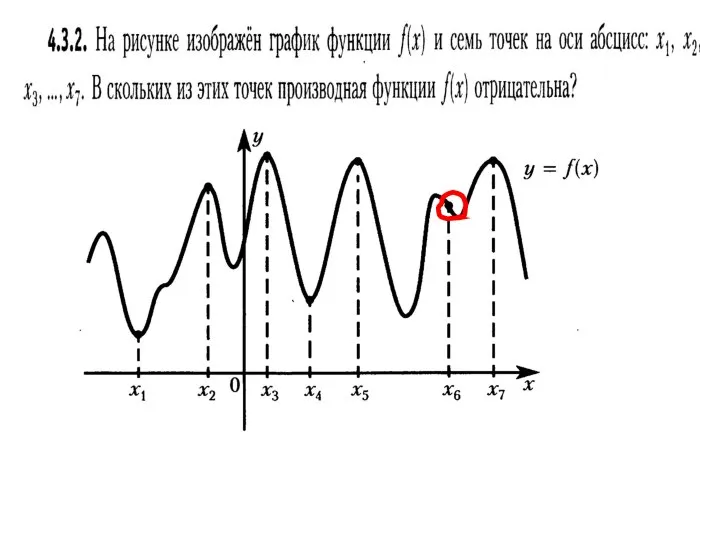 Графики функций
Графики функций Треугольник
Треугольник Тела вращения
Тела вращения Периметр и площадь прямоугольника
Периметр и площадь прямоугольника Повторение.Геометрия(ЕМН) 10 класс
Повторение.Геометрия(ЕМН) 10 класс Графики функций
Графики функций Преобразование чисел, полученных при измерении мерами стоимости, длины, массы
Преобразование чисел, полученных при измерении мерами стоимости, длины, массы Проекция группы геометрических тел
Проекция группы геометрических тел Предел функции
Предел функции Подготовка к ЕГЭ (профильный уровень). Теория вероятности
Подготовка к ЕГЭ (профильный уровень). Теория вероятности Оптимизация функций одной переменной
Оптимизация функций одной переменной Основы анализа данных. Регрессионный анализ. (Лекция 6)
Основы анализа данных. Регрессионный анализ. (Лекция 6) В стране математики
В стране математики Сложение вида +7
Сложение вида +7 Решение задач на части
Решение задач на части Моделирование. Объекты и их модели. (Тема 10)
Моделирование. Объекты и их модели. (Тема 10) Линейная алгебра. Лекция №2. Часть 2
Линейная алгебра. Лекция №2. Часть 2 Геометрические фигуры
Геометрические фигуры Считаем в уме легко! Умножение на 11
Считаем в уме легко! Умножение на 11 Симметрия и асимметрия
Симметрия и асимметрия Решение тригонометрических уравнений, приводимых калгебраическим
Решение тригонометрических уравнений, приводимых калгебраическим Числовая последовательность
Числовая последовательность Окружность. Повторение
Окружность. Повторение Литература
Литература