Слайд 4Термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование

функции на возрастание или убывание называют исследованием функции на монотонность.
Если функция возрастает (или убывает) на своей области определения, то говорят, что функция возрастающая (убывающая).
Слайд 5Пример
Исследовать на монотонность функцию y=5-2x
Решение:
f(x)=5-2x
x1 -2x1>-2x2
5-2x1>5-2x2
То есть f(x1)>f(x2).
Из неравенства

x1
f(x2), а это означает, что заданная функция убывает на всей числовой прямой.
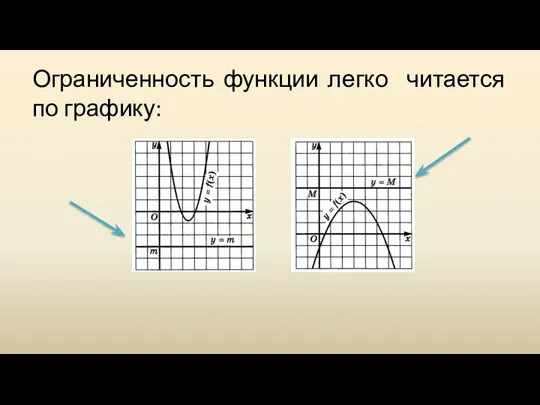
Слайд 9Если множество Х не указано, то подра-зумевается, что речь идет об ограниченности

функции сверху или снизу на всей области ее определения.
Если функция ограничена и сверху и снизу на всей области определения, то ее называют ограниченной.
Слайд 10Ограниченность функции легко читается по графику:
Слайд 15Если множество Х не указано, то подразумевается, что речь идет об поиске

наименьшего или наибольшего значения функции на всей области ее определения.
Слайд 16Утверждения:
1) Если у функции существует yнаим, то она ограничена снизу.
2) Если у

функции существует yнаиб, то она ограничена сверху.
3) Если функция не ограничена снизу, то у нее не существует унаим .
4) Если функция не ограничена сверху, то у нее не существует унаиб .
Слайд 19Если график функции f(x) на промежутке Х не имеет точек разрыва (то

есть представляет собой сплошную линию), то это значит, что функция f(x) непрерывна на промежутке Х.
Замечание: Обсуждая последние два свойст-ва, мы будем пока по-прежнему опираться на наглядно-интуитивные представления. До-казательство этих свойств будет рассмотрено нами позже.
Слайд 20Функцию f(x), xϵX называют четной, если для любого значения х из множества

Х выполняется равенство:
f(-x)=f(x)
Функцию f(x), xϵX называют нечетной, если для любого значения х из множества Х выполняется равенство:
f(-x)=-f(x)
Слайд 21В определениях идет речь о значениях функции в точках -х и х.

Тем самым предполагается, что функция определена и в точке х и в точке -х. Это значит, что точки х и -х одновременно принадлежат области определения функции. Если числовое множество Х вместе с каждым своим элементом х содержит и противоположный элемент -х, то такое множество называют симметричным множеством.
Например: отрезок [-5, 5] ̶ симметричное множество, а отрезок [-4, 5] ̶ не симметричное множество (в него входит число 5, но не входит противоположное ему -5)
Слайд 22Если функция у=f(x), хϵХ четная или нечетная, то ее область определения Х

– симметричное множество.
Если же Х – несимметричное множество, то функция у=f(x), хϵХ не может быть ни четной ни нечетной.
Слайд 23Алгоритм исследования функции y=f(x), хϵХ на четность.
Установить, симметрична ли область определения

функции. Если нет, то объявить, что функция не является ни четной, ни нечетной. Если да, то перейти ко второму шагу алгоритма.
Составить выражение f(-x).
Сравнить f(-x) и f(x):
а) если f(-x)=f(x), то функция четная;
б) если f(-x)=-f(x), то функция нечетная;
в) если хотя бы в одной точке хϵХ выполняется соотношение f(-x)≠f(x) и хотя бы в одной точке хϵХ выполняется соотношениеf(-x)≠-f(x), то функция не является ни четной, ни нечетной.
Слайд 27График четной функции симметричен относительно оси у.
Если график функции y=f(x), хϵХ симметричен
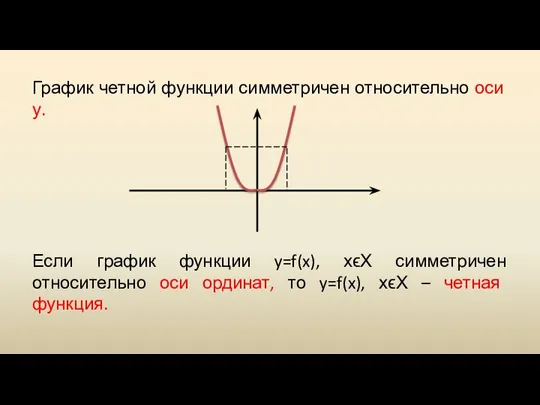
относительно оси ординат, то y=f(x), хϵХ – четная функция.
Слайд 28График нечетной функции симметричен относительно начала координат.
Если график функции y=f(x), хϵХ симметричен
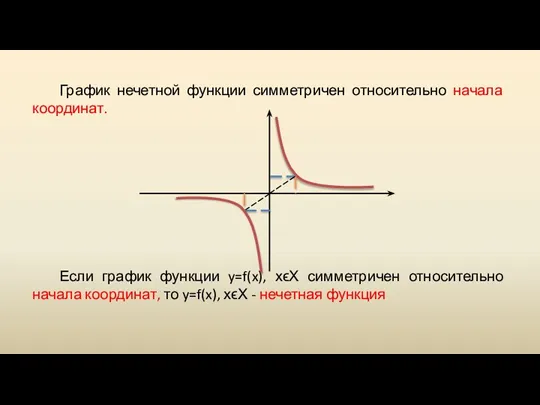
относительно начала координат, то y=f(x), хϵХ - нечетная функция


























 Повторение изученного материала. 1 класс
Повторение изученного материала. 1 класс Приближенные вычисления
Приближенные вычисления Иррациональные уравнения
Иррациональные уравнения Презентация на тему Первообразная и неопределенный интеграл
Презентация на тему Первообразная и неопределенный интеграл  Презентация на тему Приближённые вычисления
Презентация на тему Приближённые вычисления  Зимующие птицы. Дети 5 лет
Зимующие птицы. Дети 5 лет Решите уравнение (вариант 26 )
Решите уравнение (вариант 26 ) Перпендикулярные прямые в пространстве
Перпендикулярные прямые в пространстве Теория вероятности. События и испытания
Теория вероятности. События и испытания Тригонометрические функции
Тригонометрические функции Экстремумы функции
Экстремумы функции Корреляции и корреляционные уравнения
Корреляции и корреляционные уравнения Математический расчет или интуиция, что надежней?
Математический расчет или интуиция, что надежней? Способы решения уравнений с модулями
Способы решения уравнений с модулями Объем шара и площадь сферы
Объем шара и площадь сферы Письмово в робочий зошит
Письмово в робочий зошит Цилиндр и конус. (Часть 2)
Цилиндр и конус. (Часть 2) Содержание кривых участков пути. Переходные кривые
Содержание кривых участков пути. Переходные кривые Построение треугольника по трем элементам
Построение треугольника по трем элементам Порядок выполнения действий в выражениях
Порядок выполнения действий в выражениях TOChEChNAYa_I_INTERVAL_NAYa_OTsENKA_SLUChAJNOJ_VELIChINY (1)
TOChEChNAYa_I_INTERVAL_NAYa_OTsENKA_SLUChAJNOJ_VELIChINY (1) parallelogramm._svoystva_parallelogramma
parallelogramm._svoystva_parallelogramma Математическая игра-раскраска Обезьянка
Математическая игра-раскраска Обезьянка Лето в цифрах. Маршрут поездки
Лето в цифрах. Маршрут поездки Линейная функция
Линейная функция Уравнение сферы
Уравнение сферы Занимательные задачи (4 класс)
Занимательные задачи (4 класс) Использование кватернионов в решении задачи навигации в трехмерном пространстве при помощи выделенных линейных объектов
Использование кватернионов в решении задачи навигации в трехмерном пространстве при помощи выделенных линейных объектов