Содержание
- 2. Цели урока: Ввести понятие параллелограмма и рассмотреть его свойства. Научить учащихся применять свойства параллелограмма при решении
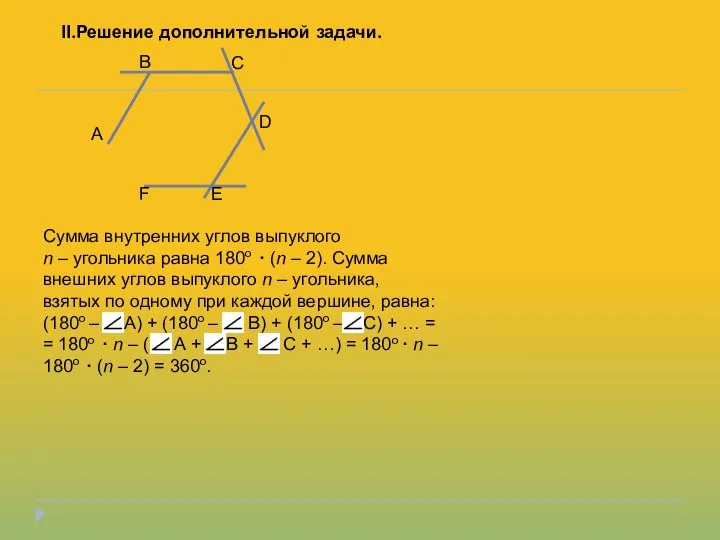
- 3. Сумма внутренних углов выпуклого n – угольника равна 180о · (n – 2). Сумма внешних углов
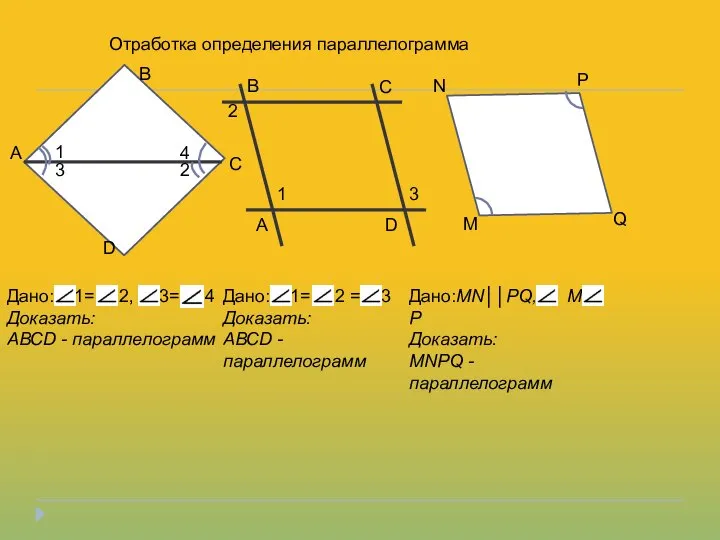
- 4. Отработка определения параллелограмма А В С D 1 2 3 4 B C D A 1
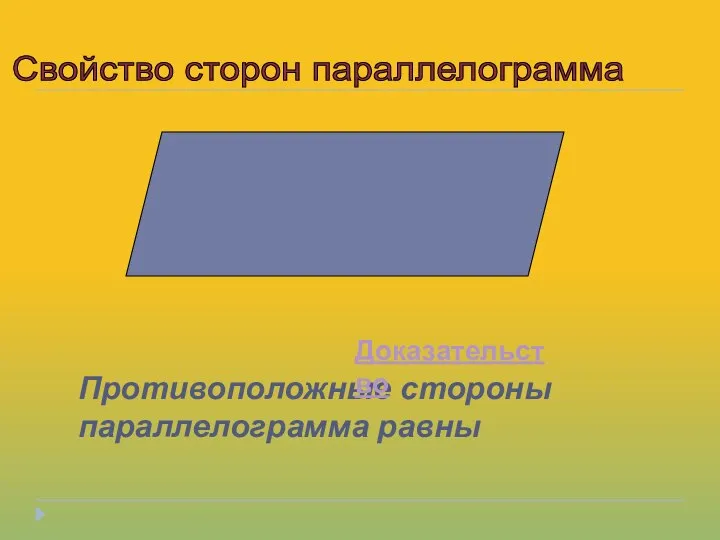
- 5. Противоположные стороны параллелограмма равны Свойство сторон параллелограмма Доказательство
- 6. Противоположные углы параллелограмма равны Свойство углов параллелограмма Доказательство:
- 7. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам Свойство диагоналей параллелограмма Доказательство:
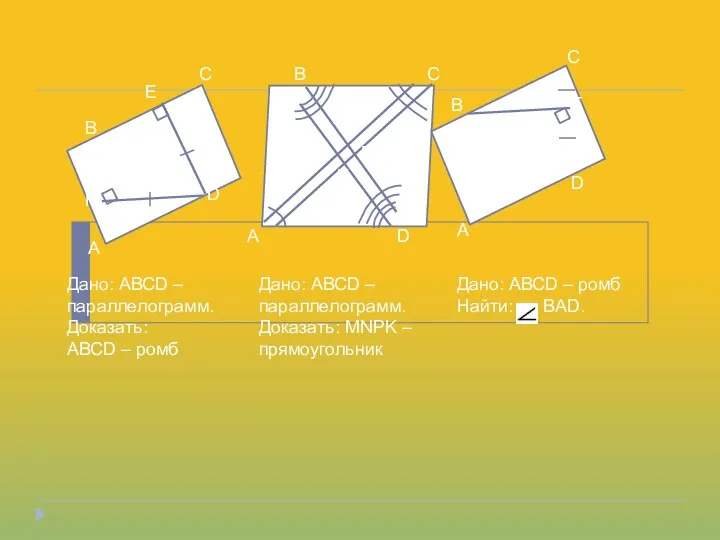
- 8. Решите задачи
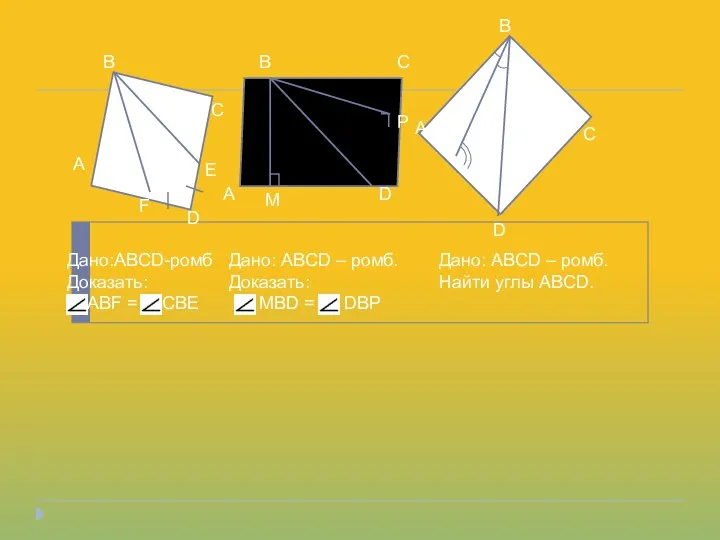
- 9. A B C E D F A B C D M P A B C D
- 10. В Е С А F D B C D A M N P K B C
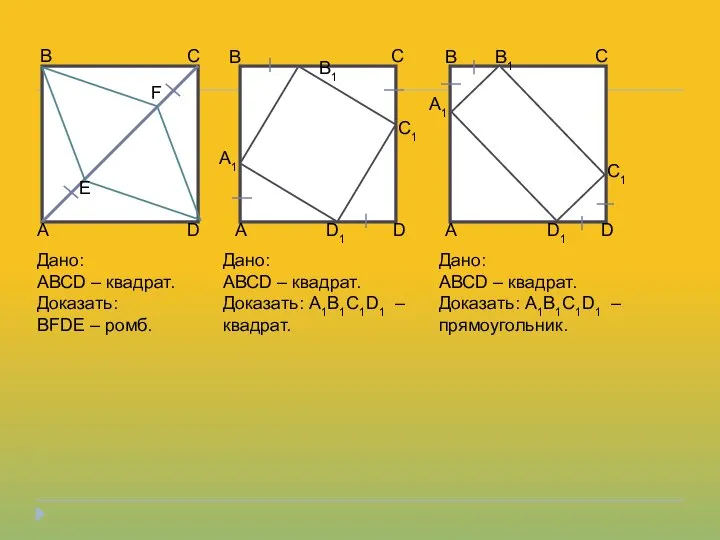
- 11. B C B B1 C C1 A D A E F A1 D D1 B B1
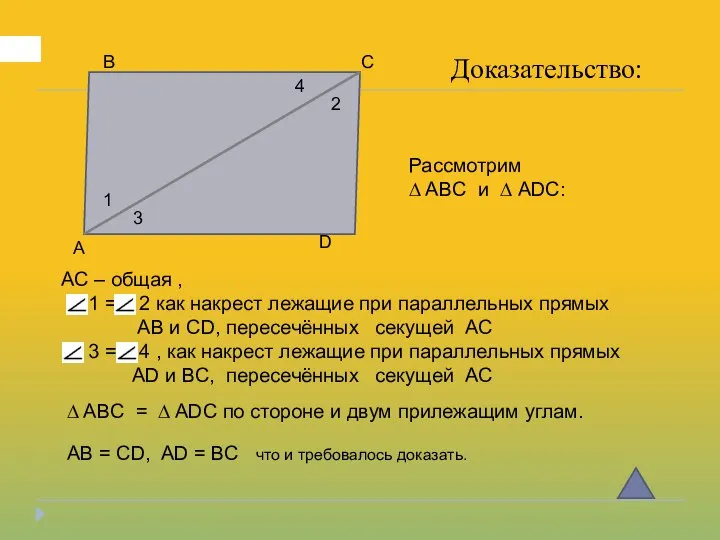
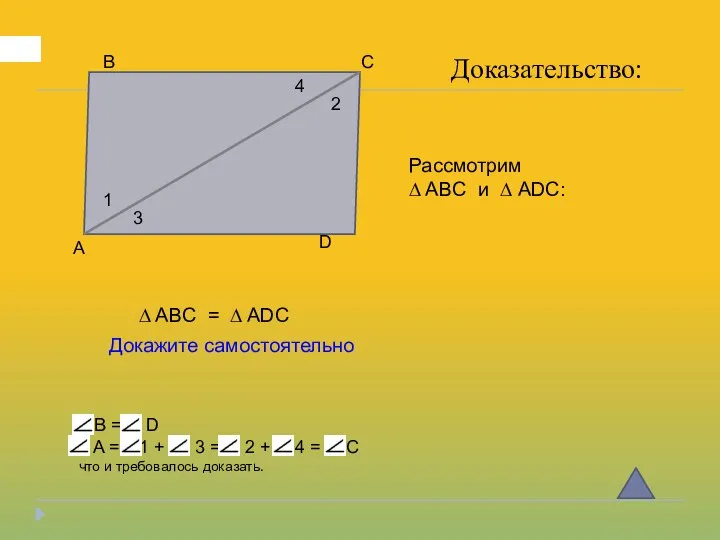
- 13. А В С D Доказательство: 1 2 3 4 AC – общая , 1 = 2
- 14. А В С D Доказательство: 1 2 3 4 ∆ ABC = ∆ ADC Рассмотрим ∆
- 16. Скачать презентацию




 Линейные операции над векторами
Линейные операции над векторами Решение задачи с использованием циклов
Решение задачи с использованием циклов Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Переместительное свойство умножения
Переместительное свойство умножения Математический тренажёр Бабушкины примеры
Математический тренажёр Бабушкины примеры Модуль комплексного числа
Модуль комплексного числа Учебный проект по алгебре Наш класс оценивает статистика
Учебный проект по алгебре Наш класс оценивает статистика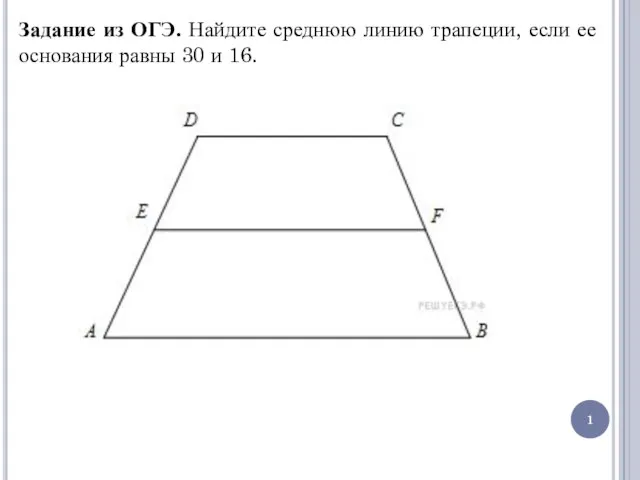 Прямоугольник. Ромб. Квадрат. Задание из ОГЭ
Прямоугольник. Ромб. Квадрат. Задание из ОГЭ Решение задач. Длина окружности. Площадь круга
Решение задач. Длина окружности. Площадь круга Заниматика. Миром управляют числа
Заниматика. Миром управляют числа СДНФ и СКНФ — два представления булевой функции
СДНФ и СКНФ — два представления булевой функции Экономические задачи
Экономические задачи Подобие треугольников и решение практических задач задач
Подобие треугольников и решение практических задач задач Презентация на тему Логарифмы с параметрами
Презентация на тему Логарифмы с параметрами  Задачи про виноград и изюм
Задачи про виноград и изюм Весёлая математика. Сколько в ширину? Сколько в высоту? Карточки для детей
Весёлая математика. Сколько в ширину? Сколько в высоту? Карточки для детей Изучение таблицы деления
Изучение таблицы деления Смешанные дроби. 5 клас
Смешанные дроби. 5 клас Действительный анализ. Глава 2. Измеримые множества
Действительный анализ. Глава 2. Измеримые множества Формула суммы п первых членов геометрической прогрессии
Формула суммы п первых членов геометрической прогрессии Иррациональные уравнения
Иррациональные уравнения Задачи на проценты
Задачи на проценты Решение примеров
Решение примеров Действительные числа. Практикум по математике. Занятие №1
Действительные числа. Практикум по математике. Занятие №1 Презентация на тему ГИА 2013. Модуль «Алгебра» №7
Презентация на тему ГИА 2013. Модуль «Алгебра» №7  Свойства арифметического корня
Свойства арифметического корня Скалярное произведение векторов. Задания
Скалярное произведение векторов. Задания Тренажер Состав числа
Тренажер Состав числа