Содержание
- 2. 17.08.2020
- 3. 17.08.2020 Основные сведения о матрицах Операции над матрицами Свойства алгебраических операций над матрицами План
- 4. Применение матричного исчисления Матричное исчисление положено в основу математического аппарата квантовой и статической механики, квантовой физики,
- 5. Матричное исчисление значительно упрощает описание электромагнитных процессов в цепях Матричное исчисление облегчает решение системы линейных уравнений
- 6. Матричное исчисление играет большую роль в решении ряда прикладных задач. На нем базируется теория колебаний в
- 7. К задачам линейной алгебры сводятся многочисленные алгоритмы обработки экспериментальных данных, минимизации линейных форм, различные задачи теории
- 8. 17.08.2020 1. Основные сведения о матрицах. Определение: Система действительных чисел (или элементов матрицы), расположенных в прямоугольную
- 9. 17.08.2020 Матрицу можно записывать коротко: в виде или в виде , где - элемент данной матрицы
- 10. 17.08.2020 Элементы матрицы образуют столбцы и строки. Первый индекс i указывает номер строки, а второй j
- 11. 17.08.2020 Например, элемент матрицы находится на пересечении второй строки и третьего столбца и равен Элемент
- 12. 17.08.2020 Набор называют строкой матрицы . Набор называют столбцом.
- 13. 17.08.2020 Если хотят указать размер матрицы, то пишут , это означает, что в матрице строк и
- 14. 17.08.2020 Например, матрица имеет порядок , т.е. . Элемент данной матрицы равен (?)
- 15. 17.08.2020 МОЛОДЦЫ! Верно,
- 16. 17.08.2020 Типы матриц 1. Если матрица содержит только одну строку – это вектор-строка (или строчная матрица).
- 17. 17.08.2020 3. Если , то матрица называется квадратной, а число – ее порядком. Элементы квадратной матрицы
- 18. 17.08.2020 4. Матрица, у которой все элементы, кроме диагональных, равны 0, называется диагональной и записывается в
- 19. 17.08.2020 5. Диагональная матрица вида называется единичной и обозначается или
- 20. 17.08.2020 6. Нулевая матрица (0) размера есть матрица этого размера, все элементы которой равны нулю: 7.
- 21. 17.08.2020 Определение. Две матрицы равны, если равны элементы, стоящие на одинаковых местах (при этом число строк
- 22. 17.08.2020 2. Операции над матрицами Операции над матрицами определяются с помощью операций над их элементами. Сложение
- 23. 17.08.2020 Например,
- 24. Замечание Строго говоря, операции вычитания матриц одного порядка А и В как таковой не существует. Разность
- 25. 17.08.2020 2. Произведением матрицы A на число λ называется матрица, у которой каждый элемент равен произведению
- 26. 17.08.2020 Например, если то
- 27. 17.08.2020 3. Произведением матрицы A, имеющей строк и столбцов, на матрицу , имеющую строк и столбцов,
- 28. 17.08.2020 ЗАМЕЧАНИЕ: если число столбцов первой матрицы и число строк второй матрицы не совпадают, то произведение
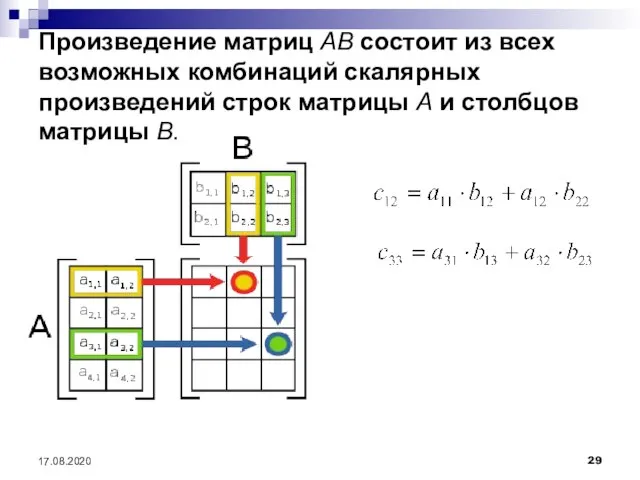
- 29. Произведение матриц AB состоит из всех возможных комбинаций скалярных произведений строк матрицы A и столбцов матрицы
- 30. 17.08.2020 В общем случае, произведение матриц не является коммутативной операцией. К примеру, элемент произведения матриц вычисляется
- 31. 17.08.2020 Например, Найти произведение 1) и 2) РЕШЕНИЕ 1)Укажем размеры заданных матриц: 2) Произведение матриц существует:
- 32. 3)Найдём элементы матрицы D: 17.08.2020
- 33. 4) Запишем матрицу D: 17.08.2020
- 34. 17.08.2020 5)
- 35. 17.08.2020 4. Умножение на единичную матрицу. Единичная матрица обладает замечательным свойством, а именно: умножение квадратной матрицы
- 36. 17.08.2020 Замечание: для произвольной матрицы и единичной матрицы переместительный закон умножения выполняется. Это свойство и объясняет
- 37. 17.08.2020 5. Транспонирование матриц Транспонированной к матрице называется матрица , в которой строки и столбцы поменялись
- 38. 17.08.2020 6. Возведение в степень Пусть – натуральное число. Для любой квадратной матрицы А степенью матрицы
- 39. 17.08.2020 3. Свойства алгебраических операций над матрицами 1. Свойства операций сложения 1. (ассоциативность сложения) 2. (коммутативность
- 40. 17.08.2020 Например, для матриц и
- 41. 17.08.2020 3. Дистрибутивность. Для любых матриц , у которых определены соответственно операции сложения и умножения, 4.
- 42. ? ЛИТЕРАТУРА Математики шутят 17.08.2020
- 44. Скачать презентацию








































 Произведение многочленов
Произведение многочленов Презентация на тему Небесная геометрия - снежинки
Презентация на тему Небесная геометрия - снежинки  Решение простейших тригонометрических неравенств
Решение простейших тригонометрических неравенств презентация к уроку по теме_ _Трапеция_ (8 класс, Атанасян)
презентация к уроку по теме_ _Трапеция_ (8 класс, Атанасян) Деление на натуральное число и деление на десятичную дробь
Деление на натуральное число и деление на десятичную дробь Деление десятичных дробей
Деление десятичных дробей Составление переводной работы по алгебре в формате ЕГЭ, 2017-2018 учебный год
Составление переводной работы по алгебре в формате ЕГЭ, 2017-2018 учебный год Комбинаторика. Курс лекций Дискретная математика
Комбинаторика. Курс лекций Дискретная математика Комбинаторика
Комбинаторика Карточки-задания по теме Конус. Содержат алгоритм решения
Карточки-задания по теме Конус. Содержат алгоритм решения Приближенные вычисления
Приближенные вычисления Касательная к окружности. Решение задач
Касательная к окружности. Решение задач Итоговый тест по алгебре для 7 класса
Итоговый тест по алгебре для 7 класса Презентация на тему Упрощение выражений (6 класс)
Презентация на тему Упрощение выражений (6 класс)  Уравнения, содержащие знак модуля
Уравнения, содержащие знак модуля Решение задания 12 ЕГЭ (профиль)
Решение задания 12 ЕГЭ (профиль) Семейство четырехугольников
Семейство четырехугольников ЛЕКЦИЯ_7
ЛЕКЦИЯ_7 Заниматика. Миром управляют числа
Заниматика. Миром управляют числа Деление дробей
Деление дробей Векторы в пространстве
Векторы в пространстве Умножение и деление десятичной дроби на 10, 100, 1000
Умножение и деление десятичной дроби на 10, 100, 1000 Подготовка к ВПР (8 класс)
Подготовка к ВПР (8 класс)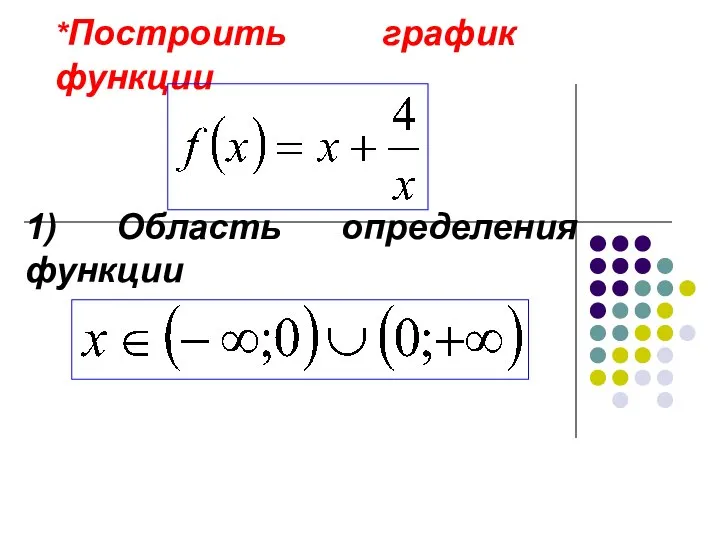 Построение графиков функций
Построение графиков функций Презентация на тему Деление десятичных дробей
Презентация на тему Деление десятичных дробей  Дидактический материал. Проверочные работы. Начальные понятия геометрии
Дидактический материал. Проверочные работы. Начальные понятия геометрии Призма. Площадь полной поверхности прямой призмы
Призма. Площадь полной поверхности прямой призмы Дифференциальные уравнения
Дифференциальные уравнения