Технология подготовки учащихся к овладению функционально-графическими методами решения задач с параметрами. (Занятие №3)
Содержание
- 2. Содержание курса 3
- 3. Содержание О функционально-графических методах решения задач с параметрами ЕГЭ 2014-2015 (что было и что предлагают в
- 4. О функционально-графическом методе решения задач с параметрами В задачах (уравнение, неравенство, система уравнений или неравенств) вида
- 5. О функционально-графических методах решения задач с параметрами Графический метод применительно к рассматриваемым задачам допускает несколько интерпретаций,
- 6. Плюсы и минусы графических методов в сравнении с аналитическими методами Применение графических методов оправдано в случаях,
- 7. Аналитический аппарат
- 8. Суть метода сечений для решения уравнений В случаях исследования уравнения на наличие корней или их количество
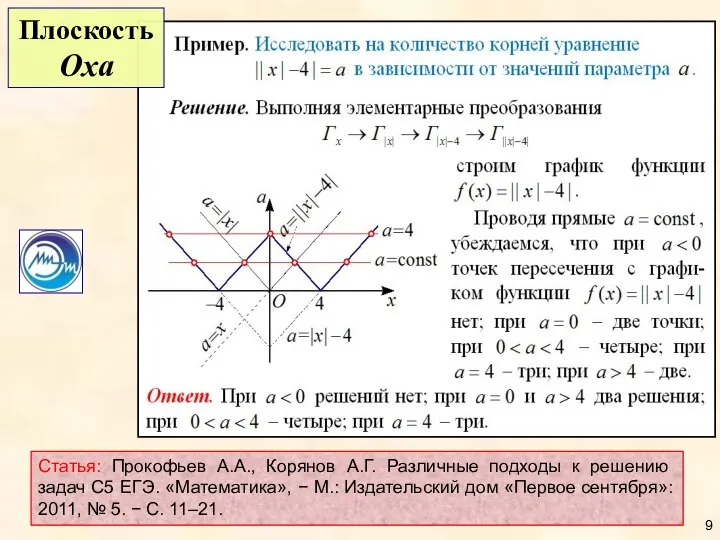
- 9. Статья: Прокофьев А.А., Корянов А.Г. Различные подходы к решению задач С5 ЕГЭ. «Математика», − М.: Издательский
- 10. Плоскость Oxy
- 11. ГИА 2010/14 (функционально-графический метод) Учащиеся 9 класса должны демонстрировать владение этими методами!
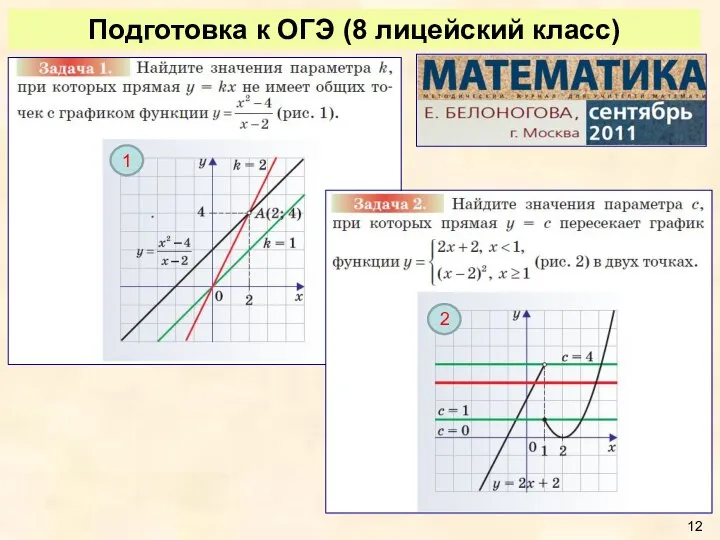
- 12. Подготовка к ОГЭ (8 лицейский класс) 1 2
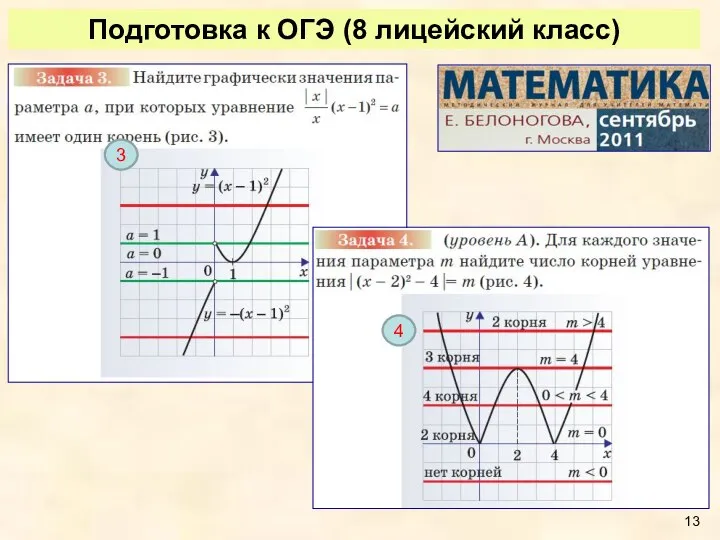
- 13. Подготовка к ОГЭ (8 лицейский класс) 3 4
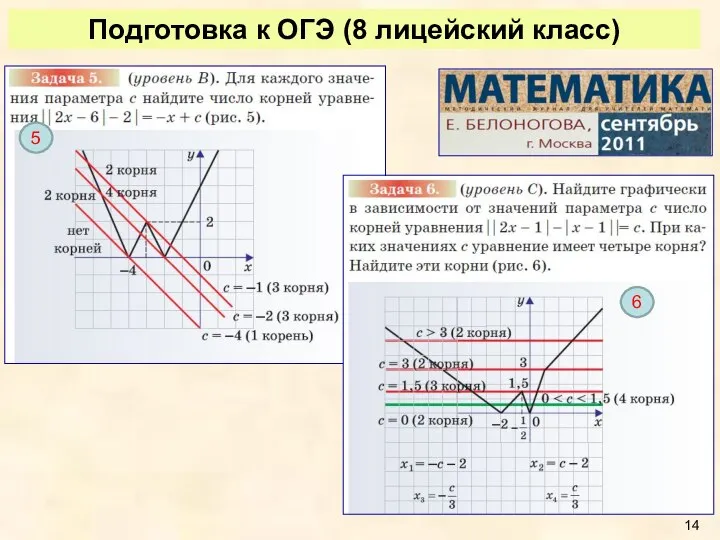
- 14. Подготовка к ОГЭ (8 лицейский класс) 5 6
- 15. Подготовка к ОГЭ (8 лицейский класс) 7 При разработке курса автором ставились следующие цели: развитие логического
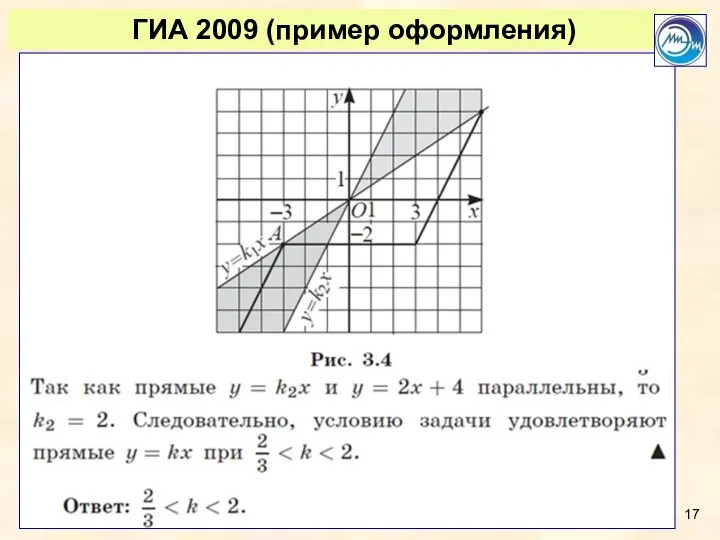
- 16. ГИА 2009 (пример оформления)
- 17. ГИА 2009 (пример оформления)
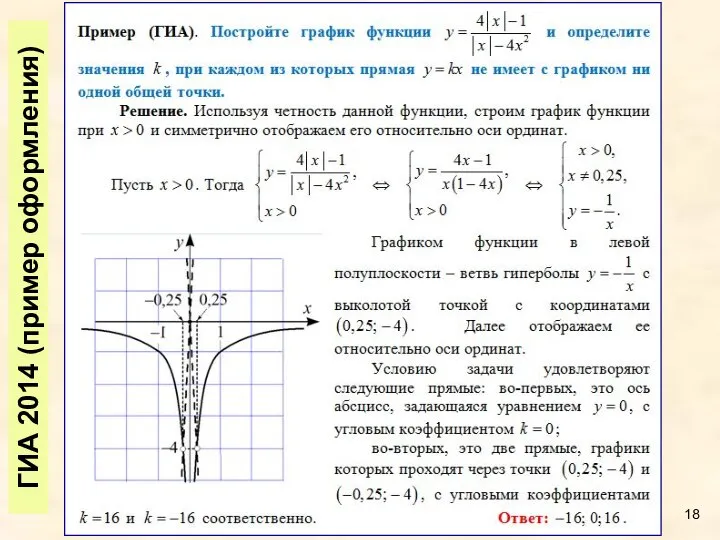
- 18. ГИА 2014 (пример оформления)
- 19. ЕГЭ 2010/14 (функционально-графический метод)
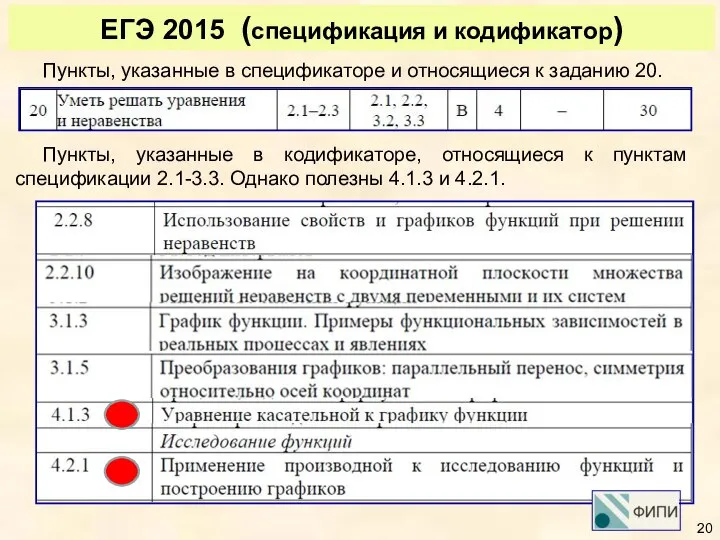
- 20. ЕГЭ 2015 (спецификация и кодификатор) Пункты, указанные в спецификаторе и относящиеся к заданию 20. Пункты, указанные
- 21. Литература для подготовки по заданию 20 ЕГЭ 2015 профильного уровней
- 22. Литература для подготовки по заданию 20 ЕГЭ 2015 профильного уровней
- 23. Классификация задач, решаемых функционально-графическими методами
- 24. Функционально-графические методы в электронных пособиях Прокофьева А.А. и Корянова А.Г. Адреса: http://alexlarin.net/ege/2012/C5-2012.http://alexlarin.net/ege/2012/C5-2012. html и http://www.alexlarin.net/ege/2011/c52011.html и
- 25. С чего следует начать? Для овладения графическими методами решения задач с параметрами необходимо повторить основные способы
- 26. Таблица элементарных преобразований графика функции
- 27. Последовательность действий при построении из графика функции графика функции
- 28. Задачи для самостоятельного решения функционально-графическим методом
- 29. Ответы к задачам для самостоятельного решения
- 30. Суть метода сечений для решения неравенств При решении или исследовании на наличие решений неравенства (или решений,
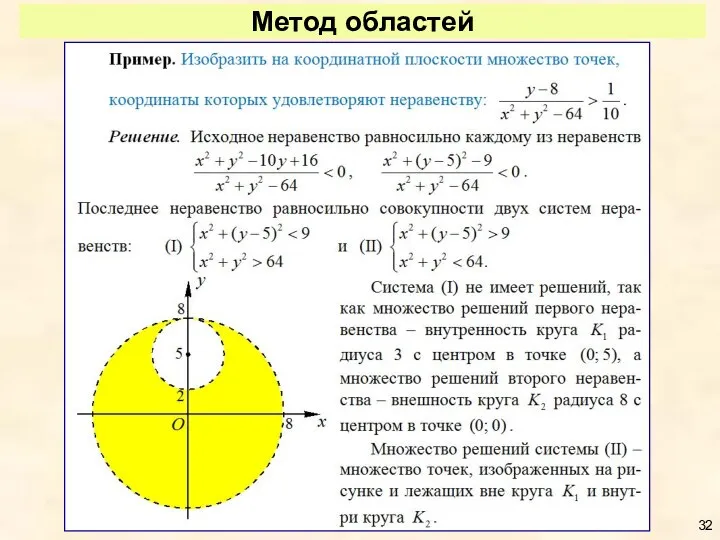
- 31. Метод областей Для изображения на координатной плоскости Oxy множества решений уравнений и неравенств с двумя переменными
- 32. Метод областей
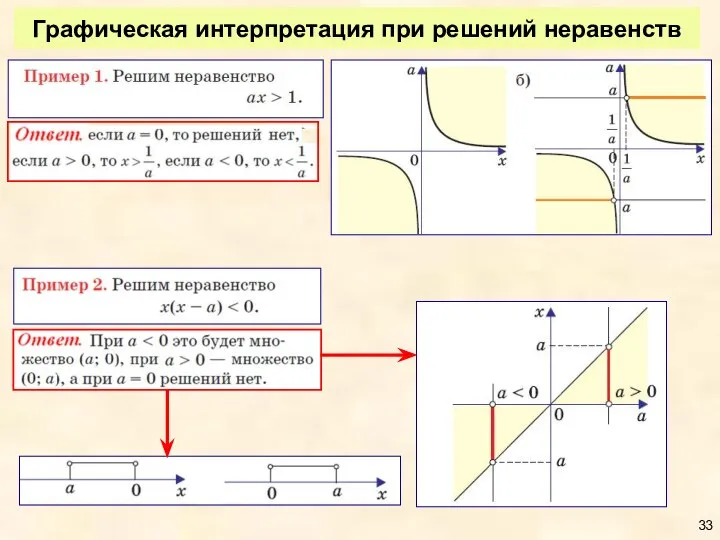
- 33. Графическая интерпретация при решений неравенств
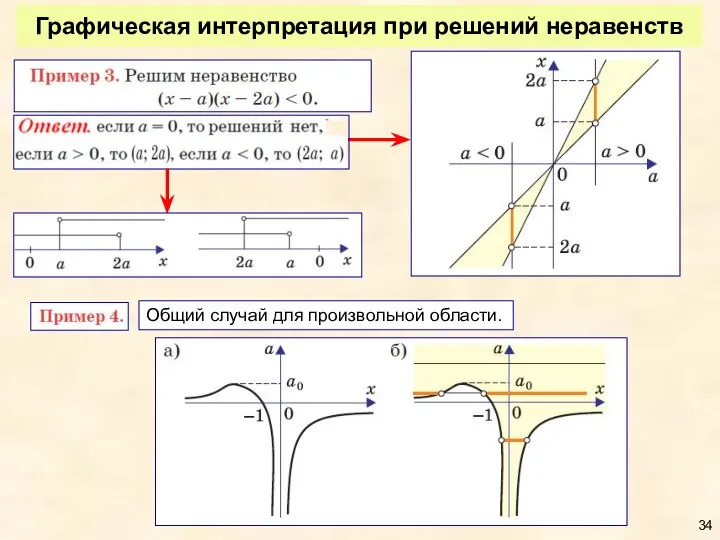
- 34. Графическая интерпретация при решений неравенств Общий случай для произвольной области.
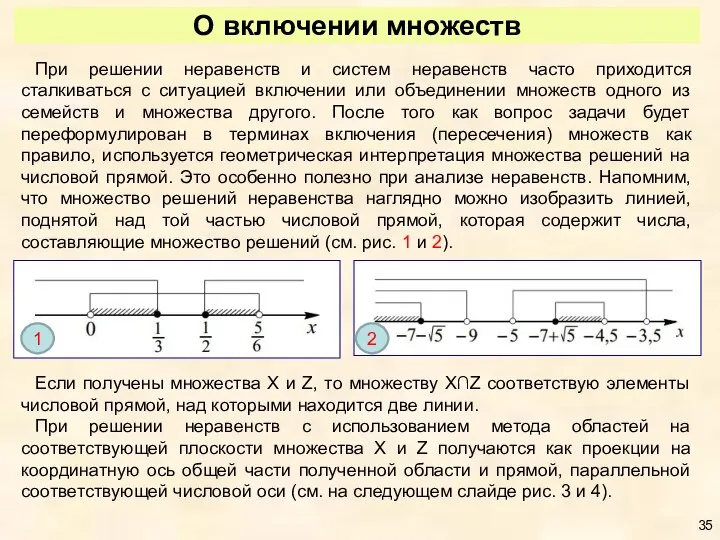
- 35. О включении множеств При решении неравенств и систем неравенств часто приходится сталкиваться с ситуацией включении или
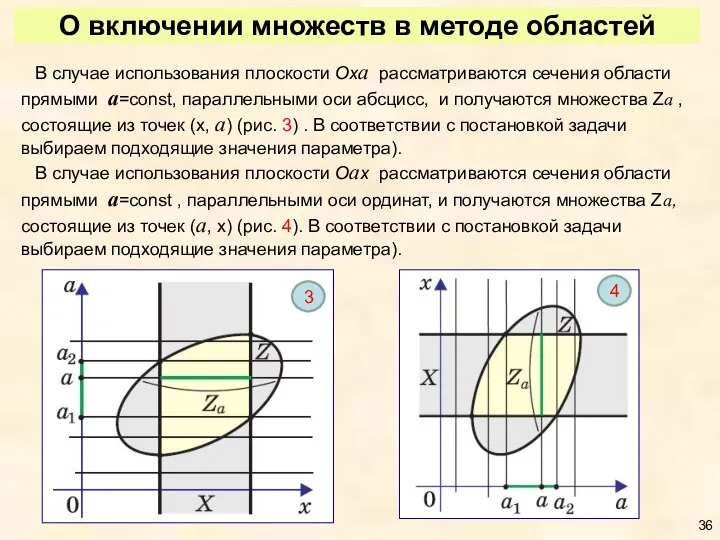
- 36. О включении множеств в методе областей В случае использования плоскости Oxa рассматриваются сечения области прямыми a=const,
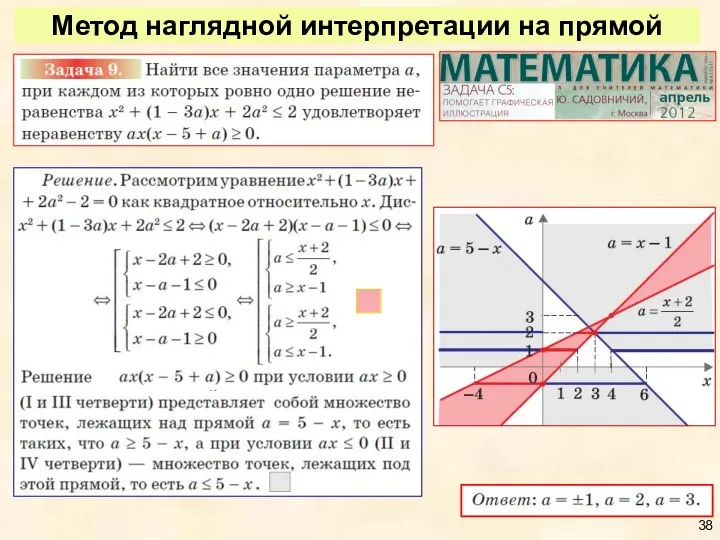
- 37. Метод наглядной интерпретации на прямой
- 38. Метод наглядной интерпретации на прямой
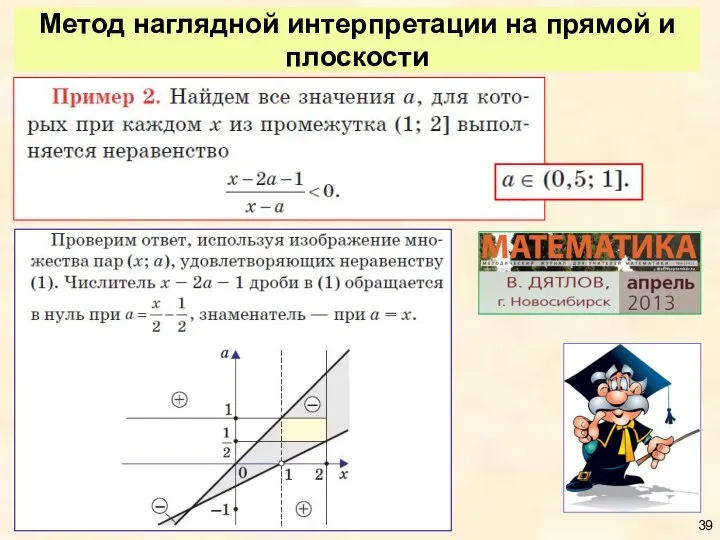
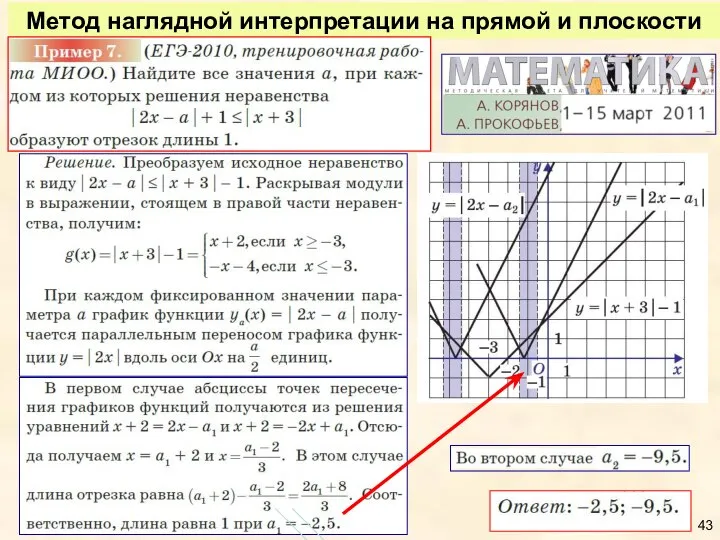
- 39. Метод наглядной интерпретации на прямой и плоскости
- 40. Метод наглядной интерпретации на прямой и плоскости
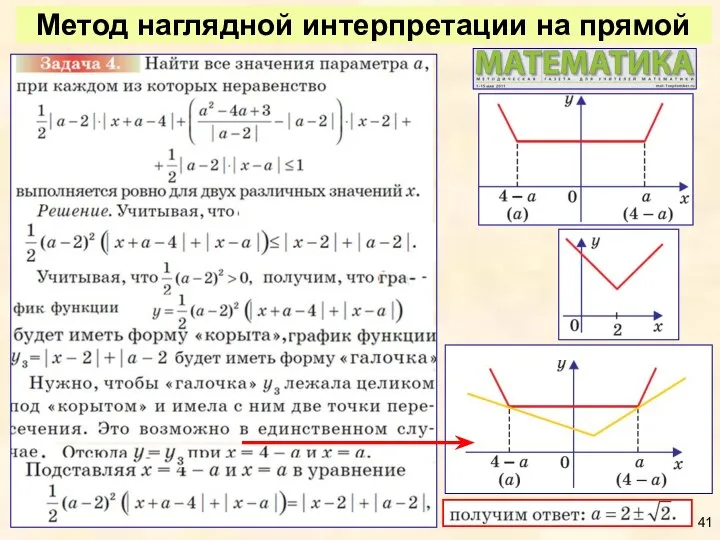
- 41. Метод наглядной интерпретации на прямой
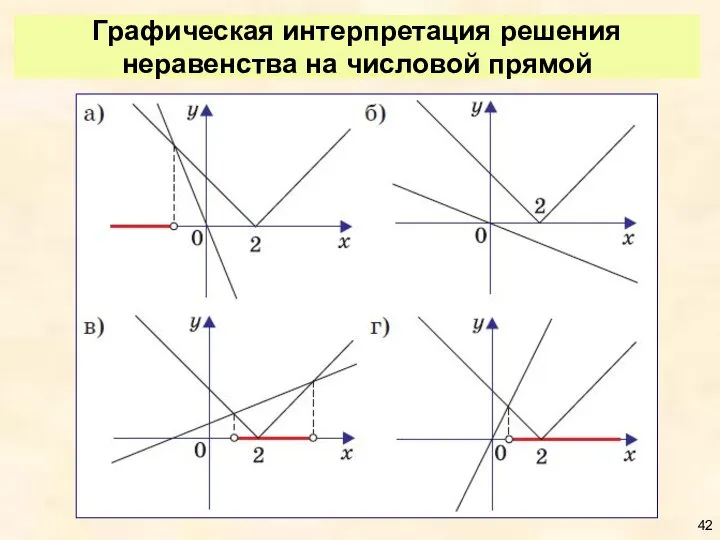
- 42. Графическая интерпретация решения неравенства на числовой прямой
- 43. Метод наглядной интерпретации на прямой и плоскости
- 44. Метод наглядной интерпретации на прямой и плоскости
- 45. Для самостоятельной работы
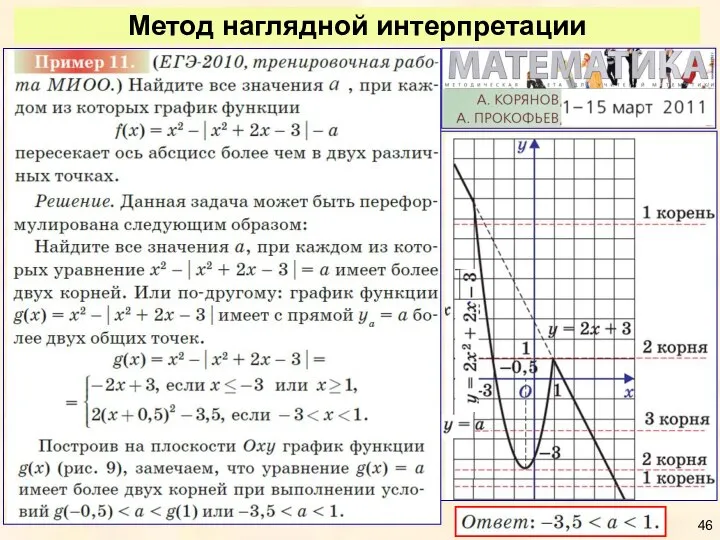
- 46. Метод наглядной интерпретации
- 47. Часто используемые семейства функций Рассмотрим часто встречающиеся в подобных задачах семейства функций или уравнения и их
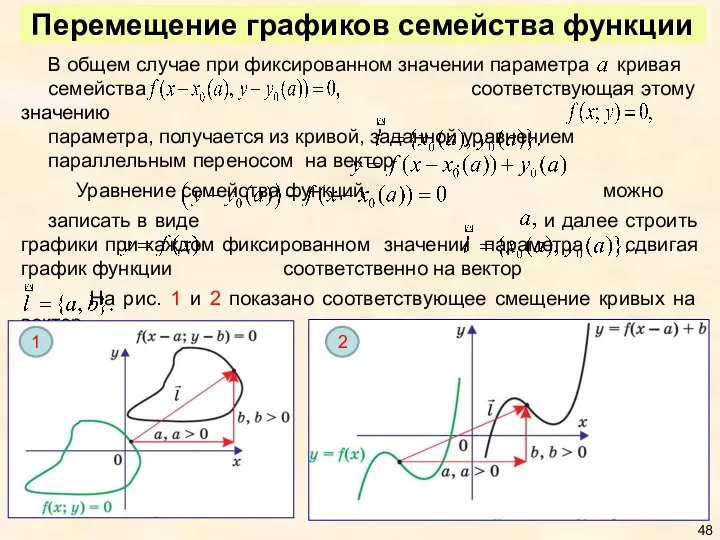
- 48. Перемещение графиков семейства функции В общем случае при фиксированном значении параметра кривая семейства соответствующая этому значению
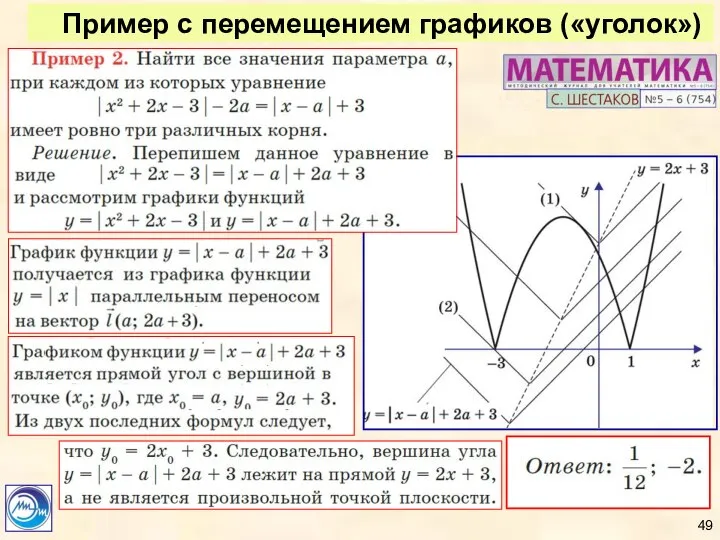
- 49. Пример с перемещением графиков («уголок»)
- 50. Пример с «пучком прямых» (ЕГЭ 2013)
- 51. Пример с «пучком прямых» (ЕГЭ 2013)
- 52. Окружность с изменяющимся радиусом
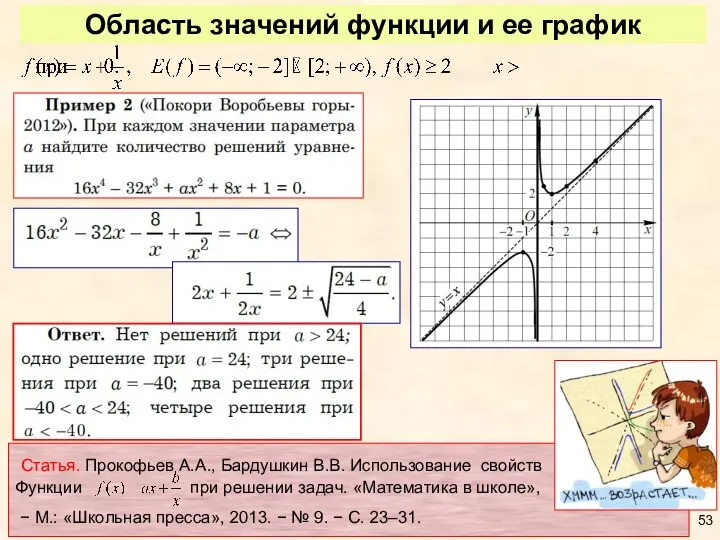
- 53. Область значений функции и ее график Статья. Прокофьев А.А., Бардушкин В.В. Использование свойств Функции при решении
- 54. Обучение графическим методам решения задач с параметром с использованием специализированных программ
- 58. Системы уравнений. С чего начать?
- 59. Система неравенств. Метод областей
- 60. Для самостоятельной работы. Метод областей
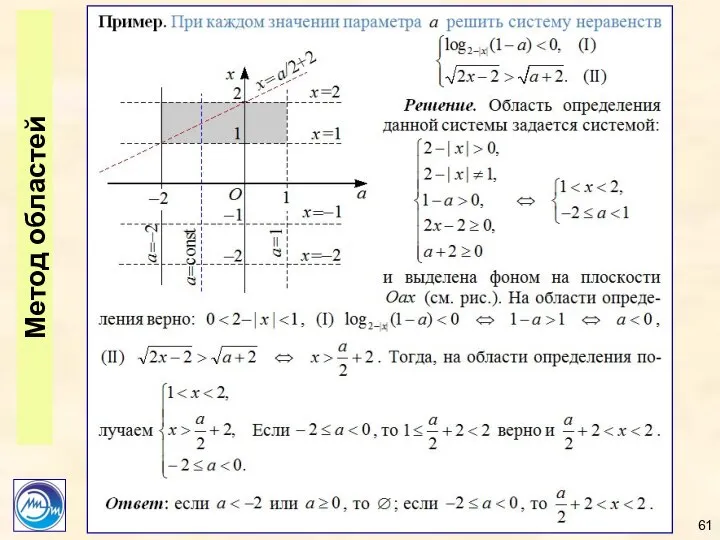
- 61. Метод областей
- 62. Системы уравнений и неравенств
- 63. Системы уравнений и неравенств Статья. Прокофьев А.А., Шабунин М.И. Системы уравнений и неравенств с двумя переменными.
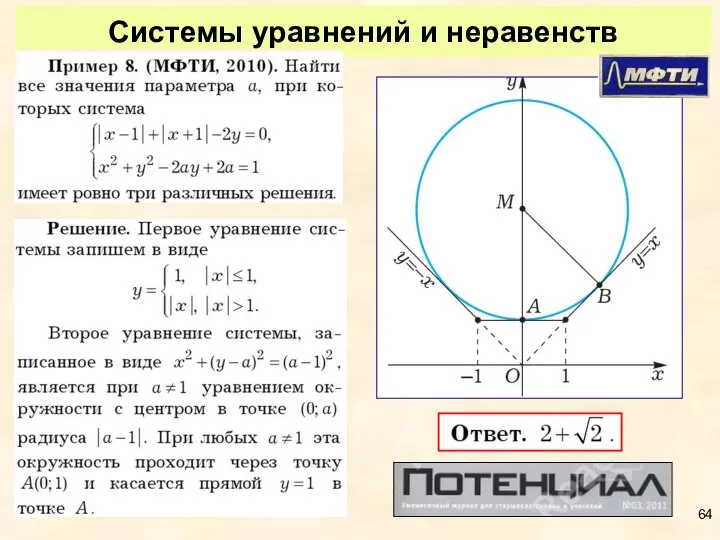
- 64. Системы уравнений и неравенств
- 65. Метод наглядной интерпретации на прямой и плоскости
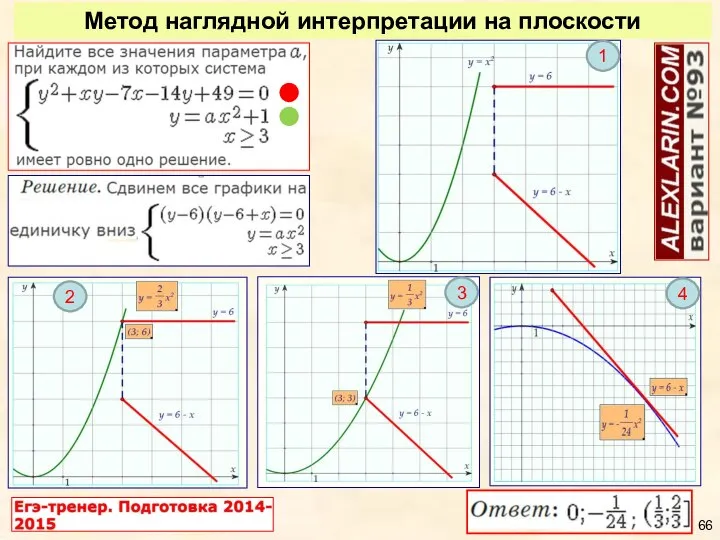
- 66. Метод наглядной интерпретации на плоскости 2 3 4 1
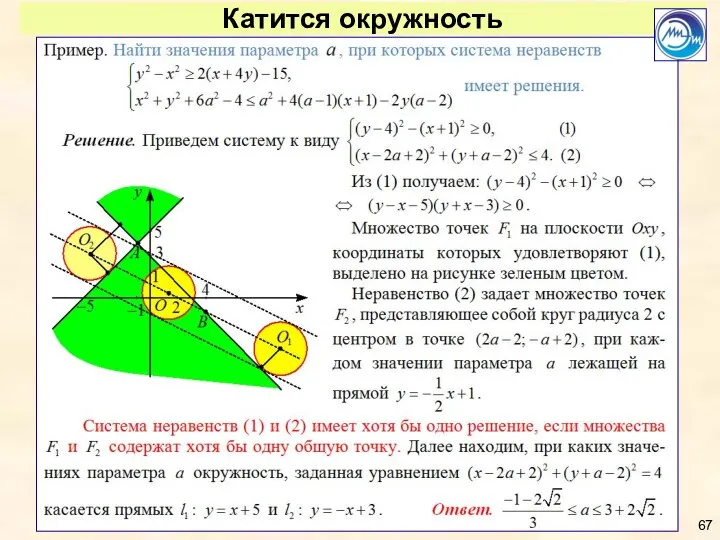
- 67. Катится окружность
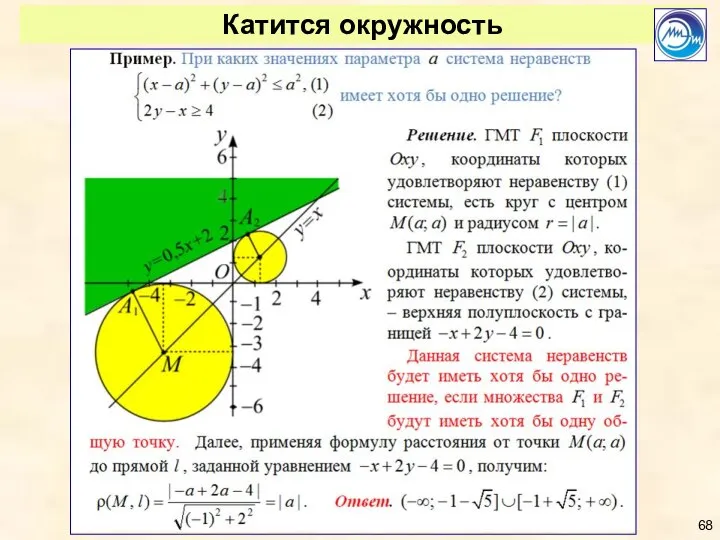
- 68. Катится окружность
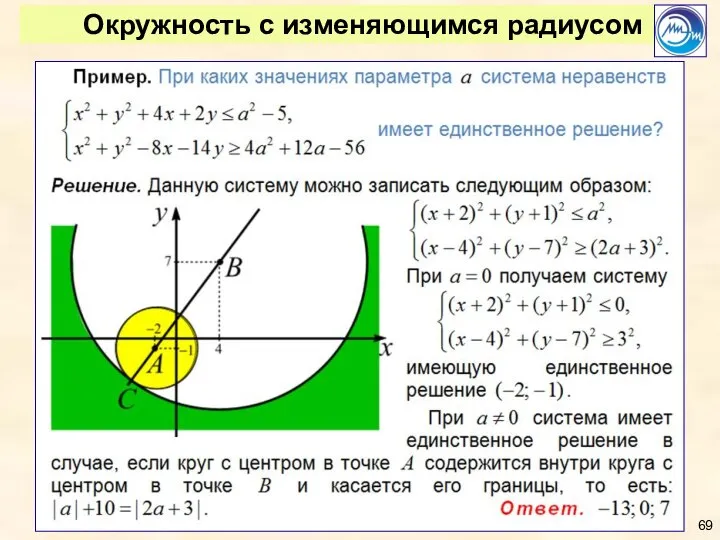
- 69. Окружность с изменяющимся радиусом
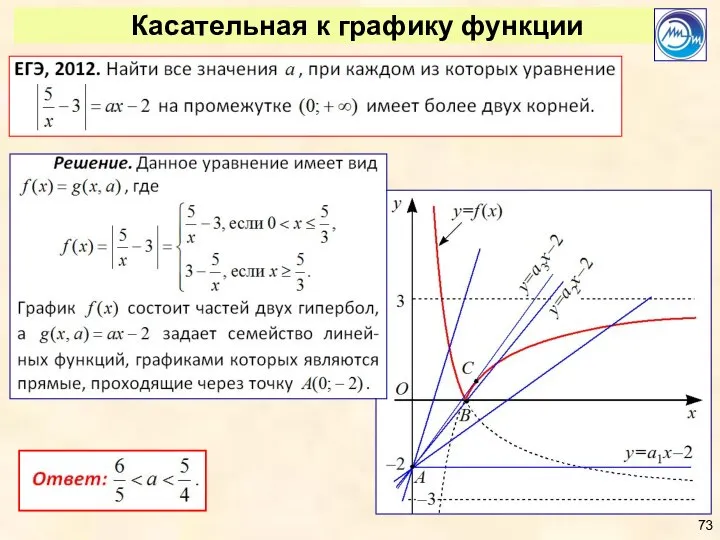
- 70. Касательная к графику функции (находится геометрически)
- 71. Касательная к графику функции
- 72. Касательная к графику функции
- 73. Касательная к графику функции
- 74. На помощь приходит производная
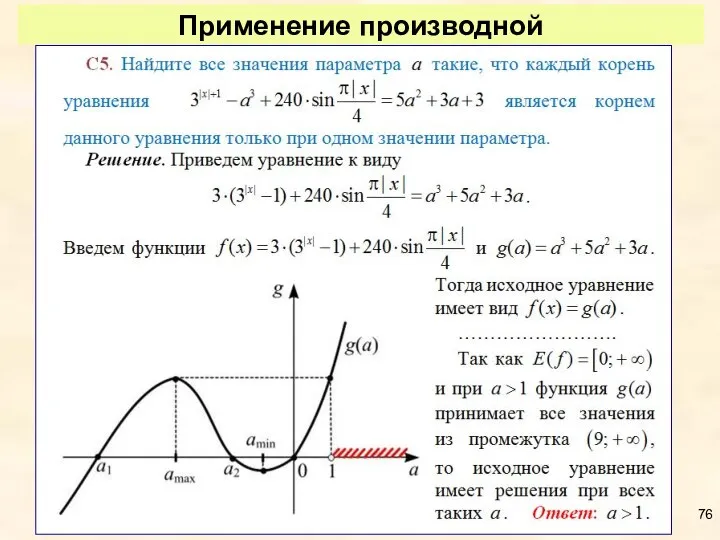
- 75. Применение производной
- 76. Применение производной
- 77. Печатные и электронные ресурсы Школьные учебники. Пособия для подготовки к ЕГЭ по математике. Журналы «Математика в
- 79. Скачать презентацию















































 История теоремы Пифагора
История теоремы Пифагора Несобственные интегралы
Несобственные интегралы Логарифмы
Логарифмы Логарифмы
Логарифмы Логарифмические неравенства
Логарифмические неравенства История системы мер длины (часть 1)
История системы мер длины (часть 1) Законы сложения и умножения
Законы сложения и умножения Применение производной. Учебно-тренировочные материалы для подготовки к ЕГЭ
Применение производной. Учебно-тренировочные материалы для подготовки к ЕГЭ Практическое. Занятие № 7. Численные методы решения задачи коши
Практическое. Занятие № 7. Численные методы решения задачи коши “Розв’язування задач”. Навчальний зошит. 2 клас. 3 частина
“Розв’язування задач”. Навчальний зошит. 2 клас. 3 частина Группируем слагаемые и множители
Группируем слагаемые и множители Треугольники
Треугольники Простейшие тригонометрические неравенства и методы их решения
Простейшие тригонометрические неравенства и методы их решения 6a639551ce27612e
6a639551ce27612e Математическая модель Память человека
Математическая модель Память человека Построение графиков функций
Построение графиков функций Распредели предметы поровну
Распредели предметы поровну Теория групп. Выкладывание мозаики
Теория групп. Выкладывание мозаики Применение производной к построению графиков функции
Применение производной к построению графиков функции Классная работа по математике
Классная работа по математике Презентация на тему Старинные меры длины
Презентация на тему Старинные меры длины  Угол между прямой и плоскостью
Угол между прямой и плоскостью Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе
Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе Подсчитай, сколько
Подсчитай, сколько Презентация на тему Свойства сложения (2 класс)
Презентация на тему Свойства сложения (2 класс)  uravnenie_urok_2
uravnenie_urok_2 Сходимость последовательности СВ
Сходимость последовательности СВ Множества
Множества