Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)

Март 1, 2021

Главная
Математика
Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)

Содержание

2. Т е ң с і з д і к т е р Сабақтың тақырыбы:
3. ах>b, ax Мұндағы a,b – кез келген бір сандар. х – айнымалы (белгісіз).
5. 4(х-3)+5х≥3х 4х-12+5х≥3х 4х+5х-3х≥12 6х≥12 х≥2 Жауабы: [2;+∞) немесе 2 ≥х
6. Анықтама: ах²+bх+с>0 , ах²+bх+с Мұндағы а≠0.
7. Теңсіздіктің шешімдер жиыны.
8. Бір айнымалысы бар екінші дәрежелі теңсіздікті шешу алгоритмі 1. Теңсіздікті ax2+bx+c>0 (ax2+bx+c 2. y=ax2+bx+c функциясын қарастырамыз
10. Скачать презентацию

Слайд 2

Т е ң с і з д і к т е р

Т е ң с і з д і к т е р Сабақтың тақырыбы:

Сабақтың тақырыбы:

Слайд 3

ах>b, axМұндағы a,b

ах>b, ax Мұндағы a,b – кез келген бір сандар. х – айнымалы (белгісіз).

– кез келген бір сандар.
х – айнымалы (белгісіз).

Слайд 4

Слайд 5

4(х-3)+5х≥3х
4х-12+5х≥3х
4х+5х-3х≥12
6х≥12
х≥2
Жауабы: [2;+∞) немесе 2 ≥х

4(х-3)+5х≥3х 4х-12+5х≥3х 4х+5х-3х≥12 6х≥12 х≥2 Жауабы: [2;+∞) немесе 2 ≥х

Слайд 6

Анықтама: ах²+bх+с>0 , ах²+bх+с<0, ах²+bх+с≥0 , ах²+bх+с≥0 түріндегі теңсіздіктер квадрат теңсіздіктер деп

Анықтама: ах²+bх+с>0 , ах²+bх+с Мұндағы а≠0.

аталады.
Мұндағы а≠0.

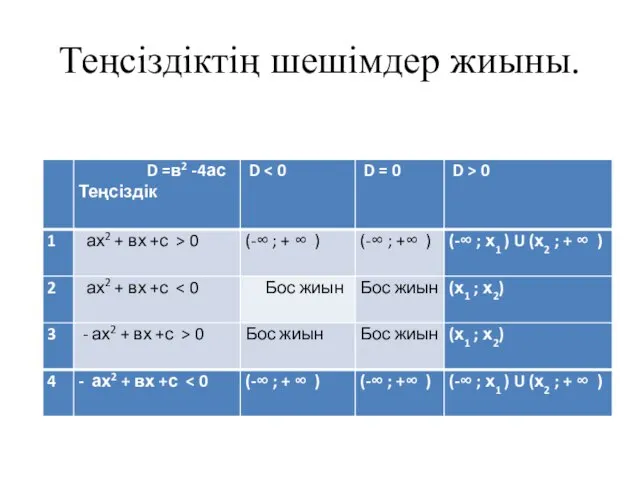
Слайд 7

Теңсіздіктің шешімдер жиыны.

Теңсіздіктің шешімдер жиыны.

Слайд 8

Бір айнымалысы бар екінші дәрежелі теңсіздікті шешу алгоритмі
1. Теңсіздікті ax2+bx+c>0 (ax2+bx+c<0) түріне

Бір айнымалысы бар екінші дәрежелі теңсіздікті шешу алгоритмі 1. Теңсіздікті ax2+bx+c>0 (ax2+bx+c

келтіру
2. y=ax2+bx+c функциясын қарастырамыз
3. Парабола тармақтарының бағытын анықтау
4. Параболаның ох осін қиятын нүктелерін анықтау (ax2+bx+c=0 теңдеуін шешіп; х1 және х2 табамыз
5. y=ax2+bx+c схемалық графигін саламыз
6. y>0 (y<0) болатындай параболаның бөлігін көрсетеміз
7. Абсцисса осінен y>0 (y<0) болатындай х-тің мәнін көрсетеміз
8. Аралықпен жауабын жазу