Статистика. Тренды

Тренды
Тренд (от англ. trend — тенденция) — это долговременная тенденция изменения исследуемого временного ряда.
Тренды могут быть описаны различными уравнениями — линейными, логарифмическими, степенными и так далее.
Методы оценки
Параметрические — рассматривают временной ряд как гладкую функцию При этом сначала выявляют один либо несколько допустимых типов функций, затем различными методами оценивают параметры этих функций, после чего на основе проверки критериев адекватности выбирают окончательную модель тренда.
Непараметрические — это разные методы сглаживания исходного временного ряда —скользящие средние (простая, взвешенная), экспоненциальное сглаживание. Они полезны в случае, когда для оценки тренда не удается подобрать подходящую функцию.

Анализ ряда данных
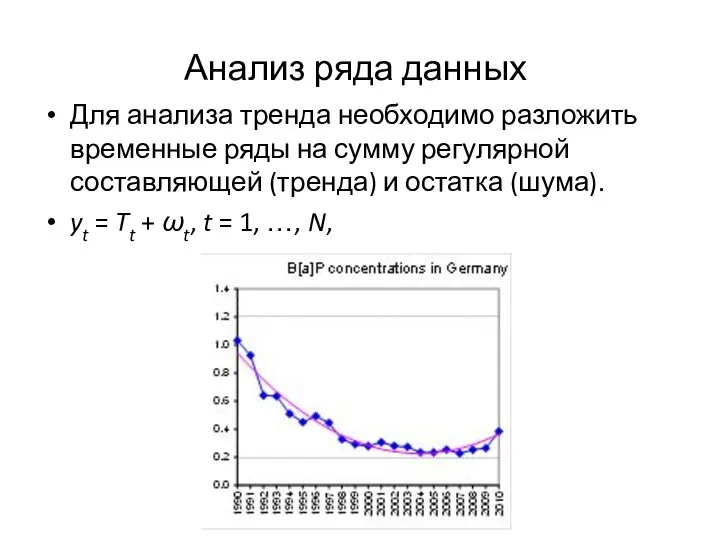
Для анализа тренда необходимо разложить временные ряды на сумму регулярной составляющей (тренда) и остатка (шума).
yt = Tt + ωt, t = 1, …, N,

Анализ ряда данных (продолжение)
Для анализа тренда временных рядов необходимо выполнить следующие шаги:
Шаг 1. Обнаружение тенденции и ее характер. На этом этапе нужно убедиться, что тренд существует и определяет характер тренда (увеличение, уменьшение или смешение).
Шаг 2. Идентификация типа тренда. На этом этапе следует выбрать тип тренда, подходящий для описания общих тенденций рассматриваемых временных рядов (например, линейного тренда, экспоненциального тренда и т. д.). Ниже приводятся возможные типы тенденций.
Шаг 3. Количественная оценка тренда. На этом этапе выполняется выбор основных параметров, описывающих тренд выбранного типа.
Шаг 4. Расчеты и интерпретация полученных результатов.

Тест Манна-Кендалла
Непараметрический тест для определения наличия монотонной, статистически значимой тенденции.
Для многолетних рядов данных без явно выраженных сезонных колебаний.
Для временных рядов с менее чем 10 значений используется S – статистика (Gilbert (1987)), для временных рядов от 10значений используется нормальное приближение (normal approximation) или Z статистика
Основан на статистике S или Z, рассчитанной как разность между возрастающими и уменьшающимися парами значений в исследуемом временном ряду

S-статистика Теста Манна-Кендалла
Если временной ряд состоит из 9 или менее значений то результаты расчета по формулам сравниваются непосредственно с теоретическим распределением, полученный Манном и Кендалом (Gilbert, 1987).
Полученные значения сравниваются с определенными табличными значениями и в результате подтверждается или опровергается нулевая гипотеза (гипотеза, что тренда нет).

Аппроксимационный тест (Z- статистика) Теста Манна-Кендалла
Для временного ряда из 10 и более значений.
Для проведения данной проверки рассчитывается S и ее дисперсия (с учетом возможности наличия «связанных» или «равных» значений).
Если вычисленное значение статистики Z превышает соответствующий порог по абсолютной величине, то предполагается, что серия имеет тенденцию на соответствующем уровне достоверности.

Метод Сенса
Использует линейную модель для оцени наклона тренда (т.е. в случаях, если предполагается что тренд линейный).
Распределение «остатков» предполагается постоянной во времени.
Не чувствителен к ошибочным значениям и «выбросам».
Для каждой пары рядом стоящих чисел рассчитывается угол наклона Qi.
Если в временном ряду есть n значений xj, мы получаем столько же, сколько N = n (n-1) / 2 оценок наклона Qi.
Оценкой склона Сена является медиана этих N значений Qi. Значения N Qi оцениваются от
наименьшего до самого большого

Анализ ряда данных с явно выраженной сезонной составляющей (один из методов)
Тренд (Tt) можно разложить на несколько компонентов тренда, описывающих разные типы поведения исследуемых величин(yt) во времени, например «основной» тренд и сезонную составляющую.
C = Cmain + Cseas + ω,
Cmain,t = a1 · exp(- t / τ1) + a2 · exp(- t / τ2), (15)
Cseas,t = a1 · exp(- t / τ1) · (b11 · cos(2π · t – φ11) + b12 · cos(4π · t – φ12) + ...) + a2 · exp(- t / τ2) · (b21 · cos(2π · t – φ21) + b22 · cos(4π · t – φ22) + ...).
Ct = a1 · exp(- t / τ1) · (1 + b11 · cos(2π · t – φ11) + b12 · cos(4π · t – φ12) + ...)
+ a2 · exp(- t / τ2) · (1 + b21 · cos(2π · t – φ21) + b22 · cos(4π · t – φ22) + ...) + ωt,

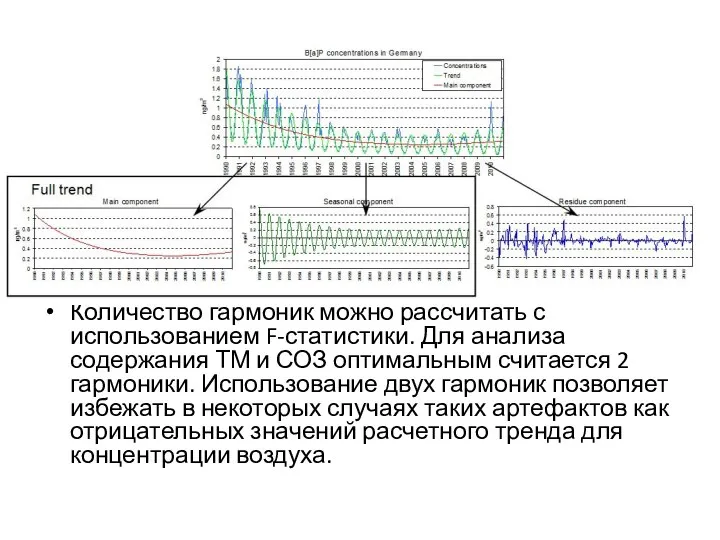
Количество гармоник можно рассчитать с использованием F-статистики. Для анализа содержания ТМ и СОЗ оптимальным считается 2 гармоники. Использование двух гармоник позволяет избежать в некоторых случаях таких артефактов как отрицательных значений расчетного тренда для концентрации воздуха.

Пример Количественной оценки тренда
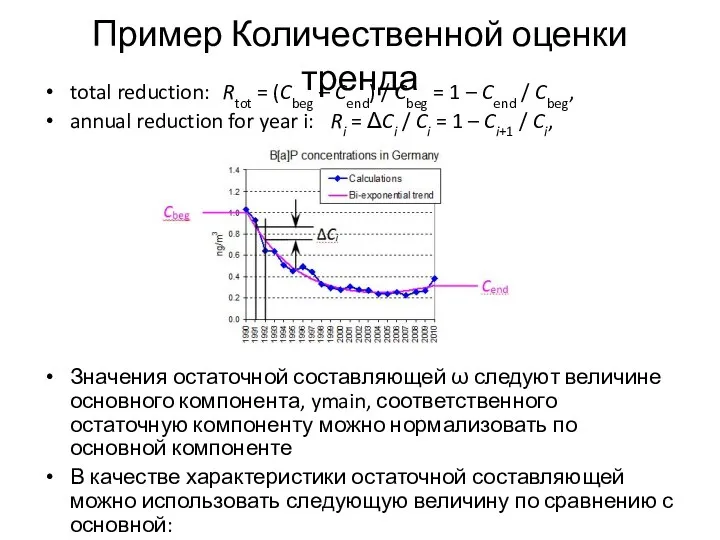
total reduction: Rtot = (Cbeg – Cend) / Cbeg = 1 – Cend / Cbeg,
annual reduction for year i: Ri = ΔCi / Ci = 1 – Ci+1 / Ci,
Значения остаточной составляющей ω следуют величине основного компонента, ymain, соответственного остаточную компоненту можно нормализовать по основной компоненте
В качестве характеристики остаточной составляющей можно использовать следующую величину по сравнению с основной:
Fres = σ(ωt / ymain,t)

Нормальное (Гаусса) распределение
это функция, которая описывает тенденцию высокой концентрации значений около центра
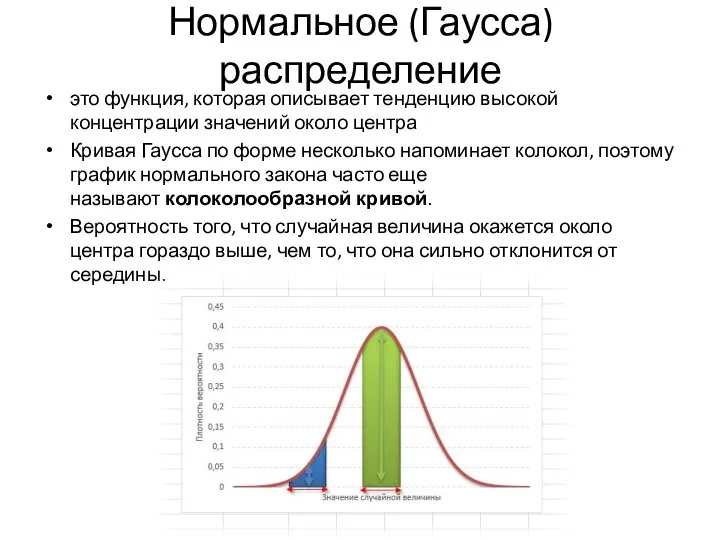
Кривая Гаусса по форме несколько напоминает колокол, поэтому график нормального закона часто еще называют колоколообразной кривой.
Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.

Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ2 характеризует размах вариации, то есть «размазанность» данных.

Правило трёх сигм
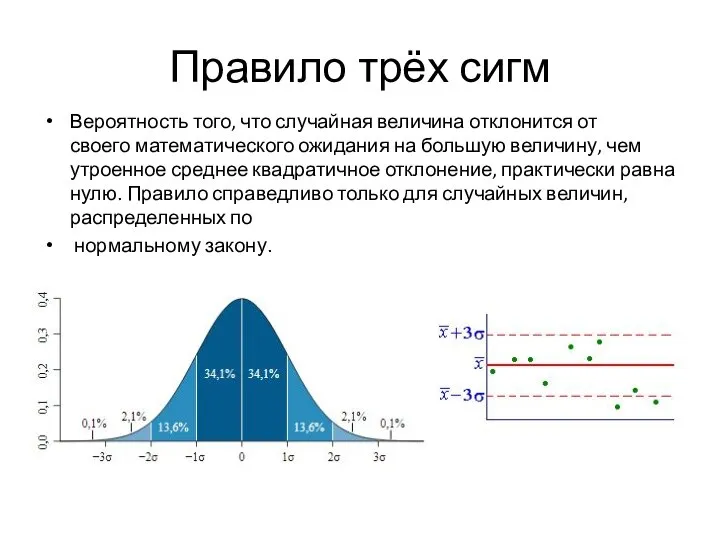
Вероятность того, что случайная величина отклонится от своего математического ожидания на большую величину, чем утроенное среднее квадратичное отклонение, практически равна нулю. Правило справедливо только для случайных величин, распределенных по
нормальному закону.

Логнормальное распределение
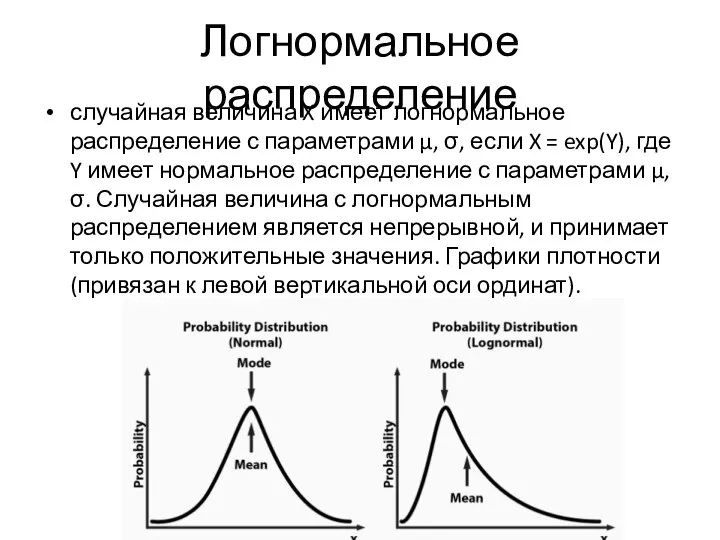
случайная величина X имеет логнормальное распределение с параметрами μ, σ, если X = exp(Y), где Y имеет нормальное распределение с параметрами μ, σ. Случайная величина с логнормальным распределением является непрерывной, и принимает только положительные значения. Графики плотности (привязан к левой вертикальной оси ординат).

Оценка показателя повторяемости методики анализа
Рассчитывают среднее арифметическое и выборочную дисперсию результатов единичного анализа содержания компонента, полученных в условиях повторяемости (параллельных определений).

Критерий Кохрена
Рассчитывается для выборки и сравнивается с табличными значениями. Если рассчитанного значение выше табличного, то соответствующая дисперсия исключается из дальнейшего расчета.
Не исключенные из расчетов дисперсии считают однородными и по ним оценивают средние квадратические отклонения, характеризующие повторяемость результатов единичного анализа (параллельных определений).

Оценка показателя правильности методики анализа
Рассчитывают значение смещения - как разность между средним значением результатов анализа , и аттестованным значением.
Далее проверяют значимость вычисленных значений по критерию Стьюдента.