Угол между прямыми

Цели и задачи урока:
Сформировать понятие угла между:
Пересекающимися;
Параллельными;
скрещивающимися прямыми.
Научиться находить угол между:
Пересекающимися;
параллельными ;
скрещивающимися прямыми.

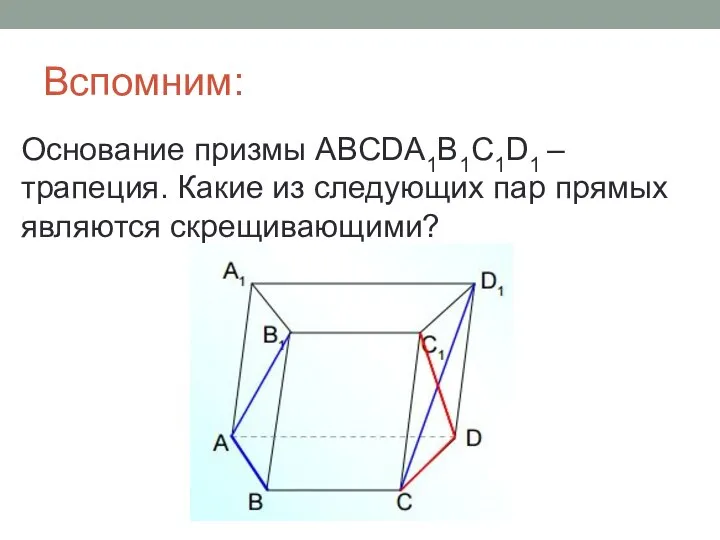
Вспомним:
Основание призмы ABCDA1B1C1D1 – трапеция. Какие из следующих пар прямых являются скрещивающими?

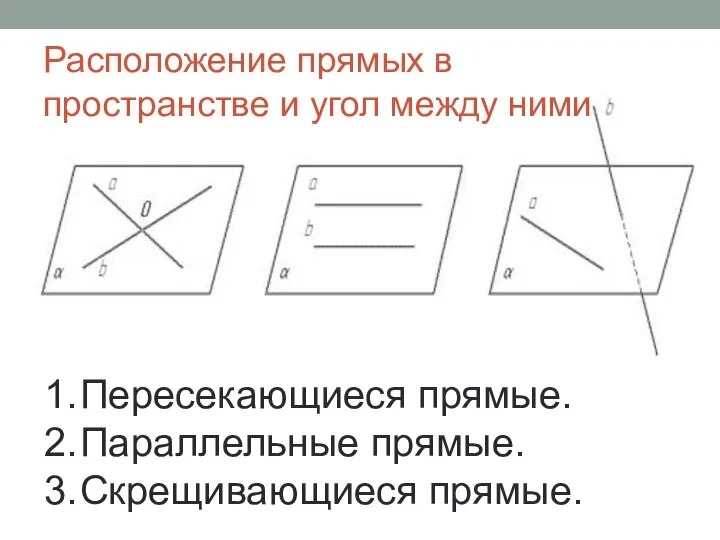
Расположение прямых в пространстве и угол между ними
1. Пересекающиеся прямые.
2. Параллельные прямые.
3. Скрещивающиеся прямые.

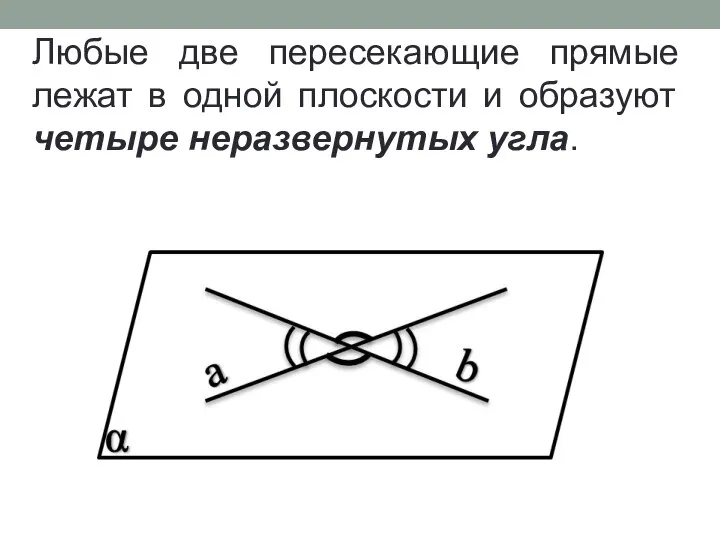
Любые две пересекающие прямые лежат в одной плоскости и образуют четыре неразвернутых угла.

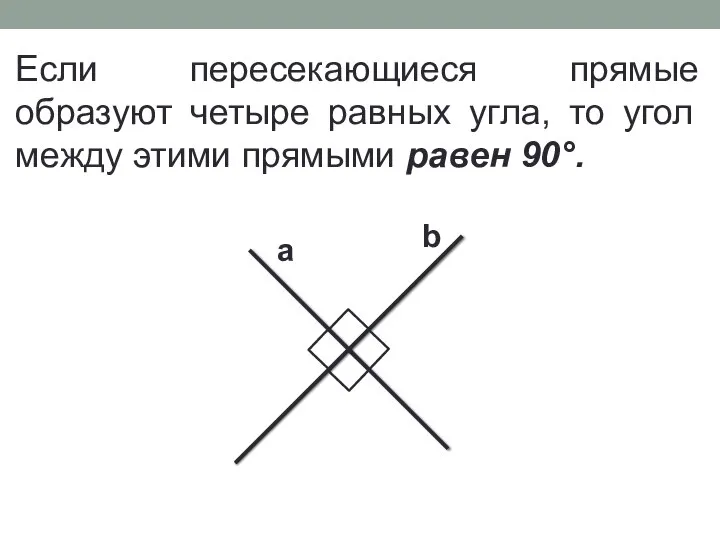
Если пересекающиеся прямые образуют четыре равных угла, то угол между этими прямыми равен 90°.
а
b

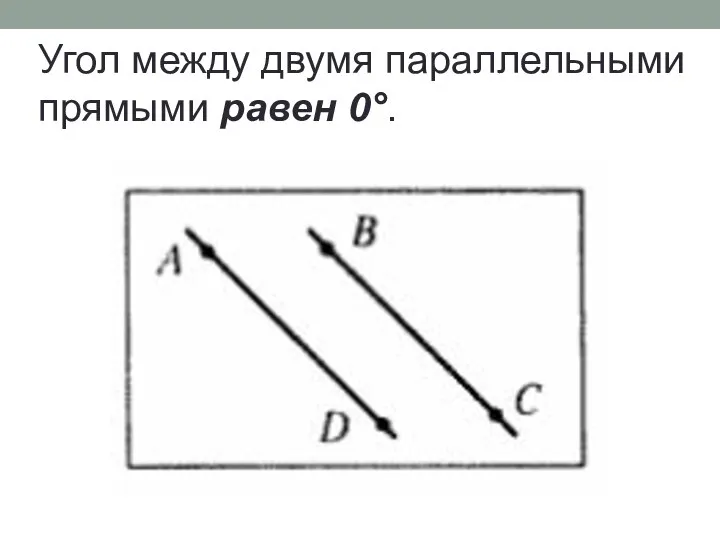
Угол между двумя параллельными прямыми равен 0°.

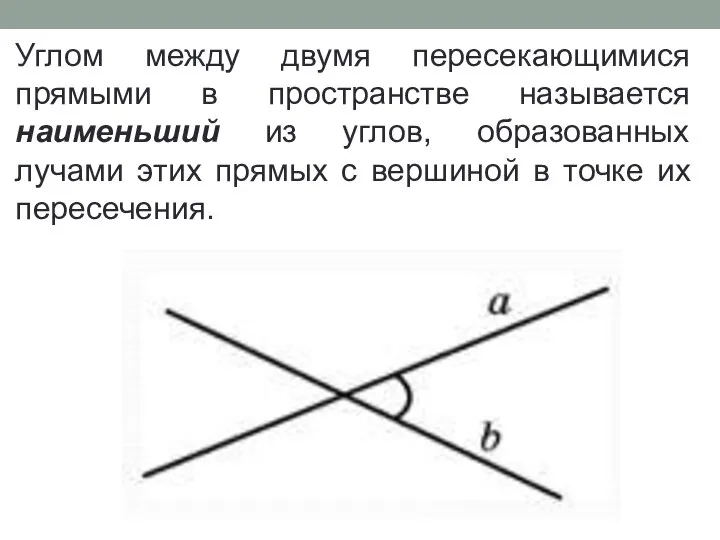
Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения.

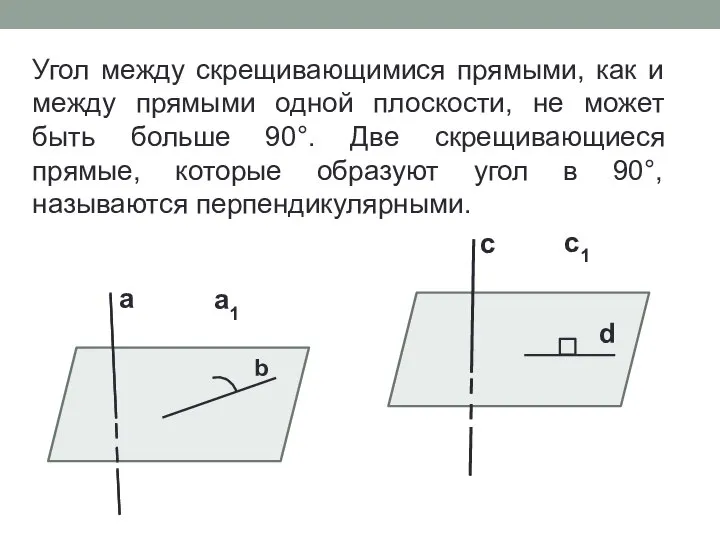
Угол между скрещивающимися прямыми, как и между прямыми одной плоскости, не может быть больше 90°. Две скрещивающиеся прямые, которые образуют угол в 90°, называются перпендикулярными.
a
b
a1
c
c1
d

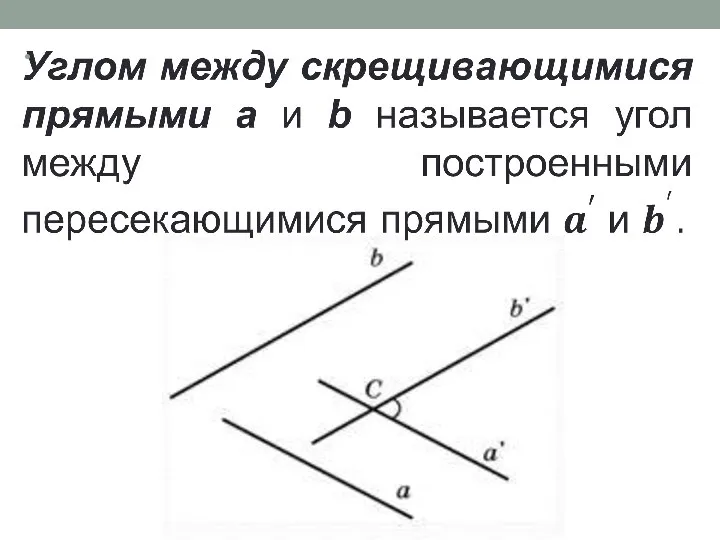
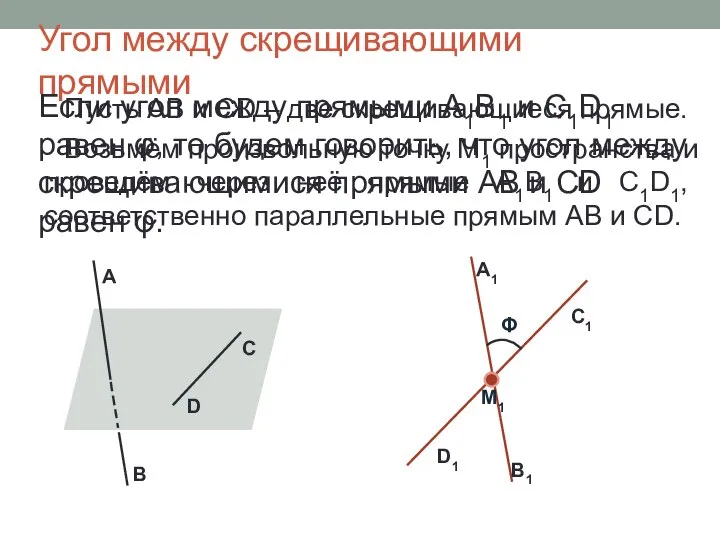
Угол между скрещивающими прямыми
Пусть AB и CD – две скрещивающиеся прямые.
Возьмём произвольную точку М1 пространства и проведём через неё прямые А1В1 и C1D1, соответственно параллельные прямым AB и CD.
M1
Φ
Если угол между прямыми А1В1 и C1D1 равен φ, то будем говорить, что угол между скрещивающимися прямыми АВ и CD равен φ.

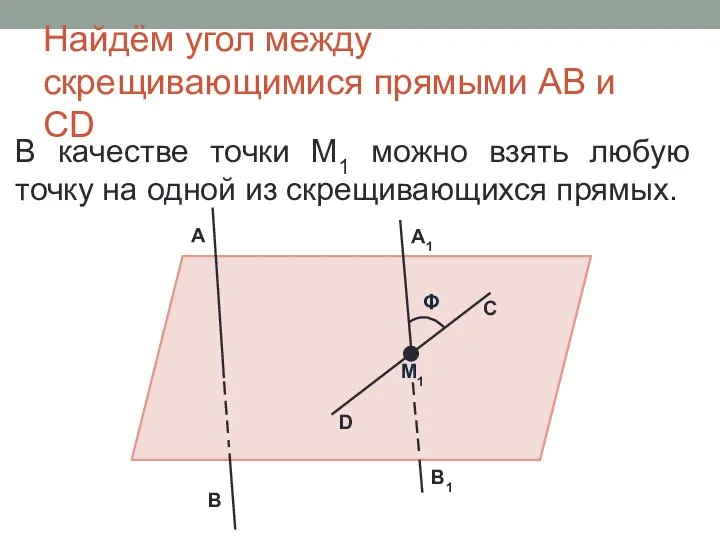
Найдём угол между скрещивающимися прямыми AB и CD
В качестве точки M1 можно взять любую точку на одной из скрещивающихся прямых.
M1
Φ

Физкультминутка
для глаз

Покажите перпендикулярные скрещивающиеся прямые в окружении.

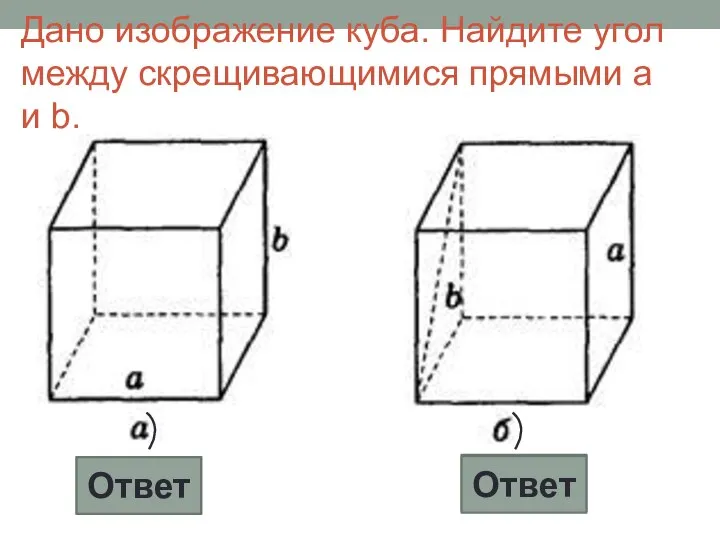
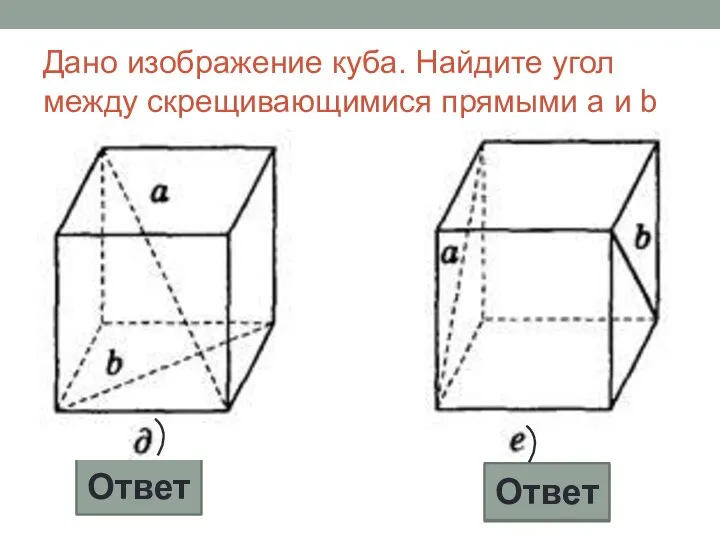
Дано изображение куба. Найдите угол между скрещивающимися прямыми а и b.
90°
45°
Ответ
Ответ

Дано изображение куба. Найдите угол между скрещивающимися прямыми а и b.
90°
60°
Ответ
Ответ

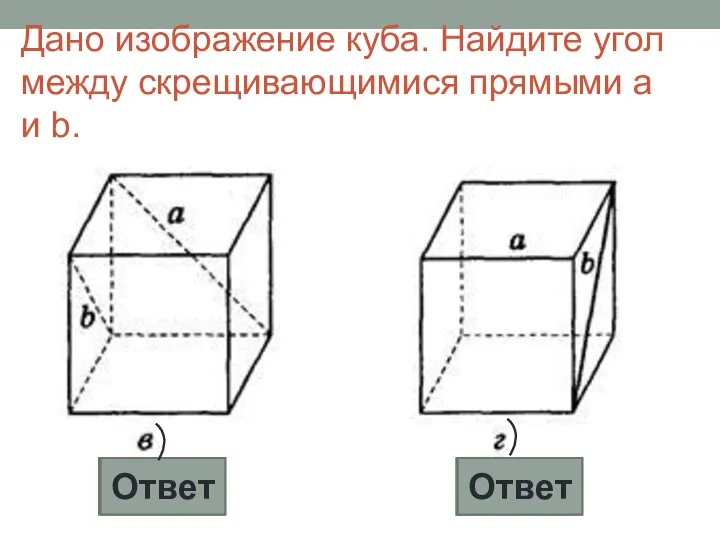
Дано изображение куба. Найдите угол между скрещивающимися прямыми а и b
90°
90°
Ответ
Ответ

Домашнее задание:
§4 (стр. 85-89), №268, №269.

Физкультминутка

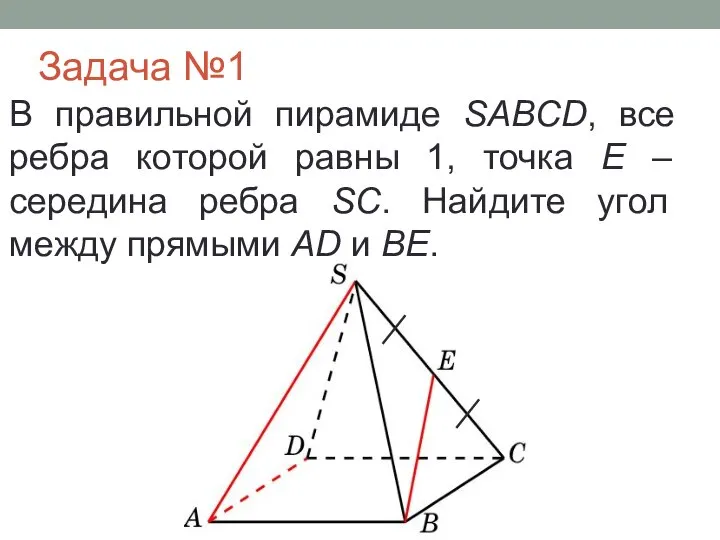
Задача №1
В правильной пирамиде SABCD, все ребра которой равны 1, точка E – середина ребра SC. Найдите угол между прямыми AD и BE.