Теорема Пифагора

Пифагор Самосский (др.-греч. Πυθαγόρας ὁ Σάμιος, лат. Pythagoras; 570—490 гг. до н. э.) — древнегреческий
философ, математик имистик, создатель религиозно-философской школы
пифагорейцев.

Пифагор на фреске
Рафаэля
(1509 г.)

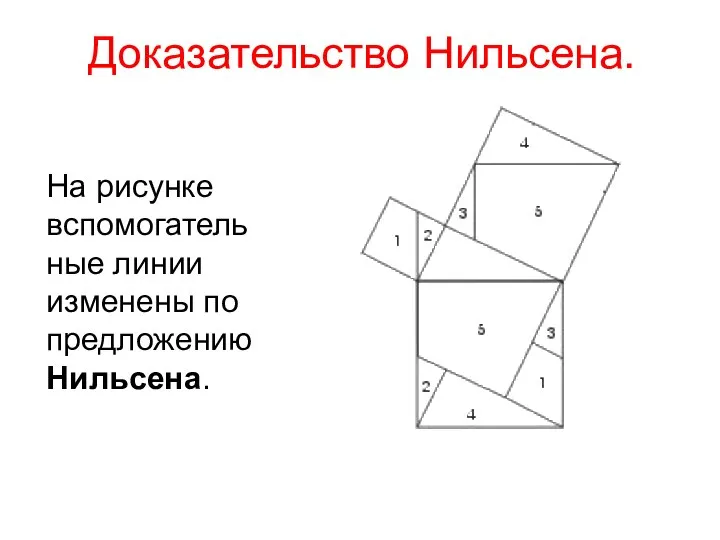
Доказательство Нильсена.
На рисунке вспомогательные линии изменены по предложению Нильсена.

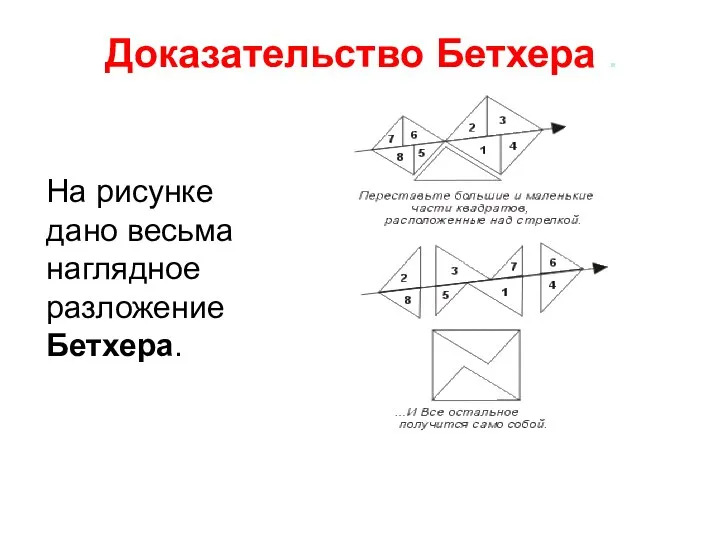
Доказательство Бетхера .
На рисунке дано весьма наглядное разложение Бетхера.

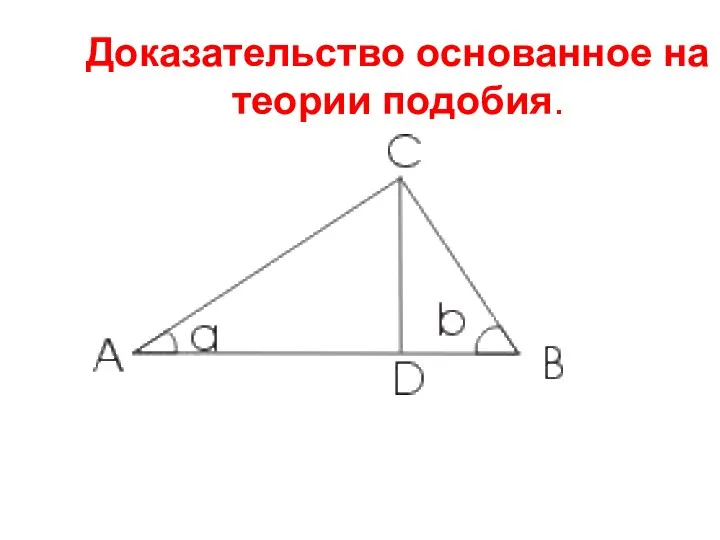
Доказательство основанное на теории подобия.

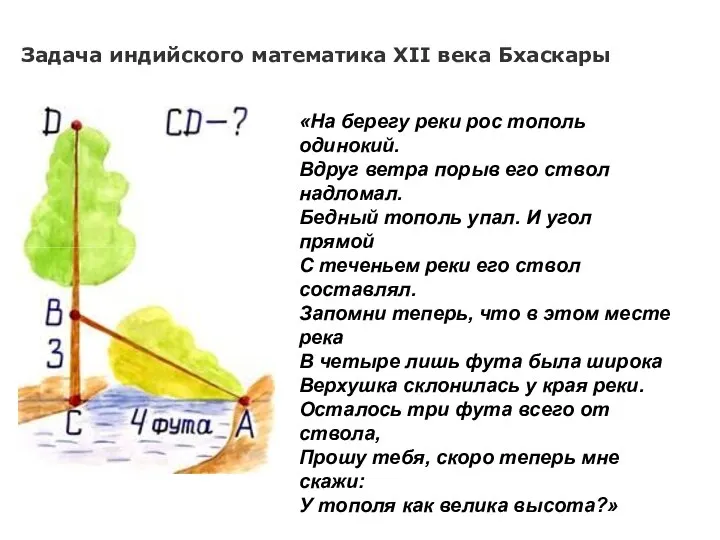
Задача индийского математика XII века Бхаскары
«На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»

Задача о лотосе
из сочинения Бхаскары (XII век)
На стебле с полфута над озером
тихим,
Рос лотоса цвет.
Он рос одиноко. И ветер порывом
Отнёс его в сторону. Нет
Больше цветка над водой.
Нашёл же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода здесь глубока?
Ответ: 3,75

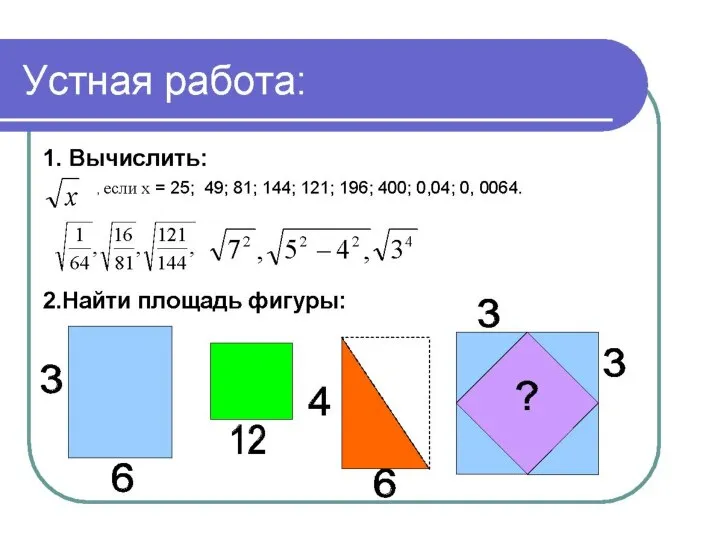
Значение теоремы Пифагора
Из теоремы Пифагора или с её помощью можно вы-
вести большинство теорем геометрии.
Она позволяет
1)Находить стороны прямоугольника;
2)Строить прямые углы;
3) Строить отрезки с иррациональными длинами;
4) Не проводя линии, можно узнать ее длину;)
Благодаря этой теореме мы можем находить расстояние между точками, не измеряя этого расстояния непосредственно, даже не рассматривая прямую, проходящую между этими точками)

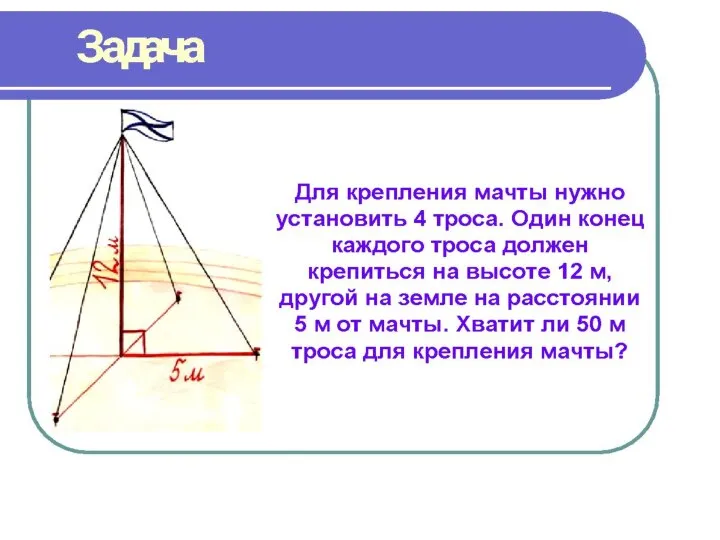
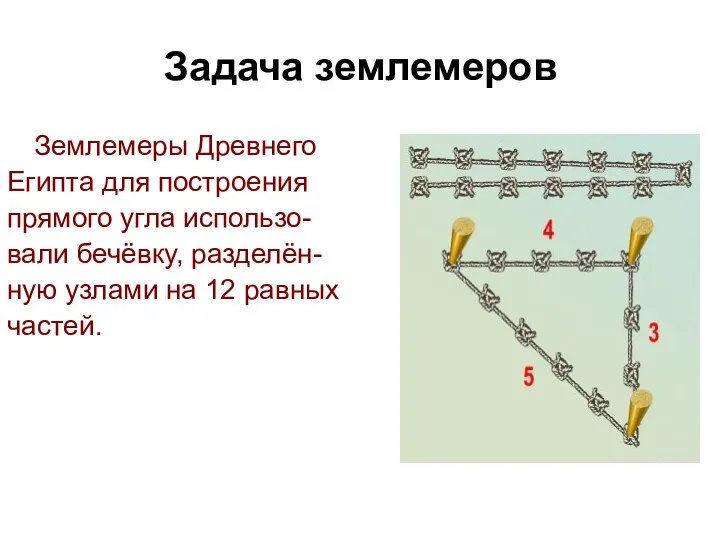
Задача землемеров
Землемеры Древнего
Египта для построения
прямого угла использо-
вали бечёвку, разделён-
ную узлами на 12 равных
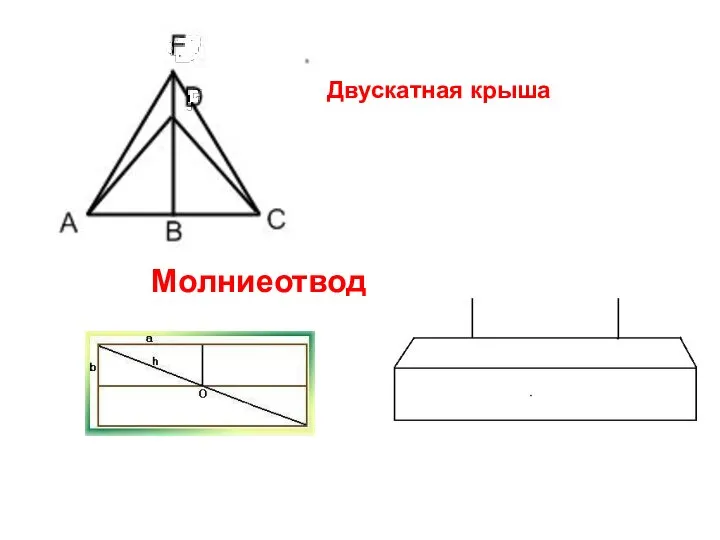
частей.

Двускатная крыша
Молниеотвод

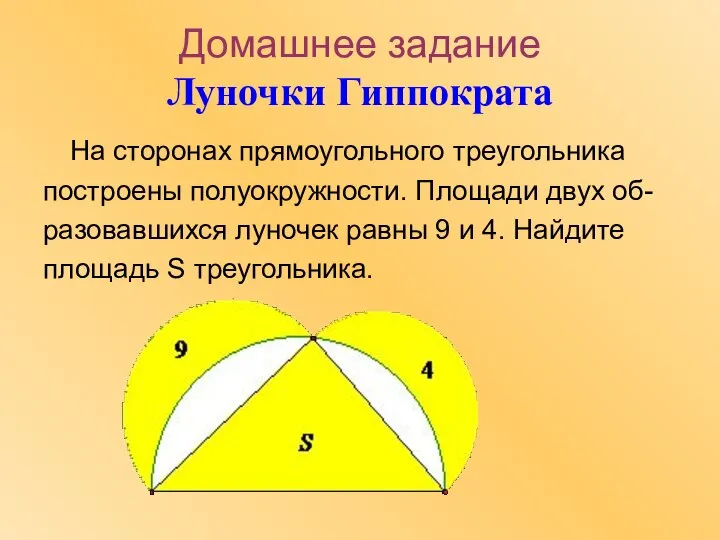
Домашнее задание
Луночки Гиппократа
На сторонах прямоугольного треугольника
построены полуокружности. Площади двух об-
разовавшихся луночек равны 9 и 4. Найдите
площадь S треугольника.